Мультиплікативна модель тимчасового ряду

Рис. 3.

Рис. 2.

Рис. 1.

Адитивна модель тимчасового ряду.

При побудові эконометричної моделі використовуються два типи даних:

1) дані, що характеризують сукупність різних об'єктів у визначений момент часу;

2) дані, що характеризують один об'єкт за ряд послідовних моментів часу.

Моделі, побудовані за даними першого типу, називаються просторовими моделями. Моделі, побудовані на основі другого типу даних, називаються моделями тимчасових рядів.

Часовий ряд (ряд динаміки) – це сукупність значень якого-небудь показника за кілька послідовних моментів або періодів часу. Кожен рівень тимчасового ряду формується під впливом великого числа факторів, що умовно можна підрозділити на три групи:

1) фактори, що формують тенденцію ряду;

2) фактори, що формують циклічні коливання ряду;

3) випадкові фактори.

Розглянемо вплив кожного фактора на часовий ряд окремо.

Більшість тимчасових рядів економічних показників мають тенденцію, що характеризує сукупний довгостроковий вплив безлічі факторів на динаміку досліджуваного показника. Усі ці фактори, узяті окремо, можуть робити різнонаправлений вплив на досліджуваний показник. Однак у сукупності вони формують його зростаючу або убутну тенденцію. На мал. 9.1 показаний гіпотетичний часовий ряд, що містить зростаючу тенденцію.

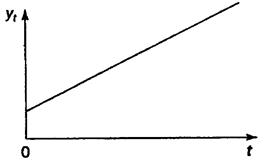
Також досліджуваний показник може бути підданий циклічним коливанням. Ці коливання можуть носити сезонний характер, оскільки економічна діяльність ряду галузей економіки залежить від часу року (наприклад, ціни на сільськогосподарську продукцію в літній період вище, ніж у зимовий; рівень безробіття в курортних містах у зимовий період вище в порівнянні з літнім). При наявності великих масивів даних за тривалі проміжки часу можна виявити циклічні коливання, зв'язані з загальною динамікою кон'юнктури ринку. На рис. 2 представлений гіпотетичний часовий ряд, що містить тільки сезонну компоненту.

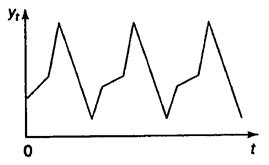
Деякі тимчасові ряди не містять тенденції і циклічної компоненти, а кожен наступний їхній рівень утворюється як сума середнього рівня ряду і якоїсь (позитивної або негативної) випадкової компоненти. Приклад ряду, що містить тільки випадкову компоненту, приведений на рис. 3.

Очевидно, що реальні дані не випливають цілком і цілком з яких-небудь описаних вище моделей. Найчастіше вони містять усі три компоненти. Кожен їхній рівень формується під впливом тенденції, сезонних коливань і випадкової компоненти.

У більшості випадків фактичний рівень тимчасового ряду можна представити як суму або добуток трендової, циклічної і випадкової компонентів. Модель, у якій часовий ряд представлений як сума перерахованих компонентів, називається аддитивною моделлю тимчасового ряду. Модель, у якій часовий ряд представлений як добуток перерахованих компонентів, називається мультиплікативною моделлю тимчасового ряду. Основна задача эконометричного дослідження окремого тимчасового ряду – виявлення і додання кількісного виразу кожної з перерахованих вище компонентів для того, щоб використовувати отриману інформацію для прогнозування майбутніх значень ряду або при побудові моделей взаємозв'язку двох або більш тимчасових рядів.

Ми будемо розглядати моделі лінійного тренду, тобто параметри тренда можливо розрахувати за допомогою моделі лінійної регресії.

Спочатку на основі минулих даних знаходимо сезонну варіацію. Виключив сезонну варіацію за допомогою лінійної регресії знаходимо рівняння тренду. По рівнянню тренда та минулих даних обчислюємо величини похибок. Це середнє абсолютне відхилення MAD=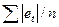та середньоквадратична похибка МSE=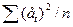, де e_t - це різниця між фактичними та прогнозними даними в момент часу t, n – кількість даних спостережень.

Для адитивної моделі тимчасового ряду маємо: фактичне значення А= трендові значення Т + сезонна варіація S + похибка Е.

Для мультиплікативної моделі тимчасового ряду маємо: фактичне значення А= трендові значення Т х сезонна варіація S х похибка Е.

Побудова аддитивной і мультиплікативної моделей зводиться до розрахунку значень 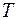, 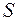і 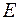для кожного рівня ряду.

Процес побудови моделі містить у собі наступні кроки.

1) Вирівнювання вихідного ряду методом ковзної середньої.

2) Розрахунок значень сезонної компоненти .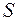

3) Усунення сезонної компоненти з вихідних рівнів ряду й одержання вирівняних даних (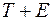) в адитивній або (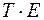) у мультиплікативній моделі.

4) Аналітичне вирівнювання рівнів (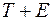) або (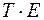) і розрахунок значень 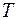з використанням отриманого рівняння тренда.

5) Розрахунок отриманих по моделі значень (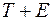) або ().

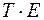6) Розрахунок абсолютних і відносних помилок. Якщо отримані значення помилок не містять автокореляції, ними можна замінити вихідні рівні ряду і надалі використовувати часовий ряд помилок 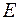для аналізу взаємозв'язку вихідного ряду й інших тимчасових рядів.

Автокореляція в залишках може бути викликана декількома причинами, що мають різну природу.

1. Вона може бути зв'язана з вихідними даними і викликана наявністю помилок виміру в значеннях результативної ознаки.

2. У ряді випадків автокореляція може бути наслідком неправильної специфікації моделі. Модель може не включати фактор, що впливає на результат і вплив якого відбиває в залишках, унаслідок чого останні можуть виявитися автокорельованими. Дуже часто цим фактором є фактор часу .

Від щирої автокореляції залишків варто відрізняти ситуації, коли причина автокореляції полягає в неправильній специфікації функціональної форми моделі. У цьому випадку варто змінити форму моделі, а не використовувати спеціальні методи розрахунку параметрів рівняння регресії при наявності автокореляції в залишках.

Один з більш розповсюджених методів визначення автокореляції в залишках – це розрахунок критерію Дарбина-Уотсона:

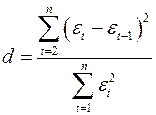. (1)

Т.е. величина 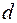є відношення суми квадратів разностей послідовних значень залишків до залишкової суми квадратів по моделі регресії.

Можна показати, що при великих значеннях 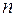існує наступне співвідношення між критерієм Дарбина-Уотсона 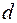і коефіцієнтом автокореляції залишків першого порядку :

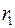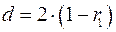. (2)

Таким чином, якщо в залишках існує повна позитивна автокореляція і 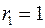, те 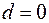. Якщо в залишках повна негативна автокореляція, то 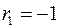і, отже, 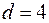. Якщо автокореляція залишків відсутній, то і 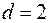. Тобто .

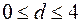Алгоритм виявлення автокореляції залишків на основі критерію Дарбина-Уотсона наступний. Висувається гіпотеза 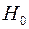про відсутність автокореляції залишків. Альтернативні гіпотези 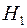і 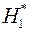складаються, відповідно, у наявності позитивної або негативної автокореляції в залишках. Далі по спеціальних таблицях визначаються критичні значення критерію Дарбина-Уотсона 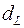і 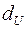для заданого числа спостережень 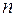, числа незалежних перемінні моделі 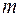і рівня значимості 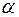. За цими значеннями числовий проміжок 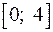розбивають на п'ять відрізків. Прийняття або відхилення кожної з гіпотез з імовірністю 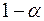здійснюється в такий спосіб:

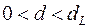– є позитивна автокореляція залишків, 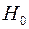відхиляється, з імовірністю 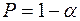приймається ;

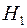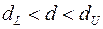– зона невизначеності;

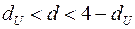– немає основ відхиляти 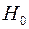, тобто автокореляція залишків відсутній;

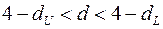– зона невизначеності;

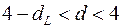– є негативна автокореляція залишків, 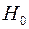відхиляється, з імовірністю 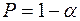приймається .

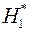Якщо фактичне значення критерію Дарбіна-Уотсона попадає в зону невизначеності, то на практиці припускають існування автокореляції залишків і відхиляють гіпотезу .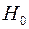

3. Експоненційне згладжування тимчасових рядів.

При аналізі часових рядів ми використовували метод ковзаної середньої, де усі дані (і піздні, і ранні) були рівноправні. Більш правильнимпредставляється спосіб, в якому даним приписують вагу: більш пізнім даним придається більшу вагу, чим більш ранім.

Дата добавления: 2013-12-13