Характеристики форми розподілу

Однорідність сукупності — це передумова використання інших статистичних методів (середніх величин, регресійного аналізу тощо). Однорідними вважаються такі сукупності, елементи яких мають спільні властивості (риси) і належать до одного типу, класу. При цьому однорідність означає не повну тотожність рис і властивостей елементів, а лише наявність у них загального в істотному, головному.

Формою розподілу статистичної сукупності прийнято називати криву співвідношення частот і значень варіюючої ознаки. Різноманітність статистичних сукупностей — передумова різних форм співвідношення частот і варіюючої ознаки. За своєю формою розподіли поділяють на такі види: одно-, дво- і багатовершинні. Наявність двох і більше вершин свідчить про неоднорідність сукупності, про поєднання в ній груп із різними рівнями ознаки. Розподіли якісно однорідних сукупностей, як правило, одновершинні. Серед одновершинних розподілів є симетричні і асиметричні (скошені), гостро- і плоско вершинні.

У симетричному розподілі рівновіддалені від центру значення ознаки мають однакові частоти, а в асиметричному — вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена вліво, то це правостороння асиметрія, і навпаки.

200

Найпростішою мірою асиметрії є відхилення між середньою арифметичною, модою і медіаною. В симетричному розподілі характеристики центру мають однакові значення = Ме = Мо _; в асиметричному між ними існують певні розбіжності. При правосторонній асиметрії > Ме>Мо, при лівосторонній, навпаки < Ме < Мо.

Асиметрія як відносна статистична характеристика дорівнює різниці між середнім значенням і медіаною або модою, поділеними на середнє квадратичне відхилення.

Стандартизовані відхилення 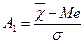, або

характеризують напрям і міру скошеності розподілу. Очевидно, що в симетричному розподілі А = 0, при правосторонній асиметрії А > 0, при лівосторонній А < 0.

Розрахунок стандартизованих відхилень середньої і медіани, середньої та моди розглянемо на прикладі (табл. 6.7):

Таблиця 6.7. Розподіл робітників підприємства за стажем роботи

Стаж роботи, років	Кількість робітників f	Кумулятивна частка Sf	Центр інтервалу хі	хf	х^2f
До 5
5-7
7-9
9-11
11-13
13-15
15 і більше
Разом		-	-

За даними таблиці обчислюємо:

1. Середній стаж роботи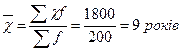

2. Медіана стажу роботи

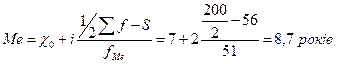
3. Мода стажу роботи

4. Середнє квадратичне відхилення

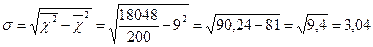
5. Стандартизовані відхилення

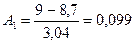
Обчислені показники свідчать про помірну правосторонню асиметрію розподілу.

У симетричних та помірно асиметричних розподілах вимірюється ексцес розподілу.

Асиметрія та ексцес — це дві пов'язані з варіацією властивості форми розподілу. Комплексна їх оцінка виконується на основі центральних моментів розподілу. Алгебраїчно центральний момент розподілу — це середня арифметична k -го ступеня відхилення індивідуальних значень ознаки від середньої:

Очевидно, що момент 2-го порядку є дисперсією, яка характеризує варіацію. Моменти 3-го і 4-го порядку характеризують відповідно асиметрію та ексцес. У симетричному розподілі μ₃ = 0. Чим більша скошеність ряду, тим більше значення μ₃. Для того, щоб характеристика скошеності не залежала від масштабу вимірювання ознаки, для порівняння ступеня асиметрії різних розпо­ділів використовується стандартизований момент А_S = μ₃:σ³. При правосторонній асиметрії коефіцієнт А_S > 0, при лівосторонній А_S < 0. Звідси правостороння асиметрія називається додатньою, а лівостороння — від'ємною. Вважається, що при А_S < 0,25 асиметрія низька, якщо А_S не перевищує 0,5 — середня, при А_S > 0,5 — висока.

Для вимірювання ексцесу використовується стандартизований момент 4-го порядку Е_к = μ₃:σ⁴. У симетричному, близькому до нормального розподілі Е_к = 3. Очевидно, при гостровершинному розподілі Е_к > 3, при плосковершинному Е_к < 3.

Порядок обчислення коефіцієнтів асиметрії і ексцесу розглянемо на прикладі (табл. 6.8):

Таблиця 6.8. Розрахунок коефіцієнтів асиметрії та ексцесу
Урожайність озимої пшениці, ц/га	Посівна площа, % f	χі	χf
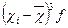
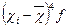
1	2	3	4	5	6	7	8	9
40-42 42-44 44-46 46-48 48-50 50-52 52-54			1 260 1 645	-5,72 -3,72 -1,72 0,28 2,28 4,28 6,28	32,7 184 13,8 384 2,9 584 0,0 784 5,1 984 18,3 184 39,4 384	130,8 736 96,8 688 82,8 352 2,744 83,1 744 109,3 104 157,7 536	-748,5 970 -360,3 519 -142,4 765 0,7 683 189,6 376 470,4 165 990,6 926	4 281,975 1 340,509 245,060 0,215 432,374 2 013,383 6 221,550
Разом			4 672			664,16	400,0 896	14 535,066

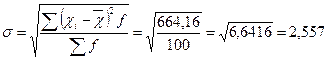
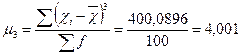
А_S = μ₃: σ³ = 4,00і: 2,577³ = 0,2 337

Е_k = μ₄: σ⁴ = і45,35і: 2,577⁴ = 3,2 95і

Отже, розподіл посівних площ за врожайністю озимої пшениці характеризується незначною правосторонньою асиметрією. Коефіцієнт ексцесу більший за 3 (Е_к=3,2951), що свідчить про гостровершинність розподілу (рис. 6.1).

Дата добавления: 2013-12-14