Генеральної і вибіркової сукупностей

Характеристика	Сукупність
генеральна	вибіркова
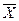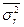Обсяг сукупності   Середнє значення ознаки   Загальна дисперсія   Середня з групових дисперсій   Міжгрупова дисперсія   Частка елементів сукупності, які мають певні значення ознаки Частка вибіркової сукупності в генеральній Кількість серій Дисперсія альтернативної ознаки	N     σr^2     δr^2   W 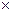R σr^2=pg	n 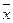    σ^2 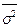    δ^2   w D R σ^2=w(і-w)

Достовірність вибіркового спостереження забезпечується розрахунками його помилок для середньої величини і для частки (питомої ваги) ознаки, що вивчається. Помилки вибірки (репрезентативності) позначаються символом (дельта) і є різницею між вибірковою середньою (часткою) і генеральною середньою (часткою):

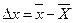- помилка вибірки для середньої величини

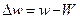- помилка вибірки для частки.

Ці помилки складаються з помилок репрезентативності і помилок реєстрації. Величини помилок вибірки (репрезентативності) в основному залежить:

по-перше, від обсягу вибірки, тому що зі збільшенням числа досліджуваних одиниць результати вибірки все менше будуть відрізнятися від результатів генеральної сукупності;

по-друге, від варіації досліджуваної ознаки. Чим більше варіює ознака, тим більше вибіркова середня (частка) відрізняється від генеральної середньої (частки). Оскільки основним показниками варіації ознаки є дисперсія і середнє квадратичне відхилення, то можна стверджувати, що помилка вибірки перебуває у прямій залежності від величин цих показників;

по-третє, від способу і виду відбору вибіркової сукупності.

Для узагальнюючої характеристики помилок репрезентативності розраховують середню помилку вибірки μ, її називають ще стандартом. Для визначення середньої помилки репрезентативності вибірки застосовують формули (табл. 7.2):

Таблиця 7.2. Середня помилка вибірки

Спосіб відбору	Метод відбору
повторний	безповторний
помилка вибрки для середньої величини
Випадковий і механічний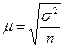
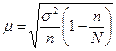
Типовий (районований)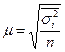
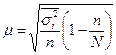
Серійний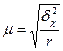
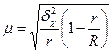
помилка вибірки для частки
Випадковий і механічний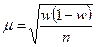
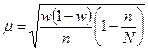
Типовий (районований)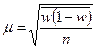
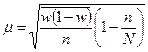
Серійний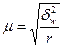

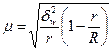
Особливість обчислення помилок репрезентативності для середньої величини при різних способах відбору полягає в тому, що для її обчислення в основу беруться різні показники дисперсій. При випадковому і механічному відборі для обчислення помилки вибірки використовується загальна дисперсія σ² для середньої і w (1 - w) — для частки.

Коли відбір одиниць здійснюється з окремих типово однорідних груп, виділених за відповідною ознакою, варіації групових середніх немає, і похибка типової вибірки залежить від середньої величини з групових 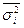для середньої і 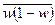- для частки.

В разі серійної вибірки, яка передбачає суцільне спостережен­ня одиниць у відібраних серіях, похибка вибірки залежить не від числа обстежених одиниць сукупності, від кількості відібраних серій. Похибка вибірки залежатиме не від варіації ознаки у всій сукупності, а від варіації серійних середніх, яка вимірюється міжгруповою дисперсією середньої σ²_х. При обчисленні середньої помилки вибірки для частки ознаки в основі розрахунку є міжгрупова (міжсерійна) дисперсія вибіркової частки 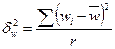. Похибка вибірки для частки ознаки при серійному відборі залежить від числа серій у генеральній сукупності — R і числа відібраних серій — r.

У формулах для обчислення помилок вибірки при безповторному відборі у підкореневий вираз формул повторного відбору додається множник 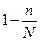або .

Безповторний відбір гарантує точніші результати, оскільки він виключає можливість обстеження одних і тих самих одиниць при відборі з генеральної сукупності.

У статистичному аналізі часто постає потреба порівняння похибки вибірки різних ознак або однієї і тієї ознаки в різних сукупностях. Такі порівняння виконують за допомогою відносної помилки, яка показує на скільки відсотків вибіркова оцінка може відхиля­тися від параметра генеральної сукупності. Відносна стандартна помилка середньої — це коефіцієнт варіації вибіркових середніх:

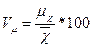
Для узагальнюючої характеристики помилки вибірки поряд із середньою розраховують і граничну помилку вибірки. Стверджувати, що дана генеральна середня не вийде за межі середньої помилки вибірки можна лише з певним ступенем імовірності.

У випадку вибіркового спостереження гранична помилка репрезентативності Δ може бути більшою, чи дорівнювати, або меншою від середньої помилки репрезентативності μ. Тому граничну помилку репрезентативності обчислюють з певною ймовірністю Р, якій відповідає t- разове значення μ. Відповідно до показника кратності помилки і формула граничної помилки репрезентативності має такий вигляд:

Δ=tμ; ,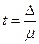

де Δ — гранична помилка вибірки, μ — середня помилки вибірки, t — коефіцієнт довіри, який залежить від ймовірності, з якою гарантується значення граничної помилки вибірки.

Формула граничної помилки вибірки випливає з основних положень теорії вибіркового методу, сформульованих у теоремах ймовірностей, що відображують закон великих чисел.

Однією із головних теорем, яку покладено в основу теорії вибіркового методу, є теорема П.Л. Чебишева, за допомогою якої він довів, що з ймовірністю, скільки завгодно близькою до одиниці, можна стверджувати, що при достатньо великому числі незалежних спостережень вибіркова середня буде мало відрізнятися від генеральної середньої при проведенні повторної вибірки.

Академік А.А. Марков довів збереження цієї умови для залежних спостережень (без повторної вибірки). Академік А.М. Ляпунов дослідив, що ймовірність відхилень вибіркової середньої від генеральної середньої при достатньо великому обсязі вибірки та обмеженій дисперсії генеральної сукупності підпорядковується закону нормального розподілу. Ймовірність цих відхилень при різних значеннях і визначається за формулою:

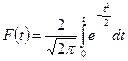
Значення цього інтеграла при різних значеннях t табульовані і наводяться в спеціальних таблицях, наприклад:

t = 1 Р(Δ ≤ μ) = 0,683

t = 2 Р(Δ ≤ μ) = 0,954

t = 3 Р(Δ ≤ μ) = 0,997

t = 4 Р(Δ ≤ μ) = 0,999

Ці показники означають, що з ймовірністю 0,683 можна стверджувати, що гранична помилка вибірки не перевищує μ, тобто в 68,3% випадків помилка репрезентативності не виходить за межі ±μ. Інакше, в 683 випадках із 1000 помилка репрезентативності не перевищує одного значення середньої помилки. З ймовірністю 0,954 можна стверджувати, що помилка репрезентативності не перевищує ±2μ, з ймовірністю 0,997 — не перевищить ±3μ. З ймовірністю 0,999, тобто дуже близькою до одиниці, можна очікувати, що різниця між вибірковою і генеральною середніми не перевищить чотириразової помилки вибірки.

Гранична помилка вибірки розраховується за вибірковим спостереженням по-різному, залежно від видів і способів відбору. Вона дає можливість встановити, в яких межах лежать значення генеральної середньої або частки. В таблиці 7.3 наведені формули для обчислення граничної помилки вибірки в різних умовах її здійснення:

Таблиця 7.3. Граничні помилки вибірки

Спосіб відбору	Метод відбору
повторний	безповторний
помилка вибрки для середньої величини
Випадковий і механічний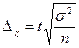
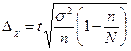
Типовий (районований)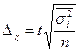
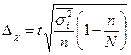
Серійний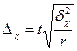
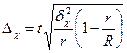
помилка вибірки для частки
Випадковий і механічний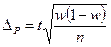
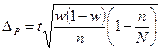
Типовий (районований)
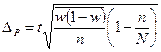
Серійний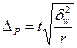

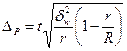
За допомогою формул граничної похибки вибірки визначають:

1. довірчі межі генеральної середньої і частки з певною ймовірністю;

2. ймовірність того, що відхилення між вибірковими і генеральними характеристиками не перевищує визначену величину;

3. необхідну чисельність вибірки, яка із заданою ймовірністю забезпечує очікувану точність вибіркових показників.

Розглянемо розв'язання цих завдань на прикладах:

Приклад 1. Припустимо, що при 2% випадковому відборі у відібраних для обстеження 100 деталей встановлено, що середня вага однієї деталі 2500г, дисперсія 900, зі 100 деталей 10 виявилися бракованими. З ймовірністю 0,954 встановити межі середньої ваги однієї деталі в генеральній сукупності, а з ймовірністю 0,997 — межі частки якісних деталей у генеральній сукупності.

Граничну похибку Δх=tμ, визначаємо за формулою безповторного відбору. Чисельність генеральної сукупності 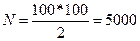шт..

За спеціальною таблицею знаходимо, що для ймовірності 0,954 t = 2, а для ймовірності 0,997 t =3. Таким чином,

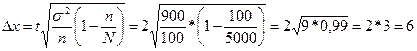г.

Звідси визначаємо довірчі межі генеральної середньої:

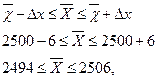
тобто з ймовірністю 0,954 можна стверджувати, що середня вага однієї деталі в генеральній сукупності лежить в межах від 2494 до 2506г.

Аналогічно визначаємо межі для генеральної частки. Вибіркова частка якісних деталей ω = 90: 100 = 0,9. Отже, гранична похибка частки

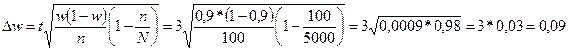
Генеральна частка W=w±Δw=w±tμ

Довірчі межі генеральної частки:

w-tμ≤W≤w+tμ

0,9-0,09≤ Р ≤0,9+0,09

0,81≤ Р ≤0,99

Отже, з ймовірністю 0.997 можна гарантувати, що частка якісних деталей у генеральній сукупності не виходить за межі від 81 до 99%.

Приклад 2. Посівна площа під кукурудзою в селянських, спілках регіону становить 5000га. Посіви розташовані на 50 стогектарних ділянках. Для визначення врожайності способом серійної безповторноі вибірки відібрано п'ять стогектарних ділянок, на яких здійснено суцільний облік зібраного врожаю кукурудзи (табл. 7.4):

Таблиця 7.4. Показники врожаю кукурудзи

Номер ділянки	Середній урожай на ділянці, ц/га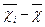
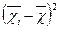
		-2
		-1
Разом			і0

Визначимо середню урожайність на всіх ділянках:

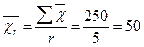ц/га

Між групова (міжсерійна) дисперсія

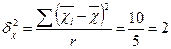
Тоді гранична помилка серійної вибірки при ймовірності Р=0,954:

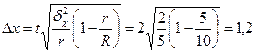ц/га

Звідси

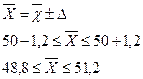
Отже, з ймовірністю 0,954 можна стверджувати, що середня врожайність кукурудзи в цілому регіоні коливається в межах від 48,8 до 5і,2 ц/га.

Під час вибіркового спостереження важливо правильно визначити необхідну чисельність обсягу вибірки, яка з відповідною ймовірністю забезпечує встановлену точність результатів спостереження. Надмірна чисельність вибірки призводить до затягнення строків дослідження, зайвих витрат часу і коштів, недостатня ж дає результати з великою похибкою репрезентативності.

Визначення необхідної чисельності вибірки залежить від алгебраїчного перетворення формул граничної похибки вибірки при різних способах відбору. Формули необхідної чисельності вибірки при повторному і безповторному відборах наведені в таблиці 7.4:

Таблиця 7.4. Чисельність вибірки

Спосіб відбору	Визначення середньої	Визначення частки
Повторний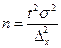
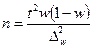
Безповторний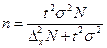

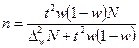
Аналіз наведених в таблиці 7.4 формул дає підстави стверджувати, що чисельність вибірки залежить:

1. від розміру граничної помилки. Чим точніші результати треба одержати, тобто з меншою помилкою вибірки, тим більшою повинна бути чисельність вибірки;

2. від показників варіації ознаки та частки. Чим більші варіації, тим більше треба взяти одиниць для вибіркового спостереження;

3. від ймовірності, з якою вимагається гарантувати результати вибірки. Чим більша ймовірність, тим більший коефіцієнт кратності, тим більшою повинна бути чисельність вибірки.

Покажемо застосування цих формул на прикладі:

Припустимо, що для господарства, в якому є 8000 корів, необхідно організувати: вибіркове обстеження з метою встановлення середньої річної молочної продуктивності корів. Якою має бути чисельність вибірки?

Якщо орієнтуватися на повторний відбір, то в разі граничної похибки 30кг, ймовірності Р=0,954 і середнього квадратичного відхилення 300кг, визначеного за результатами аналогічних обстежень, необхідна чисельність вибірки становитиме:

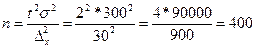корів

При без повторному відборі за тих самих умов необхідна чисельність вибірки становитиме:

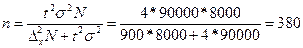корів

Цей розрахунок підтверджує, що за тих самих умов обсяг вибірки при безповторному відборі завжди менший, ніж при повторному.

Частку породних корів з похибкою до 5% за ймовірності 0,954 і дисперсії альтернативної ознаки 0,25 знаходимо необхідну чисельність вибірки:

- при повторному відборі:

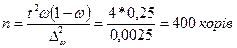
- при без повторному відборі:

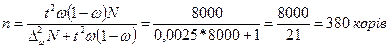
Отже, забезпечити очікувану точність при повторному відборі можна, досліджуючи 400 корів, а при без повторному відборі — 380.

В практичних розрахунках чисельності вибірки стикаються з труднощами, що і при розрахунку середньої помилки: відсутні показники мінливості одиниць сукупності σ та w(і-w).

Проблему вирішують таким чином: замість фактичних значень σ² та ω підставляють їх наближені значення, встановлені або на підставі попереднього обстеження, або на підставі пробних вибіркових обстежень.

Для частки ознаки в сукупності питання про дисперсію вирішується простіше. Справа в тому, що дисперсія альтернативної ознаки змінюється так: при w(1-w) будемо мати:

w = 0,2 0,2 (1-0,2) = 0,і6

w = 0,3 0,3 (1 - 0,3) - 0,2і

w = 0,4 0,4 (1 - 0,4) = 0,24

w = 0,5 0,5 (1-0,5) = 0,25

w = 0,6 0,6 (1-0,6) = 0,24

w = 0,7 0,7 (1-0,7) = 0,2і

w = 0,8 0,8 (1-0,8) = 0,і6

Це означає, що максимальне значення дисперсії альтернативної ознаки може бути 0,25. Для визначення необхідної чисельності вибірки в процесі дослідження частки в розрахунках приймають максимальне значення дисперсії альтернативної ознаки 0,25.

Необхідну чисельність вибірки в разі серійного відбору визначають як відбір певної кількості серій, які забезпечують з відповідною ймовірністю потрібну точність результатів дослідження. Для повторного відбору необхідна чисельність вибірки

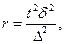а для безповторного - .

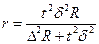У статистичній практиці вибіркове спостереження з великих масивів генеральної сукупності часто здійснюють у вигляді комбінованої, ступінчастої або кілька фазної вибірки. Вибіркова сукупність у разі комбіноваї вибірки формується внаслідок ступінчастого відбору.

Загалъна помилка для комбінованої вибірки складається з помилок, які можливі на кожному ступені, i визначається як корінь квадратний з квадратів помилок відповідних вибірок. Наприклад, якщо серійну вибірку скомбінувати з власне випадковою або механічною, то гранична помилка вибірки буде визначатись:

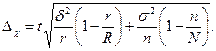
У разі моментного методу спостереження гранична помилка частки визначаеться як для звичайної повторної простої випадкової вибірки.

Наприклад, дослідник провів і20 спостережень i отримав шість відміток про те, що устаткування простоювало. Вибіркова питома вага буде становити 6:120 або 5%. Похибка вибірки з довірчою ймовіртстю Р = 0,954:

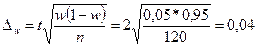
w-Δ≤W≤w+Δ

0,05-0,04≤W≤0,05+0,04

0,01≤W≤0,09

Висновок: з ймовірністю 0,954 можна стверджувати, що частка простоїв устаткування за весь робочий час лежить у межах від 1 до 9 %.

Відбір моментів здійснюють за схемою механічної вибірки або за схемою випадкової вибірки за таблицею випадкових чисел. Другий спосіб доцільно застосовувати в тих випадках, коли спостереження має бути для об'єкта несподіваним, аби не порушувати його звичайний трудовий ритм.

Визначають чисельність моментних спостережень за формулою граничної помилки випадкової повторної вибірки. Відбір у моментних спостереженнях завжди безповторний, однак формулу безповторного відбору застосовувати не можна, оскільки чисельність генеральної сукупностї моментів роботи визначити неможливо, вона нескінчена, якщо момент спостереження досить короткий. А тому необхідна чисельність мометів спостереження 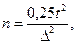якщо прийняти довірчу ймовірність Р=0,954, тобто коефіцієнт довіри t = 2, тоді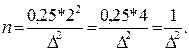

Наприклад, припустимо, що треба визначити число моментних спостережень за часом роботи устаткування, щоб гранична помилка не перевищувала 1 %, при ймовірності 0,954:

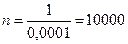спостережень

Якщо спостереження здійснюють протягом 25 днів i фіксують стан устаткування в моменти спостереження в 50 одиниць, тоді за день має бути 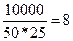спостережень за кожною одиницею.

Кінцевою метою будъ-якого вибіркового спостереження є поширення його характеристик на генеральну сукупність. На практиці застосовують різні способи поширення вибіркових даних.

Спосіб прямого перерахунку використовують у тому випадку, коли метою вибіркового обстеження є визначення обсягу ознаки в генеральній сукупності.

Наприклад, за результатами вибіркового спостереження середня урожайність круп'яних культур становить 25 ц/га, гранична помилка середньої при ймовірності 0,954-0,5 ц/га. У тому разі, коли загальна посівна площа під круп'яними культурами в генеральній сукупності становить 2000га, то можливий обсяг валового збору зерна з цієї площі буде не менше 49 тис. ц — 2000 (25 - 0,5), а максимальний валовий збір становитиме 51 тис. ц — 2000 (25 + 0,5).

Якщо вибіркове спостереження проводять з метою уточнения результатів суцільного спостереження, застосовують спосіб поправочних коефіцієнтів.

Наприклад, після проведения перепису худоби, що належить насе­ленню, провели 10%-й вибірковий контроль, під час якого визначили відсоток недообліку худоби. Згідно з даними перепису в господарствах, які попали у вибірку, поголів'я худоби становить 200 голів, а за даними вибірки 205. Отже, недооблік худоби становитиме (5: 200) 100 = 2,5%. Це той коефіцієнт, який слід розповсюдити на всю генеральну сукупність. Дані перепису худоби N = 10 000 відповідно коригуються: 10 000*1,025=10250 голів.

Дата добавления: 2013-12-14