Непараметрические показатели корреляции

Теоретическое корреляционное отношение

(индекс корреляции):

,

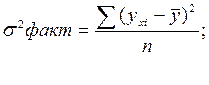
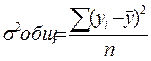
Значимость определяется по F – критерию Фишера:

, где

n - число наблюдений;

m – число параметров в уравнении регрессии.

Расчётное значение F – критерия сравнивается с критическим (табличным) для принятого уровня значимости и чисел степеней свободы k₁=m-1 и k₂=m-n.

Если F_расчёт>F_табл., то величина корреляционного отношения или индекса корреляции признаётся значимой, а связь между признаками существенной.

Формулы для расчёта факторной дисперсии:

Для линейной регрессии (уравнения прямой линии у_x=a + bх):

_;

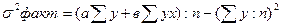для двучленной гиперболической регрессии (уравнения гиперболы у_х=):

для параболической регрессии (уравнение параболы 2-го порядка у=а+вх+сх²):

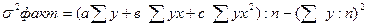
Коэффициент корреляции рангов (Спирмена ):

r =, где (4)

d – разность между рангами соответствующих величин двух признаков;

n – число единиц в ряду (число пар рангов).

Коэффициент корреляции рангов принимает любые значения от -1 до +1. Если все ранги строго изменяются в одном и том же порядке, то d=0, а r=1. Если же ранги изменяются строго в противоположных направлениях, то r= -1. Значение r=0 характеризует отсутствие связи.

Значимость коэффициента корреляции рангов для совокупностей небольшого объёма (n£30) проверяется по таблице предельных значений коэффициента корреляции рангов Спирмена при заданном уровне значимости a и определённом объёме совокупности.

Значимость r может быть проверена также на основе t – критерия Стьюдента. Расчётное значение критерия определяется по формуле:

t_расч⁼ r×

Значение коэффициента корреляции считается статистически существенным, если t_расч>t_табл при заданном уровне значимости a и числе степеней свободы k=n-2.

Ранговый коэффициент корреляции Кендалла рассчитывается по формуле:

t=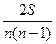, S=P+Q (5)

n – число наблюдений;

S – сумма разностей между числом последовательностей и числом инверсий по результативному признаку.

Расчёт данного коэффициента выполняется в следующей последовательности:

1) ранги факторного признака располагаются в порядке возрастания;

2) ранги результативного признака располагаются в порядке, соответствующем рангам признака х;

3) для каждого ранга результативного признака определяется сколько чисел, находящихся справа от него (следующих за ним) имеют величину ранга, превышающую его величину. Суммируя полученные таким образом числа, получаем слагаемое P, которое можно рассматривать как меру соответствия последовательностей рангов по x и y, и которое учитывается со знаком «+»;

4) для каждого ранга y определяется число, следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком «-»;

5) определяется сумма баллов S=P+Q

Коэффициент Кендалла также изменяется в пределах от -1 до +1.

Существенность коэффициента корреляции рангов Кендалла проверяется при выбранном уровне значимости a при больших n по формуле:

t>t_a×, где

t_a – коэффициент, определяемый по таблице нормального распределения.

При достаточно большом числе наблюдений между коэффициентами корреляции рангов Спирмена и Кендалла существует следующее соотношение: r».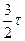

Связь между признаками можно считать существенной, если коэффициенты Спирмена и Кендалла больше ∣0,5∣.

Пример: определим степень тесноты связи между суммой затрат на рекламу сельскохозяйственной продукции и размером прибыли от ее продаж по данным десяти сельскохозяйственных предприятий района.

Таблица 6 – Исходные данные для корреляционного анализа

Номер предприятия	Затраты на рекламу сельскохозяйственной продукции, млн. руб.	Прибыль от продажи сельскохозяйственной продукции, млн. руб.
	3,6 4,6 17,2 2,6 7,0 7,6 9,0 11,6 7,4 13,0

Для проверки количественной однородности совокупности данных предприятий рассчитаем коэффициент вариации по факторному признаку.

Из расчетов видно, что V_x>33%, что свидетельствует о неоднородности совокупности, а, следовательно, о невозможности применения собственно-корреляционных методов изучения связи между признаками и, соответственно, о необходимости использования непараметрических методов.

Рассчитаем коэффициент корреляции рангов (коэффициент Спирмена) по формуле:

r =,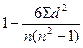

где d² – квадрат разности рангов, n – число наблюдений.

Для определения рангов каждого предприятия по факторному и результативному признаку проведем ранжирование, т.е. расположим предприятия в порядке возрастания значений признаков.

Таблица 7 – Ранжированные ряды распределения предприятий по затратам на рекламу и прибыли от ее продажи

Номер предприятия	Сумма затрат на рекламу продукции, млн. руб. x	Ранг предприятия Rx	Номер предприятия	Прибыль от реализации продукции, млн. руб. y	Ранг предприятия Ry
	2,6 3,6 4,6 7,0 7,4 7,6 9,0 11,6 13,0 17,2

Наиболее высокие ранги присваиваются предприятиям с наибольшими затратами на рекламу и наибольшим размером прибыли.

В таблице 8 произведем сравнение рангов каждого предприятия по факторному и результативному признаку.

Таблица 8 – Расчет данных для вычисления коэффициента Спирмена

Номер предприятия	Сравнение рангов	Разность рангов d=Rx-Ry	Квадрат разности рангов d^2
Rx	Ry
			-3 -1 -4 -1
Сумма	-	-	-

Подставим полученные данные в формулу коэффициента Спирмена:

r=

Таким образом, значение коэффициента корреляции рангов показывает умеренную по тесноте связь между затратами на рекламу сельскохозяйственной продукции и прибылью от ее продажи.

Определим степень тесноты связи между затратами на рекламу и размером прибыли от ее продажи с помощью коэффициента корреляции рангов Кендалла.

Для этого ряд рангов факторного признака упорядочим, приводя его к ряду натуральных чисел. Затем ранги результативного признака расположим в порядке, соответствующему рангам факторного признака. Для этого воспользуемся данными таблицы 7.

Так, первый ранг в ряду факторного признака имеет предприятие №4, для которого ранг по результативному признаку равен 4; второй ранг в ряду факторного признака имеет предприятие №1, для которого ранг по результативному признаку равен 1 и т.д.

Оформим данное упорядочение в виде таблицы.

Таблица 9 – Упорядоченные ряды рангов по факторному и результативному признаку

Ранг по факторному признаку
Ранг по результативному признаку

Для каждого ранга результативного признака определим, сколько следующих за ним значений рангов превышают его величину. Так, например, первому значению в последовательности рангов результативного признака, т.е. числу 4, соответствует 6 чисел (5,9,6,7,8,10), которые превышают ранг 4; второму значению 1 соответствует 8 чисел (3,5,9,6,7,8,10,2), третьему значению 3 соответствует 6 чисел (5,9,6,7,8,10) и т.д.

Суммируя полученные таким образом числа, получаем слагаемое P, которое рассматривают как меру соответствия последовательности рангов результативного признака последовательности рангов факторного признака. Для нашего примера

P=6+8+6+5+1+3+2+1+0=32.

Далее для каждого ранга результативного признака определим число следующих за ним рангов, меньших его величины. Эти величины берем со знаком минус. Так, первому значению в последовательности рангов результативного признака 4 соответствует 3 числа (1,3,2), которые меньше его; второе значение 1 не имеет рангов, меньших его и т.д.

Суммируя эти числа, получаем слагаемое Q, которое характеризует меру несоответствия последовательности рангов результативного признака последовательности рангов факторного признака.

Q=-3-0-1-1-4-1-1-1-1=-13

Суммируя величину P и Q, получаем величину S (S=P+Q=32-13=19), которая используется в формуле коэффициента Кендалла:

.

Дата добавления: 2013-12-14