Показатель эксцесса

Показатель асимметрии

ПОКАЗАТЕЛИ ФОРМЫ РАСПРЕДЕЛЕНИЯ

,

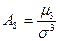где 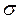–среднее квадратическое отклонение;

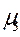– центральный момент третьего порядка

.

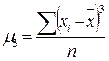Средняя квадратическая ошибка коэффициента асимметрии:

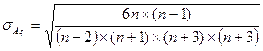, где

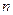- число наблюдений.

Если 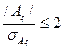- асимметрия несущественна (ее наличие объясняется наличием случайных обстоятельств) и распределение признака в генеральной совокупности можно считать нормальным.

Показатель асимметрии по формуле Линдберга:

,

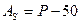где Р– процент тех значений признака, которые превосходят по величине среднюю арифметическую данного ряда;

50– удельный вес вариант, превосходящих среднюю арифметическую ряда нормального распределения.

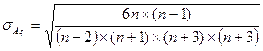
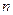- число наблюдений

;

.

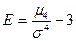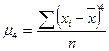Средняя квадратическая ошибка коэффициента эксцесса:

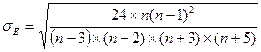
Если 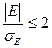– эксцесс несущественен и распределение можно отнести к разряду нормального.

Показатель эксцесса по формуле Линдберга:

,

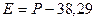где Р–удельный вес вариант, лежащих в интервале, равном половине среднего квадратического отклонения в ту и другую сторону от величины средней данного ряда;

38,29– удельный вес вариант, лежащих в интервале, равном половине среднего квадратического отклонения в ту и другую сторону от величины средней ряда нормального распределения.

ПРОВЕРКА СООТВЕТСТВИЯ ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОМУ РАСПРЕДЕЛЕНИЮ

Критерий согласия Пирсона (хи-квадрат) вычисляется по формуле:

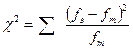, где

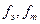–соответственно эмпирические и теоретические частоты.

Рассчитанное значение критерия сравнивается с табличным значением 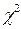при соответствующем числе степеней свободы и заданном уровне значимости (0,05 или 0,01).

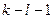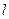Число степеней свободы равно , где –число групп, –число общих характеристик теоретического распределения (для нормального распределения 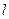=2).

Если 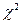расч..> 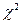табл., – расхождение между эмпирическими и теоретическими частотами существенно; гипотеза о близости эмпирического распределения к теоретическому отвергается.

Если 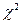расч..≤ 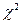табл., – рассчитанный критерий не превышает максимально возможную величину расхождений эмпирических и теоретических, которая может возникнуть в силу случайных причин; гипотеза о близости эмпирического распределения к теоретическому не отвергается.

Критерий Романовского:

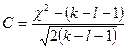, где

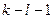–число степеней свободы (для нормального распределения: ).

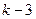При С< 3 различие частот несущественно, что позволяет считать эмпирическое распределение близким к теоретическому.

Критерий Ястремского:

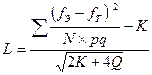, где

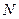–объём совокупности;

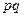–дисперсия альтернативного признака;

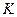–число вариантов или групп;

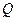–принимает значение 0,6 при числе вариантов или групп от 8 до 20.

Если 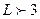, то эмпирическое распределение соответствует теоретическому.

Критерий Колмогорова:

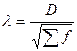, где

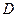–максимальное значение разности между накопленными эмпирическими и теоретическими частотами;

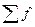–сумма эмпирических частот.

Дата добавления: 2013-12-14