
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сила давления на плоскую горизонтальную и наклонную поверхности. Гидростатический парадокс
|
|
|
|
Имеем сосуд (рис.8,а) с глубиной воды h. Давление жидкости в какой-либо точке сосуда зависит от глубины погружения этой точки. Если взять точки A, В и C, то давления в них будут соответственно равны
р А = ρ∙g∙h A; р B = ρ∙g∙h B; р C = ρ∙g∙h C.
Сила гидростатического давления на горизонтальную площадку S C
F C = ρ∙g∙h C ∙S C.
Сила гидростатического давления на все дно сосуда площадью S может быть определена по формуле
F = ρ∙g∙h∙S.
|
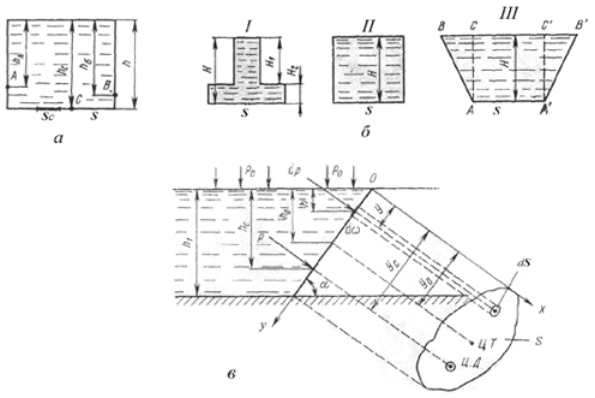
Следовательно, суммарная сила давления жидкости на горизонтальную поверхность равна весу столба жидкости, расположенной над рассматриваемой поверхностью.
На рис. 8,б изображены три сосуда различной формы. Площадь дна S всех трех сосудов одинакова. Все сосуды наполнены однородной жидкостью на глубину H. На рис. 8,б H = H1 + H2 Гидростатическое давление на дно во всех сосудах будет одинаковым и равным р = ρ∙g∙Н.
Суммарная сила гидростатического давления на дно любого из трех показанных на рис. 8,б сосудов будет также одинаковой и равной F=р∙S=ρ∙g∙H∙S. Спрашивается, откуда в сосуде I берется дополнительная сила по сравнению c сосудом II и куда пропадает избыток веса жидкости в сосуде III по сравнению c сосудом II? Нет ли здесь противоречия с законами физики?
Законы гидравлики утверждают, что давление жидкости не зависит от формы сосуда, а зависит от глубины погружения площади и ее размеров. В этом и заключается гидростатический парадокс, который может быть объяснен особым свойством жидкости передавать внешнее давление одинаковой величины по всем направлениям (закон Паскаля). Например, на дно сосуда III действует суммарная сила гидростатического давления F=ρ∙g∙H∙S. Что касается жидкости, находящейся в объемах (АВС) В 1 и (А'В'С') В', то ее вес воспринимается наклонными стенками, a не дном сосуда. Безусловно, если сосуд III будет стоять на столе, то стол воспринимает вес всей жидкости, находящейся в сосуде. Следовательно, никакого противоречия между законами физики и гидравлики не существует. Суммарная сила гидростатического давления на дно сосуда зависит от плотности жидкости, глубины наполнения сосуда и величины площади его дна и не зависит от формы сосуда.
B практике часто встречаются плоские поверхности (щиты, стенки), расположенные под каким-либо углом α к горизонту.
Выведем расчетную зависимость для определении силы давления жидкости на наклонную плоскую стенку (рис. 8,в), для чего выделим элементарную площадку dS, расположенную на глубине h. Центр тяжести щита (Ц.T) погружен на глубину h 0, площадь стенки равна S. Выберем оси координат так, как это показано на рисунке. Ось х совпадает с линией пересечения плоскости стенки и свободной поверхности, a ось у направлена вдoль стенки. Справа изображена стенка в плоскости хоу. Эту проекцию мы получим, если плоскость стенки повернем относительно оси у на 90°. На площадку dS будет действовать элементарная сила гидростатического давления
dF = dS (ρgh + р 0 )
где ρ - плотность жидкости, кг/м3; ρgh - избыточное гидростатическое давление, Па; р 0 - давление на свободной поверхности, Па.
Суммарная сила давления F жидкости на весь щит равна сумме элементарных сил, действующих по всей смоченной площади щита. Проинтегрировав по площади S будем иметь
 .
.
B свою очередь
h = y∙sin α,
тогда
 ,
,
где  - статический момент площади относительно оси x.
- статический момент площади относительно оси x.
Как известно, статический момент площади равен произведению площади на расстояние у 0 от центра его тяжести до рассматриваемой оси. Следовательно,
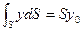 .
.
На рис. 8,в видно, что у 0 ∙sinα = h 0. Тогда, подставляя значение статического момента и заменяя через h 0 получим
F = S (ρgh 0 + p 0 ). (13)
При p 0 = p a на щит будет действовать слева атмосферное давление и справа давление со стороны жидкости, направленные навстречу друг к другу. Поэтому формула для этого случая будет иметь вид
F = ρgh 0 S.
Видно, что суммарная сила давления жидкости на плоскую поверхность равна произведению площади смоченной фигуры на давление в центре ее тяжести. Нетрудно видеть также, что сила F состоит из двух слагаемых: внешней силы суммарного гидростатического давления р 0 S и силы избыточного давления ρgh 0 S. Первая сила приложена в центре тяжести фигуры. Точка приложения второй силы (центр давления) располагается ниже центра тяжести.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 4930; Нарушение авторских прав?; Мы поможем в написании вашей работы!