Потери на трение при ламинарном течении в трубах

ГИДРАВЛИЧЕСКИЕ ПОТЕРИ.

Кавитационное течение.

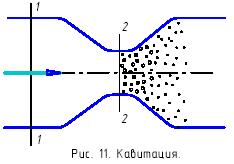Рассмотрим течение жидкости через трубку изображенную на рис.11. B месте сужения потока (сечение 2-2) скорость жидкости увеличивается, а давление уменьшается и, если его величина станет равным давлению насыщенных паров, то начинается интенсивное парообразование (кипение). Двигаясь вместе с жидкостью пузырьки газов, попадают в расширяющуюся часть трубки, где скорость уменьшается, а давление возрастает. Выделившиеся газы и пары конденсируются и пузырьки "схлопываются".

Такое явление получило название кавитации, а течение - кавитационное. Кавитация сопровождается характерным шумом и вибрацией, а при длительном воздействии - постепенным разрушением (эрозией) металлических стенок. Кавитация может иметь место в гидромашинах, а также на лопастях гребных винтов.

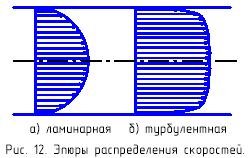При лaминарном течении эпюра распределения скоростей 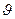по сечению потока носит параболический характер (рис.12,а) и описывается уравнением

, (21)

где - потери давления на трение в трубе длиной l;

µ - динамическая вязкость жидкости;

r и r ₀- текущий радиус и радиус трубы.

Такой закон распределения скоростей определяет величину коэффициента Кариолиса для ламинарного режима течения = 2 (см. раздел 3.4). Кроме того, зависимость (21) позволяет найти соотношение максимальной 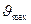(на оси потока) и средней 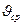скоростей: 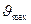/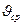= 2.

Кроме того, формула (21) позволяет получить закон сопротивлении при ламинaрном режиме течения (закон Пуазейля) в круглой трубе, т.е. зависимость потерь от расхода Q

(22) или , (23)

где и 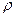- кинематическая вязкость и плотность рабочей жидкости;

- потери напора на трение в трубе.

Анализ зависимостей (22) и (23) позволяет сделать вывод, что при ламинарном режиме течения потери на трение пропорциональны расходу жидкости (рис.13).

Формула для вычисления коэффициента Дарси для ламинарного режима может быть получена из совместного решения уравнений (22) и (19), первое из которых справедливо только для ламинарного течения, а второе - при любом течении. Тогда, с учетом (20),

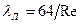. (24)

Таким образом, величина коэффициента Дарси при ламинарном режиме течения однозначно определяется числом Рейнольдса.

Дата добавления: 2013-12-14