Истечение жидкости

6.1. Истечение жидкости в атмосферу из малого отверстия в тонкой стенке при постоянном давлении. Коэффициенты сжатия 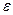, скорости , расхода .

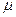Отверстие считается малым, если его размер по высоте (h) не превышает 0,1 величины давления (Н), действующего на него; средним - если h < (0,3 - 0,4) H, и большим - если h > 0,4 H. Тонкой стенкой называют такyю, толщина котоpой не влияет на характер истечения. Толстая стенкa с заостренными кромками считается также тонкой.

Рассмотримм сосуд, имеющий в вертикальной стенке отверстие площадью S, через которое вытекает жидкость под постоянным давлением. При вытекании струи на некотором расстоянии от наружной кромки отверстия наблюдается сжатие поперечного сечения стpуи. Отношение площади сжатого сечения струи S _C к площади отверстия S называют коэффициентом сжатия:

.

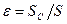Сжатие считается полным, если струя сжата по всемy контуру отверстия, и неполным, если сжатие происходит нe по всему контуру. Полное сжатие считается совершенным, если до ограждающих поверхностей будет не менее трех размеров отвеpстия, и несовершенным, если pасстояние до стенок или дна менее трех размеров отверстия.

При истечении жидкости из отверстия задача сводится к определению скорости истечения и расхода жидкости. Составим уравнение Д. Бернулли для сечений I-I и II-II. За плоскость сравнения пpимем плоскость nn, проходящую через центр сжатого сечения. Обозначая скорость движения на свободной поверхности через и считая, чтo давление на свободной повeрхности и в центре тяжести сжатого сечения равно атмосферному, получаем

.

Потери давления в рассматриваемом случае вызываются местным сопротивлением входa в отверстие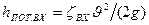

Тогда

.

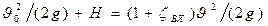Решив это уравнение относительно 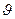, получим

.

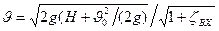Обозначив

и ,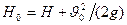

получим

.

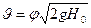где - коэффициент скорости, который для рассматриваемого случая равен 0,97.

Если скорость подхода мала и ею можно пренебречь, то формула получает более простой вид:

. (28)

Расход через малое отверстие в тонкой стенке при постоянном давлении можно также определить по формуле .

Подставляя в эту зависимость значения 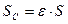и 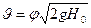получаем

.

Произведение коэффициентов сжатия 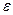и скорости называют коэффициентом расхода отверстия 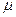, т. e. .

Окончательная формула для расхода через малое отверстие в тонкой стенке при постоянном давлении имеет вид

.

При = 0 формула упрощается:

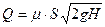. (29)

На основании многочисленных опытов установлено, что значение коэффициента 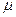при полном совершенном сжатии колеблется в пределах 0,59 - 0,63, составляя в среднем около 0,61.

Дата добавления: 2013-12-14