Дискретная СВ. Закон распределения вероятностей

Понятие случайных величин (СВ)

Случайные величины и их распределения

Ограниченность введенных в лекции 1 понятий случайных событий, вероятности и действий над ними лишь простейшими схемами отображения реальных ситуаций очевидна. Поэтому аппарат “Событий” в современной ТВ не является основным. Он лишь создает необходимую теоретическую базу для перехода к более обобщенному, более основному понятию ТВ – понятию СВ, способам их описания и манипулирования с ними, которое боле адекватно отображает реальные процессы массовых случайных явлений и их проявляемые закономерности.

В чем заключена ограниченность:

1) событие, как результат опыта может появляться или не появляться, то есть характеристика качественная(!), в то время, как результаты реальных событий чаще всего могут характеризоваться совокупностью значений, выраженных числом из некоторой последовательности, интервала, совокупности…

2) Вероятность рассматривается лишь для случаев, т.е. равновозможных событий из состава полной группы. А это не всегда так!

3) Простейшая ‘Уровневая схема’ вычисления вер., далека от реальности.

Исторически понятием СВ начали пользоваться еще в 18 веке, но никто не пытался дать ему определения. Лишь к середине 19 в. этот термин появился, причем не был строго определен. На интуитивном уровне он просуществовал во всех учебниках до 20-х годов 20 в. И лишь в 30-х годах сформировалось четкое теоретико-множественное определение данное Колмогоровым. Мы дадим нестрогое определение случайным величинам, а затем конкретизируем их для СВ прерывного и непрерывного типа.

Случайной величиной называют такую величину, которая в результате опыта может принять то или иное значение, причем какое именно – заранее указать нельзя.

СВ могут быть одномерными и многомерными:

Одномерная СВ (скалярная) – результатом опыта является одно число

Многомерная СВ (векторная) – результатом опыта является целый набор значений различных характеристик

СВ также подразделяются на дискретные и непрерывные:

Дискретная СВ (СВ прерывного, дискретного типа) – такая СВ, которая в результате опыта может принимать счетное (конечное или бесконечное) количество различных значений (заранее можно указать все значения или их пронумеровать).

Непрерывная СВ (СВ непрерывного типа) – такая СВ, которая в результате опыта может принимать любое значение из данного интервала (таких значений бесконечное множество)

Давайте сделаем еще один шаг к более строгому пониманию СВ.

Определение: Величина Х называется дискретной СВ, если множество ее возможных (различных) значений представляет собой конечную или бесконечную последовательность чисел x₁, x₂,…, x_i,… и если каждое событие Х = x_i является случайным событием, т.е. имеет определенную вероятность P_i. (события Х = x_i будем называть элементарными событиями).

Т.е. для задания дискретной СВ необходимо задать все возможные элементарные события (значения) и их вероятности (они могут быть различны!) – или иными словами определить закон распределения.

Законом распределения СВ Х называют любое правило, позволяющее находить соответствие между возможными значениями x_i и их вероятностями.

Р(Х=x_i) = P_i, для любого i =1, 2, …

Закон распределения можно задать таблично, аналитически (в виде формулы), графически.

А) Табличный способ задания ЗР СВ

i
xi
Pi

Б) Графический способ

В) Аналитический способ

Примеры типовых распределений дискретных величин:

1) Биномиальный закон распределения

Биномиальным называют закон распределения дискретной СВ X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p (а не появления соответственно q).

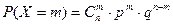
m – число раз появления события

2) Закон распределения Пуассона

Если число испытаний велико, а вероятность p появления события в каждом испытании очень мала, то используют приближенную формулу:

,

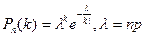и говорят, что случайная величина распределена по закону Пуассона

Дата добавления: 2013-12-14