Лекция 1. Патологическая анатомия

ШШшя

Управление нервной системой работы сердца

Особенности функций миокарда

Сердечный цикл

Фазы сердечного цикла

1. Автоматизм-способность сердца самопроизвольно возбуждаться и сокращаться без внешних раздражителей.

2. Наличие в сердечном цикле фаз изометрического сокращения и изометрического расслабления.

3. Закон сердца Старлинга- сила сокращения сердца зависит от его кровенаполнения.

4. Неспособность к тетаническому сокращению, что связано с длительным возбуждением и рефрактерностью, что делает невозможным суммацию одиночных мышечных сокращений.

5. Подчинение закону «Все или ничего», что объясняется проведением возбуждения с одного кардиомиоцита на соседние через электрические контакты-нексусы.

6. Возможность возникновения внеочередных сокращений сердца- экстрасистол.

Изобарное

охлаждение

W

0 V-

Рис. 4.2. Изобарный процесс идеального газа

3). Изотермический процесс (Рис.4.3).

Т = Const, Т2 = Т1 Уравнение состояния:

P1 / P2 = v 2 / v 1, (4.16) Так как Т₂ = Т₁, то Au = 0 и уравнение 1-го закона т/д будет иметь вид:

q = l = R-T-ln(v 2/v 1), (4.17) или q = l = R-T-ln(P1/P2), (4.18) где R = R_n/ n - газовая постоянная [Дж/(кг-К)].

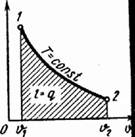Рис. 4.3. Изотерм и ский процесс идеала ного газа

4). Адиабатный процесс (Рис.4.4).

В данном процессе не подводится и не отводится тепло, т.е. q =0. Уравнение состояния:

P- v ^X = Const, (4.19) где X = c_p / c_v - показатель адиабаты. Уравнение 1-го закона т/д будет иметь вид:

l = -Ли = = -ev-(t2 - ti) = ev-(ti - t2), (4.20)

или

l = R-(Ti - T2) / (X -1); (4.21) l = R-T1-[1 - (v 1/ v 2) ^{X -1}] /(X - 1); (4.22) 1 = RT₂-[1 - (P₂/P0^(X"^1)/X] /(к- 1). (4.23)

П

О a-

Рис.4.4. Взаимное расположение адиабаты и изо­термы идеально­го газа в р-, о-диаграмме

4.3. Политропный процесс.

Политропным процессом называется процесс, все состояния которого удовлетворяются условию:

P- vⁿ = Const, (4.24) где n - показатель политропы, постоянная для данного процесса. Изобарный, изохорный, изотермический и адиабатный процессы являются частными случаями политропного процесса (Рис.4.5): при n = ± да v = Const, (изохорный), n = 0 P = Const, (изобарный), n = 1 T = Const, (изотермический), n = X P- v = Const, (адиабатный).

Работа политропного процесса определяется аналогично как при адиабатном процессе:

1 = R-(T1 - T2) / (n - 1); (4.25) 1 = R-Tr[1 - (v 1/ v 2) ^n-1] /(n - 1); (4.26) 1 = R-Tr[1 - (P2/P1) ^{(n-1)/ n}] /(n - 1). (4.27)

Теплота процесса:

q = Cn -(T2 - T1), (4.28) где c_n = c_v -(n - A,)/(n - 1) - массовая теплоемкость (4.29) политропного процесса.

Рис. 4,5. Политропные процессы идеального газа; 1 — изобара, 2— изотер­ма, 3— адиабата, 4 — изо- хорз

Тема 5. Термодинамика потока.

5.1. Первый закон термодинамики для потока.

На практике при рассмотрении рабочих процессов машин, аппаратов и устройств, встречаются задачи изучении закономерностей движения рабочих тел (газов, пара и жидкостей).

Уравнение 1-го закона термодинамики для потока газа при следующих допущениях:

• движение газа по каналу установившееся и неразрывное;

• скорости по сечению, перпендикулярному оси канала, постоянны;

• пренебрегается трение частичек газа друг другу и о стенки канала;

• изменение параметров по сечению канала мало по сравнению их абсолютными значениями,

имеет вид:

q = Ли + Ле + 1прот. + 1техн., (5.1)

где Ле = (w^[1]₂ - w²₁)/2 + g-(z₂ -z₁) - изменение энергии системы, состоящий из изменения кинетической и потенциальной энергий; w1,w2 - скорости потока в начале и в конце канала; z1, z2 - высота положения начала и конца канала.

q = (U2 - ui) + (w²2 - w²i)/2 + g-(Z2 -zi) + P2-V 2 - PfV i + 1техн. (5.2) Введем понятия энтальпии, который обозначим через величину: h = u + Px, (5.3)

h2 = U2 + P2-V 2; hi = Ui + Pi-V i. (5.4) Тогда уравнение i-го закона термодинамики для потока газа будет иметь вид: q = h2 - hi + (w²2 - w²i)/2 + g-(z2 -zi) + 1техн. (5.5)

5.2. Критическое давление и скорость. Сопло Лаваля.

Если перемещение газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называется соплом. Если в канале происходит сжатие рабочего тела с увеличением его давления и уменьшением скорости, то такой канал называют диффузором.

В каналах при небольшой разности давлений газа и внешней среды скорость течения рабочего тела достаточно большая. В большинстве случаев длина канала небольшая и процесс теплообмена между стенкой и газом незначителен, поэтому процесс истечения газа можно считать адиабатным.

Скорость истечения (на выходе канала) определяется из уравнения: w = w₂ = v 2(h_i - h₂). (5.6)

или

w = v 2V/(y - i)-Pi-x i [i - (P2/Pi)^(y"^i)/y]. (5.7) Массовый секундный расход газа, [кг/с]:

m = f-w/x 2, (5.8) где: f - площадь сечения канала на выходе. Так как процесс истечения адиабатный, то:

m = f-V 2у/(у - i)-Pi/x i-[(P2/Pi)^2/y - (P2/Pi)^(y+i)/y]. (5.9)

Массовый секундный расход идеального газа зависит от площади выходного канала, начального состояния газа и степени его расширения.

Критическим давлением называется такое давление на выходном сечении канала, при котором достигается максимальный расход газа и определяется следующим выражением:

Pk = P2 = Рк-Pi, (5.i0)

где: Pk = (2/(у + 1))^г/(г-1). для одноатомных газов: у =1,66 9 р_к = 0,49; для двухатомных газов: у =1,4 9 р_к = 0,528; для трехатомных газов: у =1,3 9 р_к = 0,546.

Критической скоростью называется скорость газа в выходном сечении канала, при давлении равном или меньшем критического - P_k.

wk = V 2(у/(у + i))-Pi-x 1. (5.11)

Критическая скорость зависит при истечении идеального газа только от начальных параметров, его природы и равна скорости звука газа (а) при критических параметрах.

wk = а = V у-Pk'Xk. (5.12)

Комбинированное сопло Лаваля предназначено для использования больших перепадов давления и для порлучения скоростей истечения, превышающих критическую или
скорость звука. Сопло Лаваля состоит из короткого суживающегося участка и расширяющейсяя конической насадки (Рис.5.1). Опыты показывают, что угол конусности расширяющейся части должен быть равен а = 8-12^о. При больших углах наблюдается отрыв струи от стенок канала.

Р 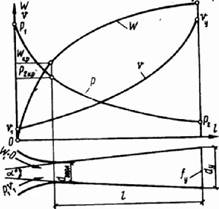Рис, 5.1. графики измененияр, w,vпри истечении через комбинирован­ное сопло

Скорость истечения и секундный расход идеального газа определяются по формулам (5.7)

l = (D - d) / 2-tgfa/2), (5.13)

где: ф - угол конусности сопла;

D - диаметр выходного отверстия;

d - диаметр сопла в минимальном сечении.

5.3.Дросселирование.

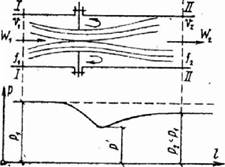Рис. 5,2,К вопросу о дросселирова­нии газов

Любой кран, вентиль, задвижка, клапан и прочие местные сопротивления, уменьшающие

Дросселированием называется явление, при котором пар или газ переходит с высого давления на низкое без совершения внешней работы и без подвода или отвода теплоты. Такое явление происходит в трубопроводе, где имеется место сужения проходного канала (Рис.5.2). При таком сужении, вследствие сопротивлений, давление за местом сужения - Р₂, всегда меньше давления перед ним - Р₁.

проходное сечение трубопровода, вызывают дросселирования газа или пара, следовательно падения давления. В большинстве случаев это явление приносит безусловный вред. Но иногда оно является необходим и создается искусственно (регулирование паровых двигателей, в холодильных установках, в приборах для измерения расхода газа и т. д.).

При прохождении газа через отверстие, кинетическая энергия газа и его скорость в узком сечении возрастают, что сопровождается падением температуры и давления. Газ, протекая через отверстие, приходит в вихревое движение. Часть его кинетической энергии затрачивается на образование этих вихрей и превращается в теплоту. Кроме того, в теплоту превращается и работа, затраченная на преодоление сопротивлений (трение). Вся эта теплота воспринимается газом, в результате чего температура его изменяется (уменьшается или увеличивается).

В отверстие скорость газа увеличивается. За отверстием газ опять течет по полному сечению и скорость его вновь понижается. А давление увеличивается, но до начального значения оно не поднимается; некоторое изменение скорости произойдет в связи с увеличением удельного объема газа от уменьшения давления.

Дросселирование является необратимым процессом, при которм происходит увеличение энтропии и уменьшение работоспособности рабочего тела. Уравнением процесса дросселирования является следующее уравнение:

i1 = 12. (5.14)

Это равенство показывает, что энтальпия в результате дросселирования не изменяется и справедливо только для сечений, достаточно удаленных от сужения. Для идеальных газов энтальпия газа является однозначной функцией температуры. Отсюда следует, что при дросселировании идеального газа его температура не изменяется (Т1 = Т2).

При дросселировании реальных газов энтальпия газа остается постоянной, энтропия и объем увеличиваются, давление падает, а температура изменяется (увеличивается, уменьшается или остется неизменной).

Изменение температуры жидкостей и реальных газов при дросселировании называется эффектом Джоуля-Томсона. Для идеального газа эффект Джоуля-Томсона равен нулю. Различают дифференциальный температурный эффект, когда давление и температура изменяются на бесконечно малую величину, и интегральный температурный эффект, при котором давление и температура изменяются на конечную величину. Дифференциальный температурный эффект обозначается - б:

а = (ST/oP)i. (5.15)

Интегральный температурный эффект определяется из следующего уравнения: ЛT = T2 - T1 = J [T-(5v/5T)p - v] / Cp dP. (5.16)

Для реальных газов Л^0 и может иметь положительный или отрицательный знак. Состояние газа, при котором температурный эффект меняет свой знак, называется точкой инверсии, а температура, соответствующая этой точке, называется температурой инверсии - Т_инв.

Тинв = v-(dT/9d v)p. (5.17)

Тема 6. Реальные газы. Водяной пар. Влажный воздух.

6.1. Свойства реальных газов.

Реальные газы отличаются от идеальных газов тем, что молекулы этих газов имеют объемы и связаны между собой силами взаимодействия, которые уменьшаются с увеличением расстояния между молекулами. При практических расчетах различных свойств реальных газов наряду с уравнением состояния применяется отношение P-v/(R-T)=c, которая называется коэффициентом сжимаемости.

Так как для идеальных газов при любых условиях P-v = R'T, то для этих газов с = 1. Тогда величина коэффициента сжимаемости выражает отклонение свойств реального газа от свойств идеального. Величина с для реальных газов в зависимости от давления и температуры может принимать значения больше или меньше единицы и только при малых давлениях и высоких температурах она практически равна единице. Тогда реальные газы можно рассматривать как идеальные.

В связи с отличием свойств реального газа от свойств идеального газа нужно иметь новые уравнения состояния, которые связывали бы значения P, x, T и давали бы возможность рассчитывать некоторые свойства газов для разных условий. Были предложены многочисленное число различных уравнений состояния реальных газов, но ни одно из них не решает проблему для общего случая. Развитие кинетической теории газов, позволило установит точное уравнение состояния реальных газов в виде:

P-v = R-[1 - Zv /(v + 1)-Bv / v^V]. (6.1)

B_V - вириальные коэффициенты, выражаются через потенциальные энергию взаимодействия молекул данного газа и температуру Т.

Однако это уравнение в общем виде не может быть использовано для непосредственных расчетов реальных газов. Для отдельных частных случаях получены расчетные уравнения того или иного реального газа. Из-за сложности вычисления вириальных коэффициентов обычно ограничиваются расчетом первых двух коэффициентов. Тогда расчетное уравнение имеет вид:

P-v = R-(1 - А/v - B / V²), (6.2)

где А и В - первый и второй вириальные коэффициенты, являющиеся функцией только температуры.

При расчете свойств многих реальных газов уравнения такого типа получили большое распространение.

6.2. Уравнения состояния реального газа.

Наиболее простым и качественно верно отображающим поведение реального газа, является уравнение Ван-дер-Ваальса:

(P + a/v²)-(v - b) = RT. (6.3)

а, b - постоянные величины, первая учитывает силы взаимодействия, вторая учитывает размер молекул.

a/v² - характеризует добавочное давление, под которым находится реальный газ вследствие сил сцепления между молекулами и называется внутренним давлением. Для жидких тел это давление имеет большие значения (например, для воды при 20⁰С составляет 1050 Мпа), а для газов из-за малых сил сцепления молекул оно очень мало. Поэтому внешнее давление, под которым находится жидкость, оказывает ничтожное влияние на её объем, и жидкость считают несжимаемой. В газах в виду малости значения a/v внешнее давление легко изменяет их объем.

Уравнение Ван-дер-Ваальса качественно верно отображает поведение жидких и газообразных веществ, для двухфазных состояний оно неприменимо. На PV - диаграмме (рис.6.1) показаны изотермы построенные по уравнению Ван-дер- Ваальса. Из кривых видно, что при сравнительно низких температурах имеются волнообразные участки. Чем выше температура, тем короче эти части кривых. Эти волнообразные кривые указывают на непрерывный переход от жидкого состояния в парообразное при данной температуре. Точка А соответствует состоянии жидкости, точка В относится парообразному состоянии вещества.

В действительности переход из жидкого состояния в парообразное всегда происходит через двухфазное состояние вещества. При этом при данной температуре процесс перехода происходит также и при постоянном давлении. Этот действительный переход из жидкого состояния в парообразное изображается прямой линией АВ.

Практически для особо чистых веществ возможно осуществление участков волнообразной кривой AQ и DB. В первом случае имеют место неустойчивые состояния перегретой жидкости, а во втором - переохлажденного пара.

При определенной температуре изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка (точка К). Эту температуру называют критической. Если соединить точки А₁, А₂, А₃... и В₁, В₂, В₃... получим кривую похожую на параболу. Кривая АК называется нижней пограничной кривой и соответствует в состоянии кипения жидкости. Кривая КВ называется верхней пограничной кривой и соответствует состояния сухого насыщенного пара.

Таким образом, для реального вещества PV - диаграмму можно разбить на 3 области:

1 - область жидкого состояния, расположена левее нижней пограничной кривой;

2 - область двухфазных состояний (влажный пар), расположена между нижней и верхней пограничной кривой);

3 - область перегретого пара, расположена правее верхней пограничной кривой и выше критической точки. Условно область жидкости ограничивают сверху линией КМ - критическая изобара.

Критическую температуру Д.И.Менделеев называл абсолютной температурой кипения, при которой поверхностное натяжение в жидкости становится равным нулю, т.е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщенным паром). Связь между критическими параметрами и постоянными уравнения Ван-дер-Ваальса:

Тк = 8-а/(27-^Ь); Рк = a/(27-b²); (6.4) а = (27- R² -Т²к)/(64 -Рк); Ь = (27- R -Тк)/(8 -Рк). (6.5)

Уравнение Ван-дер-Ваальса при больших плотностях газа дает значительные ошибки. Кроме этого экспериментальным путем доказана, что коэффициенты а, b зависят от температуры и давления, причем эта зависимость очень сложная. М.П.Вукалович и И.И.Новиков в 1939 г. предложили новое универсальное уравнение состояния реальных газов с учетом ассоциации и диссоциации их молекул, который имеет следующий вид:

(Р + a/v²)-(v - b) = R-T (1 - С/(v -т^(3+2ш)/2), (6.6) где a, b - постоянные уравнения Ван-дер-Ваальса; С, m - постоянные, определяемые на основании опытных данных.

6.3. Понятия о водяном паре.

Одним из распространенным рабочим телом в паровых турбинах, паровых машинах, в атомных установках, теплоносителем в различных теплообменниках является водяной пар.

Пар - газообразное тело в состоянии, близкое к кипящей жидкости.

Парообразование - процесс превращения вещества из жидкого состояния в парообразное. Испарение - парообразование, происходящее всегда при любой температуре с поверхности жидкости.

При некоторой определенной температуре, зависящей от природы жидкости и давления, под которым она находится, начинается парообразование во всей массе жидкости. Этот процесс называется кипением.

Обратный процесс парообразования называется конденсацией. Она также протекает при постоянной температуре.

Процесс перехода твердого вещества непосредственно в пар называется сублимацией. Обратный процесс перехода пара в твердое состояние называется десублимацией. При испарении жидкости в ограниченном пространстве (в паровых котлах) одновременно происходит обратное явление - конденсация пара. Если скорость конденсации станет равной скорости испарения, то наступает динамическое равновесие. Пар в этом случае имеет максимальную плотность и называется насыщенным паром.

Если температура пара выше температуры насыщенного пара того же давления, то такой пар называется перегретым. Разность между температурой перегретого пара и температурой насыщенного пара того же давления называется степенью перегрева. Так как удельный объем перегретого пара больше удельного объема насыщенного пара, то плотность перегретого пара меньше плотности насыщенного пара. Поэтому перегретый пар является ненасыщенным паром.

В момент испарения последней капли жидкости в ограниченном пространстве без изменения температуры и давления образуется сухой насыщенный пар. Состояние такого пара определяется одним параметром - давлением.

Механическая смесь сухого и мельчайших капелек жидкости называется влажным паром. Массовая доля сухого пара во влажном паре называется степенью сухости - х.

х = Шсп / Швп, (6.7) т_сп - масса сухого пара во влажном; ш_вп - масса влажного пара.

Массовая доля жидкости во влажном паре нызвается степенью влажности - у. у = 1 - v. (6.8)

Для кипящей жидкости при температуре насыщения v= 0, для сухого пара - v= 1.

6.4. Характеристики влажного воздуха.

Атмосферный воздух, в основном состоящий из кислорода, азота, углекислого газа,

содержит всегда некоторое количество водяного пара.

Смесь сухого воздуха и водяного пара называется влажным воздухом.

Влажный воздух при данном давлении и температуре может содержать разное количество

водяного пара. Если смесь состоит из сухого воздуха и насыщенного водяного пара, то его

называют насыщенным влажным воздухом. В этом случае во влажном воздухе находится

максимально возможное для данной температуры количество водяного пара. При

охлаждении этого воздуха, будет происходить конденсация водяного пара. Парциальное

давление водяного пара в этой смеси равно давлению насыщения при данной

температуре.

Если влажный воздух содержит при данной температуре водяной пар в перегретом состоянии, то он будет называться ненасыщенным. Так как в нем находится не максимально возможное для данной температуры количество водяного пара, то он способен к дальнейшему увлажнению. Поэтому такой воздух используют в качестве сушильного агента в различных сушильных установках.

По закону Дальтона общее давление влажного воздуха равно сумме парциальных давлений сухого воздуха и водяного пара, входящих в его состав:

Р = рв + рп, (6.9)

где: Р_В - парциальное давление сухого воздуха; РП - парциальное давление водяного пара.

Максимальное значение Р_П при данной температуре влажного воздуха t представляет собой давление насыщенного водяного пара - Р_н.

Для нахождения парциального давления пара пользуются специальным прибором - гигрометром. С помощью этого прибора определяют точку_росы, т.е. температуру (t_p), до которой нужно охладить при постоянном давлении воздух, чтобы он стал насыщенным. Зная точку росы, можно по таблицам определить парциальное давление пара в воздухе как давление насыщения (Р_н), соответствующее точки росы t_p.

Абсолютной влажностью воздуха называется количество водяных паров, находящихся в 1 м³ влажного воздуха. Абсолютная влажность равна плотности пара при его парциальном давлении и температуре воздуха - ^.

Отношение абсолютной влажности ненасыщенного воздуха при данной температуре к абсолютной влажности насыщенного воздуха при той же температуре называется относительной влажностью воздуха

Ф = с_п / с_н или ф = с_п / с_н -100%, (6.10)

Для сухого воздуха ф = 0, для ненасыщенного ф < 1, для насыщенного ф = 1(100%). Если водяной пар считать как идеальный газ, то по закону Бойля-Мариотта отношение плотностей можно заменить отношением давлений. Тогда:

Ф = РП / Рн или р = рп / Рн -100%. (6.11)

Плотность влажного воздуха слагается из масс, содержащихся в 1 м³ сухого воздуха и водяных паров:

Р = Рв + Рп = Pb/(Rb'T) + ф/v'. (6.12) Молекулярная масса влажного воздуха определяют по формуле: || = 28,95 - 10,934ф Pн/P (6.13)

Значения Р_Н и v при температуре воздуха t берутся из таблицы водяного пара, ф - по данным психрометра, P - по барометру.

Влагосодержание - представляет собой отношение массы пара к массе сухого воздуха:

d = Мп / Мв, (6.14)

где: М_П, М_В - соответственно массы пара и сухого воздуха во влажном воздухе. Связь между влагосодержанием с относительной влажностью:

d = 0,622 ф-Рн-/(Р - Ф-Рн). (6.15) Газовая постоянная:

R = 8314/м = 8314/(28,95 - 10,934-|д-Рн/Р). (6.16) Объем влажного воздуха, приходящегося на 1 кг сухого воздуха:

Увл.в = R-T/P. (6.17) Удельный обьем влажного воздуха:

v = Увл.в/(1 + d). (6.17) Удельная массовая теплоемкость паровоздушной смеси:

ссм = св + d-сп. (6.18)

Тема 7. Термодинамические циклы. 7.1. Циклы паротурбинных установок (ПТУ).

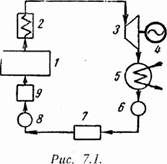
Паротурбинная установка является основой современных тепловых и атомных электростанций. Рабочим телом в таких установках является пар какой-либо жидкости (водяной пар). Основным циклом в паротурбинной установке является цикл Ренкина. Принципиальная схема ПТУ показана на рис.7.1 и процесс получения работы происходит в следующим образом. В паровом котле (1) и в перегревателе (2) теплота горения топлива передается воде. Полученный пар поступает в турбину (3), где происходит преобразование теплоты в механическую работу, а затем в электрическую энергию в электрогенераторе (4). Отработанный пар поступает в конденсатор (5), где отдает теплоту охлаждающей воде. Полученный конденсат насосом (6) отправляется в питательный бак (7), откуда питательным насосом (8) сжимается до давления, равного в котле, и подается через подогреватель (10) в паровой котел (1).

Рассмотрим цикл Ренкина на насыщенном паре. Схема установки отличается от предыдущей схемы тем, что в данном случае будет отсутствовать перегреватель. Поэтому на турбину будет поступать насыщенный пар. На рис.7.2,а изображен цикл Ренкина в TS- диаграмме. Процессы:

3-1 - подвод теплоты от источника в воде q₁, состоит из двух процессов: 3-3^/ - кипение воды в котле;

3-1 - испарение воды в пар при постоянном давлении;

1- 2 - в турбине пар расширяется адиабатически;

2- 2^/ - пар конденсируется и отдает тепло q2 охлаждающей воде; 2^/-3 - конденсат адиабатически сжимается.

Термический к.п.д. цикла Ренкина определяется по уравнению:

nt = ⁽q1 ^- q2^)/q1. ⁽⁷.¹⁾

Так как: q1 = h1 - h3; q2 = h2 - h2^/,

то

nt = [(h1 - h2) - (h3 - h2)] /(h1 - h3) = 1 / q1. (7.2) Полезная работа цикла равна разности работ турбины и насоса:

тн

/

1н = h3 - h2

где: 1т = h1 - h2

В основном 1_т >> 1_н, тогда считая h₃ = h₂, можно записать:

nt = (h1 - h2)/(h1 - h3). (7.3) Теоретическуя мощность турбины рассчитывают по формуле:

Nt = (h1 - h2)-D/3600, [Вт] (7.4) где: D = 3600-m - часовой расход, [кг/ч] m - секундный расход, [кг/с]

а)

Цикл Ренкина на перегретом паре применяется для увеличения термического к.п.д. цикла ПТУ. Для этого перед турбиной ставят перегреватель 2 (Рис.7.1), котрый увеличивает температуру и давление пара. При этом возрастает средняя температура подвода теплоты в цикле. Диаграмма цикла показана на рис.7.2,б Формулы расчета 1, n_t, Nt остаются без изменений.

тцТТн^

5)

Рис. 7.2. Цикл Ренкина на насыщенном {а} и лерегретом (б) паре

7.2. Циклы двигателей внутреннего сгорания (ДВС).

Циклы поршневых двигателей внутреннего сгорания подразделяют на три группы:

• с подводом теплоты при постоянном объеме (карбюраторные ДВС);

• с подводом теплоты при постоянном давлении (компрессорные дизели);

• со смещанным подводом теплоты при постоянном объеме (безкомпрессорные дизели);

Основными характеристиками или параметрами любого цикла теплового двигателя являются следующие безрамерные величины:

степень сжатия (отношение удельных объемов рабочего тела в начале и конце сжатия) 8 = V1 / V2, (7.5)

степень повышения давления (отношение давлений в конце и в начале изохорного процесса подвода теплоты)

к = Рз / Р2, (7.6)

степень предварительного расширения или степень изобарного расширения (отношение удельных объемов в конце и в начале изохорного процесса подвода теплоты) Р = V3 / V2. (7.7)

1). Рассмотрим цикл ДВС с подводом теплоты при постоянном объеме на примере четырехтактного двигателя.

Диаграмма реального двигателя представлена на рис.7.3.

С	fcs	F<
i f
	! 7,
ш		' т—1 ■ I! i
т	-i
	! /

Рис. 7.3. Цикл двигателя внутреннего сгорания с подводом теплоты при постоянном объеме

а-1 (1 такт) - в цилиндр через всасывающий клапан поступает смесь воздуха и паров горючего (нетермодинамичемкий процесс);

1- 2 (2 такт) - адиабатное сжатие (повышается температура);

2- 3 - сгорание горючей смеси, давление быстро возрастает при постоянном объеме (подвод теплоты q₁);

3- 4 (3 такт) - адиабатное расширение (рабочий процесс, совершается полезная работа);

4- а - открывается выхлопной клапан и отработанные газы покидают цилиндр давление цилиндра падает (отводится тепло q2).

1-а (4 такт) - выталкивание оставшихся в цилиндре газов. Затем процесс повторяется.

Описанный процесс является необратимым (наличие трения, химической реакции в рабочем теле, конечные скорости поршня, теплообмен при конечной разности температур и т. п.).

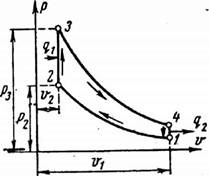
Для анализа теории тепловых машин термодинамика рассматривает идеальные циклы обратимые циклы. Диаграмма идеального процесса двигателя внутреннего сгорания показана на рис.7.4.

Рис. 7.4.

Из этой диаграммы выводится формула для термического к.п.д. цикла с подводом теплоты при постоянном объеме, который имеет следующий вид:

nt = 1 - 1/s^y, (7.8)

где: s -степень сжатия (основной показатель работы двигателя, чем выше е, тем выше экономичность ДВС); Y - показатель адиабаты.

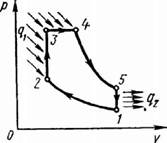
2). Идеальный цикл ДВС со смешанным подводом теплоты при постоянном объеме (безкомпрессорные дизели). Диаграмма цикла показана на рис.7.5.

Рис, 7.5. Цикл двигате­ля внутреннего сгора­ния со смешанным под­водом теплоты

1- 2 - чистый воздух с температурой Т₁ сжимается до температуры Т₂, которая больше температуры воспламенения топлива. В этот момент в цилиндр через форсунки под давлением впрыскивается топливо.

2- 3 - горючая смесь самовоспламеняется и к рабочему телу подводится тепло q₁^/, давление повышается до Р₃.

3- 4 - поршень перемешается обратно, поступление и сгорание топлива продолжается при постоянном давлении и подводится тепло q₁^//.

4- 5 - поршень продолжает перемещаться в нижнюю мертвую точку, давление падает (адиабатное расширение);

5- 1 - процесс отвода теплоты q2 при постоянном объеме (через выпускной клапан покидают отработанные газы).

Термический к.п. д. цикла определяется по формуле:

nt = X - (X-p^y - 1) / s^y-1-[(X - 1) + уХ-(р - 1)]. (7.9) Цикл двигателей с подводом теплоты при постоянном давлении широкое применение не нашли, так как у этих циклов очень большой коэффициент сжатия.

7.3. Циклы газотурбинных установок (ГТУ).

Основными недостатками поршневых двигателей внутреннего сгорания явяляются ограниченность их мощности и невозможность адиабатного расширения рабочего тела до атмосферного давления, котрые отсутствуют в газотурбиннных установках. ГТУ рабочим телом являются продукты сгорания жидкого или газообразного топлива. На рис.7.6 дана схема простейшей газотурбинной установки со сгоранием топлива при постоянном давлении. Топливным насосом 5 и компрессором 4 топливо и воздух через форсунки 6 и 7 поступают в камеру сгорания 1. Из камеры продукты сгорания направляются в комбинированные сопла 2, где они расширяются, и поступают на лопатки газовой турбины 3.

Рис/З.б.

На рис.7.7 и рис7.8 представлены идеальный цикл ГТУ на PV и TS диаграммах.

Рис. 7.8.

1- 2 - адиабатное сжатие до давления Р₂;

2- 3 - подвод теплоты q₁ при постоянном давлении Р₂ (сгорание топлива);

3- 4 - адиабатное расширение до первоначального давления Р₁;

4- 1 - охлаждение рабочего тела при постоянном давлении Р₁ (отвод теплоты q₂); Характеристиками цикла являются:

степень повышения давления - X = Р₂/ Р₁; степень изобарного расширения - р = v₃ /v₂. Работа турбины:

1т = h3 - h4. (7.10)

Работа компрессора:

1н = h2 - h1. (7.11) Полезная работа ГТУ равна разности работ турбины и компрессора:

Ьгту = 1т - 1к. (7.12) Термический к.п. д. цикла ГТУ имеет вид: nt = 1 - 1/ X ^(у-1)/у. (7.13) Теоретическая мощность газовой турбины, компрессора и установки (ГТУ): N = 1_т-Б/3600 = (h₃ - h₄)-D/3600, (7.14) N = IkD/3600 = (h2 - h1)-D/3600, (7.15) Кгту = 1гту" D/3600 = [(h₃ - h₄) (h₂ - h₁) ]-D/3600. (7.16)

Действительный цикл ГТУ отличается от теоретического наличием потерь на трение и вихреообразование в турбине и компрессоре. Эффективными методами повышения экономичности газотурбинных установок являются: регенерация теплоты, ступенчатое сжатие и расширение рабочего тела и пр.

Раздел II. Основы теории теплообмена.

Тема 8. Основные понятия и определения.

Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:

• теплопроводностью;

• конвекцией;

• излучением (радиацией).

Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами тел с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела, кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии. Конвекция - это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых жидкости или газа. При этом, перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностью. Одновременный перенос теплоты конвекцией и теплопроводностью называется конвективным теплообменом. В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей. Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется излучением (радиацией). Этот процесс происходит в три стадии: превращение части внутренней энергии одного из тел в энергию электромагнитных волн, распространение э/м волн в пространстве, поглощение энергии излучения другим телом. Совместный теплообмен излучением и теплопроводностью называют радиационно- кондуктивнымтеплообменом.

Совокупность всех трех видов теплообмена называется сложным теплообменом. Процессы теплообмена могут происходит в различных средах: чистых веществах и разных смесях, при изменении и без изменения агрегатного состояния рабочих сред и т. д. В зависимости от этого теплообмен протекает по разному и описывается различными уравнениями.

Процесс переноса теплоты может сопровождаться переносом вещества (массообмен). Например испарение воды в воздух, движение жидкостей или газов в трубопроводах и.т.п. и. т. д. Тогда процесс теплообмена усложняется, так как теплота дополнительно переносится с массой движущегося вещества.

Тема 9.Теплопроводность.

9.1. Температурное поле. Уравнение теплопроводности.

Будем рассматривать только однородные и изотропные тела, т.е. такие тела, которые обладают одинаковыми физическими свойствами по всем направлениям. При передачи теплоты в твердом теле, температура тела будет изменяться по всему объему тела и во времени. Совокупность значений температуры в данный момент времени для всех точек изучаемого пространства называется температурным полем:

t = f(x,y,z,T), (9.1) где:! -температура тела; x,y,z -координаты точки; т - время.

Такое температурное поле называется нестационарным dt/di ^ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности

Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:

t = f(x,y,z), at/di = 0 (9.2) Уравнение двухмерного температурного поля: для нестационарного режима:

t = f(x,y,T); dt/dz = 0 (9.3) для стационарного режима:

t = f(x,y), dt/dz = 0; dt/di = 0 (9.4) Уравнение одномерного температурного поля: для нестационарного режима:

t = f(x,T); at/5y = dt/dz = 0; dt/di * 0 (9.5) для стационарного режима:

t = f(x); dt/dy = dt/dz = 0; dt/di = 0 (9.6) Изотермической поверхностью называется поверхность тела с одинаковыми температурой.

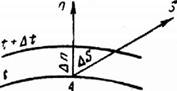
Рассмотрим две изотермические поверхности (Рис.9.1) с температурами t и t + Д{.Градиентом температуры называют предел отношения изменения температурь^к расстоянию между изотермами по нормали Дп, когда стремится к нулю: gradt = jgradtj = Нш[Д{/Дп]дп^0 = dt/dn (9.7)

Рис. 9.1.

Температурный градиент-это вектор, направленной по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной температуры t по нормалии:

gradt = dt/dn no, (9.7*) где:п₀ - единичный вектор.

Количество теплоты, проходящее через изотермическую поверхность F в единицу времени называется тепловым потоком - Q, [Вт=Дж/с].

Тепловой поток, проходящий через единицу площади называют плотностью теплового потока - q = Q / F, [Вт/м²]

Для твердого тела уравнение теплопроводности подчиняется закону Фурье: \\Тепловой поток, передаваемая теплопроводностью,\\пропорциональна градиенту температуры и площади сечения,\\перпендикулярного направлению теплового потока.

Q = -X-F- dt/dn, (9.8)

или

q = -X • dt/dn -no = -X-gradt, (9.9)

где: q - вектор плотности теплового потока; X - коэффициент теплопроводности, [Вт/(м-К)]. Численное значение вектора плотности теплового потока равна: q = -X- a/Sn = -X-|gradt|, (9.10)

где:|§га&|- модуль вектора градиента температуры.

Коэффициент теплопроводности является физическим параметром вещества, характеризующим способность тела проводит теплоту, Она зависит от рода вещества, давления и температуры. Также на её величину влияет влажность вещества. Для большинства веществ коэффициент теплопроводности определяются опытным путем и для технических расчетов берут из справочной литературы.

Дифференциальное уравнение теплопроводности для трехмерного нестационарного температурного поля имеет следующий вид:

,(9.11)

где: а = hf(p-p) -коэффициент температуропроводности [м /с], характеризует скорость изменения температуры.

Для стационарной задачи, дифференциальное уравнение имеет вид:

.(9.12)

9.2. Стационарная теплопроводность через плоскую стенку.

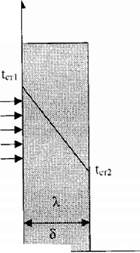
1). Однородная плоская стенка (Рис.9.2.). t QU^...:.........:.. Рис.9.2. Однородная плоская стенка.

Температуры поверхностей стенки -^_т1 и tcr₂. Плотность теплового потока:

q = -X- dt/dn = - X- a/dx = - X- (t_c-r₂ - ^_т1)/(х_ст2 - х_ст1)- или

q = X- (^т2 - Ът1)/(Хст2 - ХстО' At/Ax (9.13)

температурный напор; - толщина стенки.

Тогда

q = Х/5-0ст1 - Ы = Х/5-At, (9.14) Если R =5/Х -термическое сопротивление теплопроводности стенки [(м²-К)/Вт], то плотность теплового потока:

q = (W - 1c2)/R. (9.15) Общее количество теплоты, которое передается через поверхность F за время т определяется:

Q = q-F-т = (11ст1 - teri2)/R-F-T. (9.16) Температура тела в точке с координатой х находится по формуле:

tx = 1ст1 - (1ст1 - "1ст2)-х/ 5. (9.17) 2). Многослойная плоская стенка.

Рассмотрим 3-х слойную стенку (Рис.9.3). Температура наружных поверхностей стенок1_ст1 и t_CT2, коэффициенты теплопроводности слоев^ь Хз, Хз, толщина слоевбь 82, 5з. t

Рйс.9.3. Многослойная плоская стенка

Плотности тепловых потокок через каждый слой стенки: q = ^1/51-(1ст1 - W), (9.18) q = ^-(W - 1сл2), (9.19) q = ^3/53-(1сл2 - 1ст2), (9.20) Решая эти уравнения, относительно разности температур и складывая, получаем:

q = (t1 - t4)/(51/^1 + 52/Х2 + 53/Х3) = (1ст1 - t_CT4)/Ro, (9.21) где: R_o = (5₁/Х₁ + 5₂/Х₂ + 5₃/Х₃) - общее термическое сопротивление теплопроводности многослойной стенки.

Температура слоев определяется по следующим формулам: 1сл1 = 1ст1 - q-(51/^1). (9.22) 1сл2 = 1сл1 - q-52Aa). (9.23)

9.3. Стационарная теплопроводность через цилиндрическую стенку.

1). Однородная цилиндрическая стенка.

Рассмотрим однородный однослойный цилиндр длиной 1, внутренним диаметром ё₁и внешним диаметром d₂ (Рис.9.4).

Температуры поверхностей стенки -t_CTi и t_CT2.

Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = - X-2-n-r -l- St / dr (9.24)

или

Q = 2-n-X-l-At/ln(d2/di), (9.25) где: At = W - t_ст2 - температурный напор; X - коэффициент теплопроводности стенки.

Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут:

qi = Q/l =2-n-X-At /ln(d2/di), [Вт/м]. (9.26) Температура тела внутри стенки с координатойdx:

tx = W - (tori - Ы -ln(d_x/di) / ln(d2/di). (9.27) 2). Многослойная цилиндрическая стенка.

Рис.9.4 Однослойная цилиндрическая стенка.

(il 4----------------- ► dj

Допустим цилиндрическая стенка состоит из трех плотно прилегающих слоев (Рис.9.5).

Рис.9.5. Многослойная цилиндрическая стенка,

Температура внутренней поверхности стенки -t_CTi, температуранаружнойповерхности стенки —;_ст2, коэффициенты теплопроводности слоев X₂, X₃, диаметры слоев d_1s d₂, d₃,

d4.

Тепловые потоки для слоев будут: 1-й слой

Q = 2-я- Ы-Ост! - tслl)/ ln(d2/di), (9.28)

2- й слой

Q = 2-я-VHW - Ы/ ln(da/d2), (9.29)

3- й слой

Q = 2-Я-V1-(tc2 - td2)/ 1n(d4/d3), (9.30) Решая полученные уравнения, получаем для теплового потока через многослойную стенку:

Q = 2-я-1-(^т1 - ЪстО / [1n(d2/d1)/^1 + 1n(d3/d2)/^2 + 1n(d4/d3>/X₃]. (9.31) Для линейной плотности теплового потока имеем:

q1 = Q/1 = 2-я- (t1 - t2) / [1n(d2/d1)/^1 + 1n(d3/d2)/^2 + 1п^3)/Ы (9.32) Температуру между слоями находим из следующих уравнений: W = W - q1-1n(d2/d1) / 2-я-^1. (9.33) tсл2 = W - qx-1n(d3/d2) / 2-Я-Х2. (9.34)

9.4. Стационарная теплопроводность через шаровую стенку.

или

Пусть имеется полый шар (Рис.9.6) - внутренний диаметр d₁, внешний диаметрd₂, температура внутренней поверхности стенки -^_т1, температуранаружнойповерхности стенки -t_ст2, коэффициент теплопроводности стенки -X. Уравнение теплопроводности по закону Фурье в сферических координатах:

Q = - Ы-я-г- dt / dr (9.35)

Q =4-n-X-At/(1/r2 - 1/Г1) =2-n-X-At/(1/d1 - 1/d2) = = 2-n-X-d1-d2-At /(d2 - d1) = n-MrdrAt / 5 (9.36)

где: At = W - ^_т2 - температурный напор; 5 -толщина стенки.

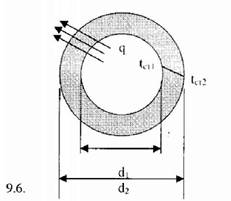Рис.9.6, Однородная шаровая стенка.

Тема 10. Конвективный теплообмен.

10.1. Факторы, влияющие на конвективный теплообмен.

Конвективным теплообменом называется одновременный перенос теплоты конвекцией и теплопроводностью.

В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей. Основными факторами, влияющими на процесс теплоотдачи являются следующие:

1). Природа возникновения движения жидкости вдоль поверхности стенки. Самопроизвольное движение жидкости (газа) в поле тяжести, обусловленное разностью плотностей её горячих и холодных слоев, называют свободным движением (естественная конвекция).

Движение, создаваемое вследствие разности давлений, которые создаются насосом, вентилятором и другими устройствами, называется вынужденным (вынужденная конвекция).

2). Режим движения жидкости.

Упорядоченное, слоистое, спокойное, без пульсаций движение называется ламинарным. Беспорядочное, хаотическое, вихревое движение называется турбулентным.

3). Физические свойства жидкостей и газов.

Большое влияние на конвективный теплообмен оказывают следующие физические параметры: коэффициент теплопроводности (X), удельная теплоемкость (с), плотность (р), ккоэффициент температуропроводности (а = Х/с_рф), коэффициент динамической вязкости (ц) или кинематической вязкости (v = ц/р), температурный коэффициент объемного расширения (в = 1/Т).

4). Форма (плоская, цилиндрическая), размеры и положение поверхности (горизонтальная, вертикальная).

10.2.Закон Ньютона-Рихмана.

Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона- Рихмана, которая гласит, что количество теплоты, передаваемая конвективным теплообменом прямо пропорционально разности температур поверхности тела (tv-r) и окружающей среды (Ъ_ж):

Q = a • (1'ст - t*>F, (10.1)

или

q = a • (t_CT - 1'ж), (10.2) где: коэффициент теплоотдачи [Вт/(м²К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

Факторы, которые влияют на процесс конвективного теплообмена, включают в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения:

a = f\(X; Ф; lo; xc; yc; zc; Wo; 0; Х; а; ср; р; v; в), (10.3) где: Х - характер движения среды (свободная, вынужденная); Ф - форма поверхности;

1_o - характерный размер поверхности (длина, высота, диаметр и т.д.);

xc; yc; zc - координаты;

Wo - скорость среды (жидкость, газ);

0 = (Ъст - Ъ_ж) - температурный напор;

Х - коэффициент теплопроводности среды;

а - коэффициент температуропроводности среды;

с_р -изобарная удельная теплоемкость среды; р -плотность среды;

v - коэффициент кинематической вязкости среды; в - температурный коэффициент объемного расширения среды.

Уравнение (10.3) показывает, что коэффициент теплоотдачи величина сложная и для её определения невозможно дать общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования. Достоинством экспериментального метода является: достоверность получаемых результатов; основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.

Основным недостатком этого метода является, что результаты данного эксперимента не могут быть использованы, применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.

10.3. Краткие сведения из теории подобия.

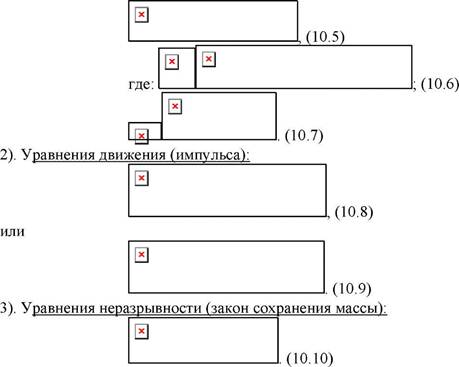
Для аналитического метода исследования конвективного теплообмена нужно решить систему дифференциальных уравнений, состоящий из: 1). Уравнения энергии (закон сохранения энергии):

(10.4) где: q„- внутренний источник тепла. или

4). Уравнение теплообмена (условие теплообмена на границе твердого тела и среды):

а = -X/At- dt / dr n=0. (10.11) Данные уравнения записаны для несжимаемой жидкости (? = Const).

Решение этих дифференциальных уравнений сложная и трудоемкая задача, и она возможна при ограниченных простых случаев. Поэтому при исследовании конвективного теплообмена применяют метод теории подобия.

Теория подобия - это наука о подобных явлениях. Подобными явлениями называются такие физические явления, которые одинаковы качественно по форме и по содержанию, т. е. имеют одну физическую природу, развиваются под действием одинаковых сил и описываются одинаковыми по форме дифференциальными уравнениями и краевыми условиями.

Обязательным условием подобия физических явлений должно быть геометрическое подобие систем, где эти явления протекают. Два физических явления будут подобны лишь в том случае, если будут подобны все величины, которые характеризуют их. Для всех подобных систем существуют безразмерные комплексы величин, которые называются критериями подобия.

Основные положения теории подобия формулируют в виде 3-х теорем подобия.

1 теорема: Подобные явления имеют одинаковые критерии подобия.

2 теорема: Любая зависимость между переменными, характеризую-щая какие-либо явления, может быть представлена, в форме зависимости между критериями подобия, составленными из этих переменных, которая будет называться критериальным уравнением.

3 теорема: Два явления подобны, если они имеют подобные условия однозначности и численно одинаковые определяющие критерии подобия.

Условиями однозначности являются:

• наличие геометрического подобия систем;

• наличие одинаковых дифференциальных уравнений;

• существование единственного решения уравнения пр заданных граничных условиях;

• известны численные значения коэффициентов и физических параметров.

10.4. Критериальные уравнения конвективного теплообмена.

Используя теорию подобия из системы дифференциальных уравнений 10.4, 10.9, 10.10 и 10.11 можно получить уравнение теплоотдачи (10.3) для конвективного теплообмена в случае отсутствия внутренних источников тепла в следующем критериальной форме:

Nu = f2(X; Ф; X0; Y0; Z0; Re; Gr; Pr), (10.12) где: X₀; Y₀; Z₀ - безразмерные координаты;

Nu = a -1₀/Х - критерий Нуссельта (безразмерный коэффициент теплоотдачи), характеризует теплообмен между поверхностью стенки и жидкостью (газом); Re = w1₀/v - критерий Рейнольдса, характеризует соотношение сил инерции и вязкости и определяет характер течения жидкости (газа);

Gr = (p-g-l₀³-At)/v² - критерий Грасгофа, характеризует подьемную силу, возникающую в жидкости (газе) вследствие разности плотностей;

Рг = v/а = (ц-с_р)/Х - критерий Прандтля, характеризует физические свойства жидкости (газа);

l₀ - определяющий размер (длина, высота, диаметр). 10.5. Расчетные формулы конвективного теплообмена.

Приведем некоторые основные расчетные формулы конвективного теплообмена (академика М. А.Михеева), которые даны для средних значений коэффициентов теплоотдачи по поверхности стенки.

1. Свободная конвекция в неограниченном пространстве.

а). Горизонтальная труба диаметром d при 10³<(Gr-Pr)_x^_d <10⁸.

Шжаср. = 0,5-(G^d -Рг ж)^0,25 (Рг ж/Ргст)^0,25. (10.13)

б). Вертикальная труба и пластина:

1). ламинарное течение - 10³<(Gr • Рг)_ж <10⁹:

Шжаср. = 0,75- (G^d •Рг ж)°^,25ЧРг ж/РГст)^0,25. (10.14) 2). турбулентное течение - (Gr - Рг)_ж > 10⁹:

Шжаср. = 0,15- (G^d -Рг ж)^0,33 -(Рг ж/Ргст)^0,25. (10.15) Здесь значения Gr^ и Рг _ж берутся при температуре жидкости (газа), а Рг_ст при температуре поверхности стенки.

Для воздуха Рг _ж/Рг_ст = 1 и формулы (10.13-10.15) упрощаются. 2. Вынужденная конвекция.

Режим течения определяется по величине Re.

а). Течение жидкости в гладких трубах круглого сечения.

1). ламинарное течение - Re < 2100

Шжаср. = 0,15^ежа^0,33-Ргж^0,33-^Гжа-Ргж)^0,1-(Ргж/Ргст)^0,25-81, (10.16) где s_l - коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы и зависит от отношения длины трубы к его диаметру (l/d). Значения этого коэффициента представлена в таблице 10.1. Таблица 10.1.

Значение s_l при ламинарном режиме.

l/d
Sl	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1,0

2). переходной _режим - 2100 < Re < 10⁴

Шж^р. = К0-Ргж^0,43-(Ргж/Ргст)^0,25-б1. (10.17) Коэффициент К₀ зависит от критерия Рейнольдса Re и представлена в таблице 10.2. Таблица 10.2. Значение К0.

Re?10^4

2,1

2,2

2,3

2,4

2,5

К0

i,9

2,2

3,3

3,8

4,4

6,0

i0,3

15,5

i9,5

27,0

33,3

3). турбулентное течение - Re = i0⁴

N^. = 0,02i- Reжd⁰'⁸•Pгж⁰'⁴³• (РГж/РГСТ)⁰'²⁵-В1. (i0.i8)

Таблица i0.3. Значение s_l при турбулентном режиме.

1/d
	Re = 2-i0^3	Re = 2^i0^4	Re = 240^5
i	i,9	i,51	1,28
	i,70	i,40	1,22
	i,44	i,27	1,15
i0	i,28	i, 18	1,10
i5	i, 18	i,i3	1,08
	i,i3	1,11	1,06
	i,05	1,05	1,03
	i,02	1,02	1,02
	i,00	1,00	1,00

б). Обтекание горизонтальной поверхности.

1). ламинарное течение - Re < Ф10 ⁴

Шж^р. = 0,66^d°'⁵-P^°'³³ •(Ргж/Ргст)^0,25. (i0.i9)

2). турбулентное течение - Re > Ф10 ⁴

Nuжdср. = 0,037^d⁰'⁵-P^⁰'³³ •(Ргж/Ргст)^0,25. (i0.20)

в). Поперечное обтекание одиночной трубы (угол атаки р = 90⁰).

1). при Re_Mdd = 5 - 10³

Шж^р. = 0,57^еж^0ЛРгж⁰'³⁸ •(Ргж/Ргст)^0,25. (10.21)

2). при Re_x^d = 10³ - 210⁵

Nuжdср. = 0,25 ^еж⁰'⁶Фгж⁰'³⁸ •(Ргж/Ргст)^0,25. (i0.22)

Тема 11. Тепловое излучение.

11.1. Общие сведения о тепловом излучении.

Лучистая энергия возникает за счет энергии других видов в результате сложных молекулярных и внутриатомных процессов. Природа всех лучей одинакова. Они представляют собой распространяющиеся в пространстве электромагнитные волны. Источником теплового излучения является внутренняя энергия нагретого тела. Количество лучистой энергии в основном зависит от физических свойств и температуры излучающего тела. Электромагнитные волны различаются между собой длиной волны В зависимости от длины волны X лучи обладают различными свойствами. Наименьшей длиной волны обладают космические лучи X = (0,1 - 10)^оА (где ^оА — ангстрем, единица длины, 1^оА = 10^-10м). Гамма-лучи, испускаемые радиоактивными веществами, имеют длину волны до 10^оА; лучи Рентгена - X = (10-200) ^оА; ультрафиолетовые лучи - л = (200^оА - 0,4 мк (мк — микрон, 1 мк — 0,001 мм), световые лучи - X = (0,4-0,8)мк, инфракрасные или тепловые лучи - X = (0,8 - 400) мк, радио или электромагнитные лучи - X > 400 мк. Из всех лучей наибольший интерес для теплопередачи представляют тепловые лучи с X = (0,8 - 40) мк.

Лучеиспускание свойственно всем телам, и каждое из них излучает и поглощает энергию непрерывно, если температура его не равна 0°К. При одинаковых или различных температурах между телами, расположенными как угодно в пространстве, существует непрерывный лучистый теплообмен.

При температурном равновесии тел количество отдаваемой лучистой энергии будет равно количеству поглощаемой лучистой энергии. Спектр излучения большинства твердых и жидких тел непрерывен. Эти тела испускают лучи всех длин волн от малых до больших. Спектр излучения газов имеет линейчатый характер. Газы испускают лучи не всех длин волн. Такое излучение называется селективным (избирательным). Излучение газов носит объемный характер.

Суммарное излучение с поверхности тела по всем направлениям полусферического пространства и по всем длинам волн спектра называется интегральным или полным лучистым потоком (Q).

Интегральный лучистый поток, излучаемый единицей поверхности по всем направлениям, называется излучательной способностью тела и обозначается

Е = dQ / dF, [вт/м²] (11.1) где dQ - элементарный лучистый поток, испускаемый элементом поверхности dF.

Каждое тело способно не только излучать, но и отражать, поглощать и пропускать через себя падающие лучи от другого тела. Если обозначить общее количество лучистой энергии, падающей на тело, через Q, то часть энергии, равная А, поглотится телом, часть, равная R, отразится, а часть, равная D, пройдет сквозь тело. Отсюда Q = Qa + Qr + Qd, (11.2)

или

A + R + D = 1. (11.3)

Величину А называют коэффициентом поглощения. Он представляет собой отношение поглощенной лучистой энергии ко всей лучистой энергии, падающей на тело. Величину R называют коэффициентом отражения. R есть отношение отраженной лучистой энергии ко всей падающей. Величину D называют коэффициентом проницаемости. D есть отношение прошедшей сквозь тело лучистой энергии ко всей лучистой энергии, падающей на тело. Для большинства твердых тел, практически не пропускающих сквозь себя лучистую энергию, А + R = 1.

Если поверхность поглощает все падающие на нее лучи, т. е. А = 1, R = 0 и D = 0, то такую поверхность называют абсолютно черной. Если поверхность отражает полностью все падающие на нее лучи, то такую поверхность называют абсолютно белой. При этом R = 1, А = О, D = 0. Если тело абсолютно проницаемо для тепловых лучей, то D = 1, R = 0 и A = 0. В природе абсолютно черных, белых и прозрачных тел не существует, тем не менее понятие о них является очень важным для сравнения с реальными поверхностями. Кварц для тепловых лучей непрозрачен, а для световых и ультрафиолетовых лучей прозрачен. Каменная соль прозрачна для тепловых лучей и непрозрачна для ультрафиолетовых лучей. Оконное стекло прозрачно для световых лучей, а для ультрафиолетовых и тепловых почти непрозрачно. Белая поверхность (ткань, краска) хорошо отражает лишь видимые лучи, а тепл

Дата добавления: 2013-12-13