
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модуль 1. Теоретические основы производственного менеджментата
|
|
|
|
Тема 7
Платежи с покрытием
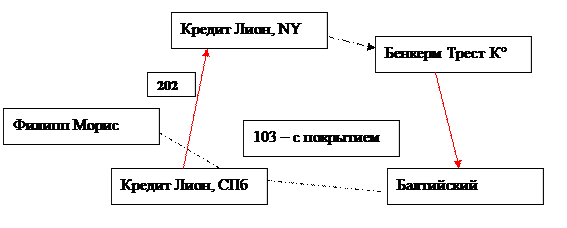
| FM 103 | FM 202 | FM 202 | FM 910 |
| Кредит лионе СПб | Кредит лионе СПб | Кредит Лионе,NY | Бенкерм Трест К° |
| Балтийский | Кредит Лионе,NY | Бенкерм Трест К° | Балтийский |
| ОТС 94292-02 | ОТС 94292-02 | ОТС 94292-02 | ОТС 94292-02 |
| Кредит Лионе,NY | Бэнкерс, NY | Кредит лионе СПб | Кредит лионе СПб |
| Бэнкерс, NY | Балтийский | Балтийский | Кредит Лионе,NY |
Платежи с покрытием
| Референс | |
| Связанный референс | |
| Банк-плательщик | |
| Б-кор отправителя | |
| Б.кор получателя | |
| Банк-посредник | |
| Банк-получателя | |
| Получатель |
Плоские волны в однородной изотропной среде
Плоские волны в среде без потерь
Рассмотрим однородную плоскую волну в среде без потерь. Свойства среды описываются абсолютными диэлектрической eа и магнитной mа проницаемостями. Векторы  и
и 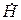 однородной плоской волны удовлетворяют уравнениям Максвелла без сторонних источников. Поэтому в однородной среде без потерь
однородной плоской волны удовлетворяют уравнениям Максвелла без сторонних источников. Поэтому в однородной среде без потерь  можно определить из системы уравнений Максвелла с вещественным волновым числом
можно определить из системы уравнений Максвелла с вещественным волновым числом 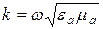 (
(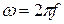 , где f – частота колебаний:
, где f – частота колебаний:
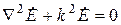 (1)
(1)

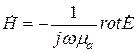 (2)
(2)
Поскольку в однородной плоской волне составляющие  могут зависеть только от одной координаты z, перпендикулярной плоским волновым поверхностям, то уравнение (1) примет вид:
могут зависеть только от одной координаты z, перпендикулярной плоским волновым поверхностям, то уравнение (1) примет вид:
 ,
,  ,
, 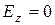 (3)
(3)
Дифференциальные уравнения второго порядка для  и
и 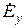 (3) имеют общие решения:
(3) имеют общие решения:
 ,
, 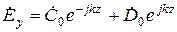 (4)
(4)
где  – произвольные постоянные интегрирования, представляющие собой комплексные амплитуды вектора поля при z = 0 (например,
– произвольные постоянные интегрирования, представляющие собой комплексные амплитуды вектора поля при z = 0 (например,  ).
).
Подставляя (4) в (2), определим составляющие 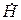 :
:
 ,
, 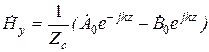 ,
, 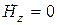 (5)
(5)

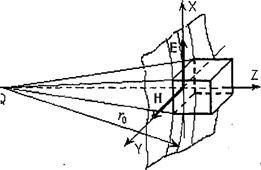 Предположим, что векторы
Предположим, что векторы  и
и  требуется знать только в области
требуется знать только в области  , размеры которой малы по сравнению с расстоянием до источника (
, размеры которой малы по сравнению с расстоянием до источника ( ). Введем декартову систему координат
). Введем декартову систему координат 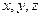 , ось
, ось 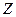 которой проведена вдоль радиуса-вектора, соединяющего середину вибратора
которой проведена вдоль радиуса-вектора, соединяющего середину вибратора 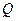 с точкой
с точкой 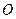 , принятой за начало координат (рис. 13). В пределах области
, принятой за начало координат (рис. 13). В пределах области  можно пренебречь изменением амплитуд векторов
можно пренебречь изменением амплитуд векторов  и
и  и, кроме того, считать, что их фазы зависят только от координаты
и, кроме того, считать, что их фазы зависят только от координаты 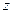 , т.е. считать, что
, т.е. считать, что  , a
, a  Запишем:
Запишем:
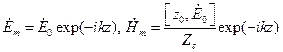 (6)
(6)
| С |
В (6) учтено, что векторы  и
и  перпендикулярны друг другу и направлению распространения волны (оси
перпендикулярны друг другу и направлению распространения волны (оси 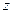 ). Ориентация векторов
). Ориентация векторов  и
и  относительно осей
относительно осей  и м зависит от ориентации источника, создающего поле. В общем случае эти векторы могут иметь как
и м зависит от ориентации источника, создающего поле. В общем случае эти векторы могут иметь как  -ю, так и
-ю, так и  -ю составляющие, связанные соотношениями
-ю составляющие, связанные соотношениями
 (7)
(7)
Поверхности равных фаз (ПРФ) в данном случае определяются уравнением 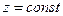 , т.е. представляют собой плоскости, перпендикулярные оси
, т.е. представляют собой плоскости, перпендикулярные оси 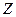 . Волну, ПРФ которой образуют семейство параллельных создаваемую ЭЭВ, в пределах области V можно рассматривать как плоскую волну плоскостей, называют плоской волной.
. Волну, ПРФ которой образуют семейство параллельных создаваемую ЭЭВ, в пределах области V можно рассматривать как плоскую волну плоскостей, называют плоской волной.
2. Свойства плоской волны в однородной изотропной среде
Исследуем основные свойства плоской волны, распространяющейся в безграничной однородной изотропной среде. Источники, создающие волну, находятся за пределами рассматриваемой области. Поэтому векторы  и
и  удовлетворяют однородным уравнениям Гельмгольца. Предположим, что поле не зависит от координат
удовлетворяют однородным уравнениям Гельмгольца. Предположим, что поле не зависит от координат  и
и  . Тогда уравнения принимают вид
. Тогда уравнения принимают вид
 (8)
(8)
где  . Решая уравнение для вектора
. Решая уравнение для вектора  , получаем
, получаем
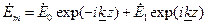 (9)
(9)
где  и
и 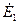 - некоторые векторные, в общем случае комплексные, постоянные.
- некоторые векторные, в общем случае комплексные, постоянные.
Считаем, когда потери в среде обусловлены только ее проводимостью, введем обозначение
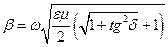 (10)
(10)
получаем  . Отметим, что
. Отметим, что 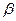 больше величины
больше величины  в среде без потерь с теми же значениями
в среде без потерь с теми же значениями 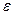 и
и 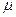 . Аналогично, обозначая
. Аналогично, обозначая
 (11)
(11)
получаем 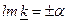 .
.
Рассмотрим волну в момент 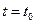 в точке
в точке  фаза напряженности электрического поля, соответствующего этой волне, равна
фаза напряженности электрического поля, соответствующего этой волне, равна 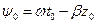 . В момент
. В момент  в точке
в точке 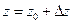 фаза той же функции равна
фаза той же функции равна  . Полагая
. Полагая  , приходим к соотношению
, приходим к соотношению  . Как видно, положительным приращениям
. Как видно, положительным приращениям 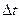 соответствуют положительные приращения
соответствуют положительные приращения  . Следовательно, такая волна распространяется в положительном направлении оси
. Следовательно, такая волна распространяется в положительном направлении оси 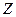 .
.
Предположим, что источник, создающий электромагнитное поле, расположен со стороны отрицательных значений 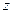 (рис.13). Так как среда считается безграничной и однородной, в рассматриваемой области пространства должна существовать только волна, распространяющаяся в положительном направлении оси
(рис.13). Так как среда считается безграничной и однородной, в рассматриваемой области пространства должна существовать только волна, распространяющаяся в положительном направлении оси 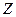 . Поэтому в первом слагаемом в формуле (11) в соответствии с выбором вида множителя
. Поэтому в первом слагаемом в формуле (11) в соответствии с выбором вида множителя 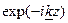 следует положить
следует положить
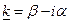 (12)
(12)
При выбранном значении  второе слагаемое в (9) описывает волну, распространяющуюся к источнику. Так как среда является однородной, то
второе слагаемое в (9) описывает волну, распространяющуюся к источнику. Так как среда является однородной, то 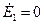 . Следовательно
. Следовательно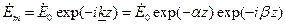 .
.
Аналогично, из уравнения Гельмгольца для вектора  находим, что
находим, что  , где
, где 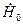 - некоторый постоянный (в общем случае комплексный) вектор. Непосредственно из уравнений Гельмгольца дополнительной информации о векторах
- некоторый постоянный (в общем случае комплексный) вектор. Непосредственно из уравнений Гельмгольца дополнительной информации о векторах  и
и  получить нельзя. Однако векторы
получить нельзя. Однако векторы  и
и  должны удовлетворять уравнениям Максвелла. Так как векторы
должны удовлетворять уравнениям Максвелла. Так как векторы  и
и  не зависят от переменных
не зависят от переменных  и
и  , то, проецируя указанные уравнения на ось
, то, проецируя указанные уравнения на ось 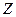 , замечаем, что
, замечаем, что 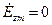 и
и  . Таким образом, и в случае
. Таким образом, и в случае 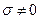 векторы
векторы  и
и  перпендикулярны направлению распространения волны. Такие волны называют поперечными. Проецируя затем уравнения на оси X и У, приходим к соотношениям
перпендикулярны направлению распространения волны. Такие волны называют поперечными. Проецируя затем уравнения на оси X и У, приходим к соотношениям 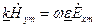 ,
,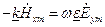 , из которых следует, что
, из которых следует, что
 (13)
(13)
где 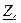 - характеристическое сопротивление волны (отношение поперечных к направлению распространения волны составляющих векторов
- характеристическое сопротивление волны (отношение поперечных к направлению распространения волны составляющих векторов  и
и  ). У волны, распространяющейся в среде с потерями,
). У волны, распространяющейся в среде с потерями, 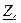 - комплексное число. В рассматриваемом случае
- комплексное число. В рассматриваемом случае
 (14)
(14)
где
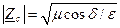 ;
;  (15)
(15)
В среде без потерь 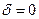 и
и 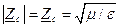 ;
; 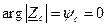 .
.
Таким образом, поле плоской волны в среде с проводимостью, отличной от нуля, определяется выражениями

 (16)
(16)
В среде без потерь  ,
, 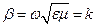
При изменении удельной проводимости от нуля до бесконечности угол  увеличивается от нуля до
увеличивается от нуля до  , а модуль
, а модуль 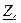 убывает от
убывает от  до нуля. Как видно, наличие потерь приводит к уменьшению абсолютной величины характеристического сопротивления, т.е. к увеличению
до нуля. Как видно, наличие потерь приводит к уменьшению абсолютной величины характеристического сопротивления, т.е. к увеличению 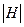 при заданном значении
при заданном значении 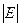 . Это обусловлено тем, что величина
. Это обусловлено тем, что величина  определяется как током проводимости, так и током смещения. В среде без потерь существуют только токи смещения. В среде с потерями при тех же значениях
определяется как током проводимости, так и током смещения. В среде без потерь существуют только токи смещения. В среде с потерями при тех же значениях  и
и 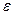 токи смещения остаются прежними, но к ним добавляются токи проводимости.
токи смещения остаются прежними, но к ним добавляются токи проводимости.
Проанализируем полученные результаты. Рассмотрим сначала случай, когда вектор  имеет лишь одну составляющую, например,
имеет лишь одну составляющую, например, 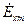 . Тогда вектор
. Тогда вектор  также будет иметь одну составляющую, перпендикулярную
также будет иметь одну составляющую, перпендикулярную  (в рассматриваемом примере
(в рассматриваемом примере 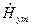 ). Считая вектор
). Считая вектор  вещественным (
вещественным ( ) и переходя к мгновенным значениям векторов
) и переходя к мгновенным значениям векторов  и
и  из получаем
из получаем

 (17)
(17)
В случае среды без потерь формулы принимают вид
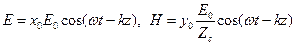 (18)
(18)
Из полученных формул видно, что поле плоской волны в однородной изотропной среде обладает следующими свойствами. Волна является поперечной. Комплексные амплитуды ( и
и  ) векторов
) векторов  и
и  всегда взаимно перпендикулярны, а в частном случае, когда вектор
всегда взаимно перпендикулярны, а в частном случае, когда вектор  имеет одну составляющую (например,
имеет одну составляющую (например,  ), взаимно перпендикулярны и их мгновенные значения. Поверхности равных фаз определяются уравнением
), взаимно перпендикулярны и их мгновенные значения. Поверхности равных фаз определяются уравнением 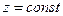 и представляют собой семейство плоскостей, перпендикулярных оси
и представляют собой семейство плоскостей, перпендикулярных оси 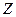 . Амплитуды векторов
. Амплитуды векторов  и
и  экспоненциально убывают вдоль оси
экспоненциально убывают вдоль оси 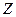 . Постоянную
. Постоянную  называют коэффициентом ослабления. В среде без потерь
называют коэффициентом ослабления. В среде без потерь  и
и


|
|
амплитуды векторов  и
и  не зависят от координат. При
не зависят от координат. При 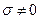 поверхности равных амплитуд (ПРА) совпадают с ПРФ. Волны, обладающие таким свойством, как и волны, амплитуды векторов
поверхности равных амплитуд (ПРА) совпадают с ПРФ. Волны, обладающие таким свойством, как и волны, амплитуды векторов  и
и  которых не зависят от координат, называют однородными. При
которых не зависят от координат, называют однородными. При 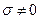 между векторами
между векторами  и
и  имеется фазовый сдвиг. Вектор
имеется фазовый сдвиг. Вектор  опаздывает по фазе относительно вектора
опаздывает по фазе относительно вектора  на угол
на угол  . В среде без потерь векторы
. В среде без потерь векторы  и
и  изменяются синфазно. При изменении
изменяются синфазно. При изменении 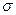 от нуля до бесконечности фазовый сдвиг возрастает от нуля до
от нуля до бесконечности фазовый сдвиг возрастает от нуля до  . На рис.14 и 15 показаны зависимости мгновенных значений векторов
. На рис.14 и 15 показаны зависимости мгновенных значений векторов  и
и  от времени
от времени 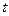 в некоторой фиксированной точке пространства (
в некоторой фиксированной точке пространства ( ) в среде с
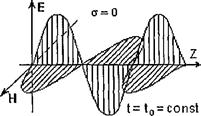
) в среде с 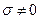 и в среде без потерь. На рис.16 и 17 показаны зависимости тех же величин от координаты
и в среде без потерь. На рис.16 и 17 показаны зависимости тех же величин от координаты 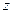 в некоторый фиксированный момент времени
в некоторый фиксированный момент времени 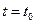 для случаев
для случаев 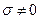 и
и  .
.
Фазовая скорость  плоской волны находится так же, как в случае сферической волны. Рассмотрим перемещение
плоской волны находится так же, как в случае сферической волны. Рассмотрим перемещение  ПРФ за время
ПРФ за время 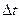 . В результате придем к равенству
. В результате придем к равенству  , из которого следует, что при
, из которого следует, что при 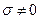
|
|
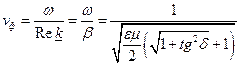 (19)
(19)
В среде без потерь 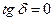 и
и 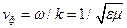 , т.е. равна скорости света в среде с теми же параметрами
, т.е. равна скорости света в среде с теми же параметрами 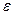 и
и 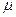 . Так как
. Так как 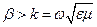 , то
, то  в среде с потерями меньше
в среде с потерями меньше  в среде без потерь с теми же
в среде без потерь с теми же 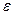 и
и 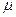 .
.
Параметр 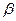 , определяющий фазовую скорость, называют коэффициентом фазы. При
, определяющий фазовую скорость, называют коэффициентом фазы. При 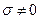 фазовая скорость зависит от частоты (
фазовая скорость зависит от частоты (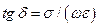 ): с увеличением последней она возрастает. Предельное значение
): с увеличением последней она возрастает. Предельное значение  при
при 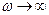 равно
равно 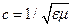 . Кроме того, величина
. Кроме того, величина  зависит от проводимости среды: при одинаковой частоте она будет меньше в среде с большей проводимостью.
зависит от проводимости среды: при одинаковой частоте она будет меньше в среде с большей проводимостью.
Длина волны при 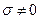
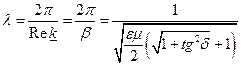 (20)
(20)
Она меньше длины волны в среде без потерь с теми же 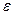 и
и 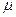 . Ее значение зависит от проводимости среды. При
. Ее значение зависит от проводимости среды. При  длина волны
длина волны  , где
, где 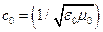 .
.
Распространение волны сопровождается переносом энергии. При 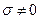 комплексный вектор Пойнтинга
комплексный вектор Пойнтинга
 (21)
(21)
содержит как действительную, так и мнимую часть. Это означает, что имеется как активный, так и реактивный поток энергии. Средняя за период плотность потока энергии экспоненциально убывает вдоль оси 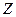 :
:
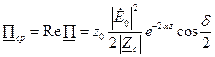 (22)
(22)
При  комплексный вектор Пойнтинга является чисто действительным и не зависит от координат:
комплексный вектор Пойнтинга является чисто действительным и не зависит от координат:
 (23)
(23)
Как видно, в этом случае имеется только активный поток энергии.
Возникновение реактивного потока энергии в среде с 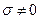 может быть объяснено следующим образом. При распространении электромагнитной волны в среде возникают электрические токи с плотностью
может быть объяснено следующим образом. При распространении электромагнитной волны в среде возникают электрические токи с плотностью 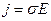 , на поддержание которых расходуется часть энергии волны. В свою очередь, возникшие в среде электрические токи, излучают.электромагнитное поле: создают вторичную плоскую волну, которая складывается с первичной, происходит непрерывный обмен энергией между волной и средой, что и приводит к возникновению реактивного потока энергии.
, на поддержание которых расходуется часть энергии волны. В свою очередь, возникшие в среде электрические токи, излучают.электромагнитное поле: создают вторичную плоскую волну, которая складывается с первичной, происходит непрерывный обмен энергией между волной и средой, что и приводит к возникновению реактивного потока энергии.
Скорость распространения энергии вычисляется по формуле и равна фазовой скорости:
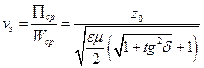 (24)
(24)
Как видно, при 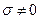 скорость распространения энергии зависит от частоты. В среде без потерь
скорость распространения энергии зависит от частоты. В среде без потерь 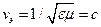 одинакова при любой частоте.
одинакова при любой частоте.
Характеристическое сопротивление волны 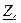 при
при 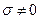 также зависит от частоты. Модуль
также зависит от частоты. Модуль 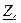 возрастает с увеличением
возрастает с увеличением  . Его предельное значение при
. Его предельное значение при  совпадает с характеристическим сопротивлением волны, распространяющейся в среде без потерь с теми же
совпадает с характеристическим сопротивлением волны, распространяющейся в среде без потерь с теми же 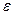 и
и 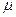 , т.е. равно
, т.е. равно  . Аргумент характеристического сопротивления
. Аргумент характеристического сопротивления  изменяется от
изменяется от  (при
(при 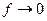 ) до нуля (при
) до нуля (при  ).
).
Из изложенного следует, что свойства плоской волны, распространяющейся в среде с проводимостью и в среде без потерь, различны. Основное отличие состоит в том, что в среде без потерь параметры плоской волны (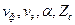 и др.) одинаковы при любых частотах, а в среде с проводимостью они зависят от частоты. Зависимость свойств волны от частоты называется дисперсией, а соответствующие среды - диспергирующими. Отметим, что среда может быть диспергирующей и при
и др.) одинаковы при любых частотах, а в среде с проводимостью они зависят от частоты. Зависимость свойств волны от частоты называется дисперсией, а соответствующие среды - диспергирующими. Отметим, что среда может быть диспергирующей и при  , если характеризующие ее параметры
, если характеризующие ее параметры 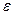 и
и 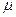 зависят от частоты.
зависят от частоты.
В общем случае вектор  имеет две составляющие
имеет две составляющие 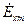 и
и  , между которыми возможен фазовый сдвиг. При этом вектор
, между которыми возможен фазовый сдвиг. При этом вектор  также будет иметь две составляющие
также будет иметь две составляющие  и
и 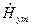 . Если составляющие вектора
. Если составляющие вектора  по осям
по осям  и
и 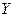 (
(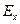 и
и  ) изменяются синфазно, то поворотом осей координат
) изменяются синфазно, то поворотом осей координат  и
и 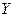 вокруг оси
вокруг оси 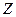 этот случай сводится к уже рассмотренному, когда вектор
этот случай сводится к уже рассмотренному, когда вектор  имеет одну составляющую. При наличии между составляющими
имеет одну составляющую. При наличии между составляющими 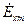 и
и  фазового сдвига, не равного
фазового сдвига, не равного  , где
, где  - целое число, волна имеет некоторые особенности, например при
- целое число, волна имеет некоторые особенности, например при 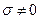 мгновенные значения векторов
мгновенные значения векторов  не являются взаимно перпендикулярными. Перечисленные выше остальные свойства плоской волны имеют место и в этом случае.
не являются взаимно перпендикулярными. Перечисленные выше остальные свойства плоской волны имеют место и в этом случае.
3. Волны в диэлектриках
В диэлектриках 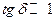 , поэтому можно приближенно положить
, поэтому можно приближенно положить  . Тогда получаем:
. Тогда получаем:  (25)
(25)
Находим: (26)
(26)
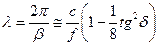 (27)
(27)
 (28)
(28)
Из полученных результатов следует, что параметры волны (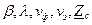 ), распространяющейся в реальном диэлектрике, мало отличаются от ее параметров в среде без потерь с теми же
), распространяющейся в реальном диэлектрике, мало отличаются от ее параметров в среде без потерь с теми же 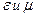 . Коэффициент ослабления
. Коэффициент ослабления  является малой величиной и в первом приближении не зависит от частоты. Дисперсионные свойства проявляются незначительно.
является малой величиной и в первом приближении не зависит от частоты. Дисперсионные свойства проявляются незначительно.
4. Волны в проводниках
В проводниках (например, в металлах) 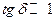 . Поэтому в выражениях для
. Поэтому в выражениях для  можно пренебречь единицей по сравнению с
можно пренебречь единицей по сравнению с  . В результате получим
. В результате получим
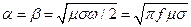 (29)
(29)
Постоянные  нелинейно зависят от частоты. Следовательно, свойства волны на разных частотах будут существенно различаться. Формулы для фазовой скорости, длины волны и характеристического сопротивления в этом случае принимают вид
нелинейно зависят от частоты. Следовательно, свойства волны на разных частотах будут существенно различаться. Формулы для фазовой скорости, длины волны и характеристического сопротивления в этом случае принимают вид
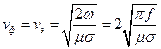 (30)
(30)
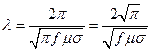 (31)
(31)
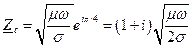 (32)
(32)
Сравним параметры плоских волн, распространяющихся в вакууме и в меди ( ) на частоте 1 Мгц.
) на частоте 1 Мгц.
в вакууме: в металле:
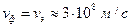 ;
;  ;
;
 м;
м;  м;
м;
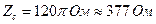 ;
; 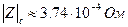 .
.
5. Затухание волн
Коэффициент ослабления  волны, распространяющейся в проводнике, большая величина. Поэтому амплитуды векторов поля резко уменьшаются вдоль направления распространения: волна быстро затухает. Пусть амплитуда напряженности электрического поля в точке с координатой
волны, распространяющейся в проводнике, большая величина. Поэтому амплитуды векторов поля резко уменьшаются вдоль направления распространения: волна быстро затухает. Пусть амплитуда напряженности электрического поля в точке с координатой 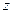 равна
равна 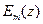 , а амплитуда в точке с координатой
, а амплитуда в точке с координатой 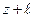 равна
равна 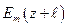 . Отношение
. Отношение
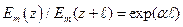 (33)
(33)
показывает, во сколько раз уменьшилась амплитуда волны при прохождении ею расстояния  .
.
Затухание измеряют в неперах (Нп) и децибелах (дБ). Затухание в неперах определяют как натуральный логарифм отношения (33) 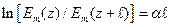 . Затухание в децибелах определяют как двадцать десятичных логарифмов того же отношения:
. Затухание в децибелах определяют как двадцать десятичных логарифмов того же отношения: 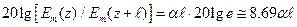 , т.е.
, т.е. 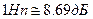 . Коэффициент
. Коэффициент  , таким образом, определяет затухание волны при прохождении ею пути в один метр и измеряется в неперах на метр (Нп/м).
, таким образом, определяет затухание волны при прохождении ею пути в один метр и измеряется в неперах на метр (Нп/м).
Вычислим затухание волны, распространяющейся в меди, при частоте в 1 Мгц. Коэффициент ослабления  Нп/м. Это означает, например, что при прохождении волной расстояния в один миллиметр ее амплитуда уменьшается в
Нп/м. Это означает, например, что при прохождении волной расстояния в один миллиметр ее амплитуда уменьшается в  раз, т.е. примерно в 2,67 миллиона раз. Приведенный пример показывает, что переменное электромагнитное поле на частотах радиотехнического диапазона практически не проникает в глубь проводника.
раз, т.е. примерно в 2,67 миллиона раз. Приведенный пример показывает, что переменное электромагнитное поле на частотах радиотехнического диапазона практически не проникает в глубь проводника.
6. Глубина проникновения
Расстояние  , при прохождении которого электромагнитное поле ослабевает в
, при прохождении которого электромагнитное поле ослабевает в 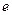 раз, называют глубиной проникновения поля в среду. На расстоянии
раз, называют глубиной проникновения поля в среду. На расстоянии  ослабление составляет 1 Нп, т.е.
ослабление составляет 1 Нп, т.е. 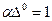 и, следовательно,
и, следовательно,
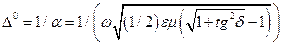 (34)
(34)
В случае металла выражение (34) упрощается:
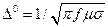 (35)
(35)
Как видно из формулы (35), глубина проникновения от частоты: чем больше частота, тем меньше  .
.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 406; Нарушение авторских прав?; Мы поможем в написании вашей работы!