
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Работа и мощность
|
|
|
|
Принцип Даламбера для материальной точки
Принцип Даламбера в его современном истолковании эквивалентен второму закону Ньютона и принципу освобождаемости от связей, т.е. равнозначен уравнению, но записывается и формулируется в другом виде, удобном для многих приложений. Силой инерции называется вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению:
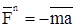 ; модуль силы:
; модуль силы: 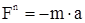 .
.
Из уравнения  находим F + R +(-ma) = 0
находим F + R +(-ma) = 0
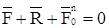
Последнее равенство выражает принцип Даламбера и по своему виду совпадает с необходимым и достаточным условием равновесия системы сходящихся сил: если к заданным силам и реакциям связей, действующим на движущуюся несвободную точку, мысленно добавить силу инерции точки, то получим уравновешанную систему сил. Сила инерции на самом деле к точке не приложена, иначе точка находилась бы в равновесии  , а на самом деле она движется с ускорением
, а на самом деле она движется с ускорением 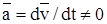 , т.е.
, т.е. 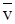 - величина переменная. Применение принципа Даламбера позволяет при решении динамических задач использовать уравнения равновесия. Такой прием решения задач динамики называют методом кинетостатики.
- величина переменная. Применение принципа Даламбера позволяет при решении динамических задач использовать уравнения равновесия. Такой прием решения задач динамики называют методом кинетостатики.
Выражение dA = F ·cosφ·ds называют элементарной работой силы 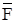 на бесконечно малом (элементарном) перемещении ds. Угол φ составляет направление силы с направлением элемента траектории ds, совпадающим с направлением касательной к траектории.
на бесконечно малом (элементарном) перемещении ds. Угол φ составляет направление силы с направлением элемента траектории ds, совпадающим с направлением касательной к траектории.
Чтобы получить работу силы на конечном перемещении, надо взять интеграл от выражения элементарной работы силы. Получаем выражение работы силы:
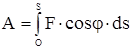 .
.
Работа силы, постоянной по модулю и направлению, не зависит от формы и длины нуги и равна произведению модуля силы на проекцию пути на направление силы. В частности, работа силы тяжести не зависит от траектории тела и равна произведению модуля силы тяжести тела на изменение уровня тела над поверхностью Земли.
Единицы измерения работы в системе СИ: [А] = 1 Нм = 1 Дж (джоуль), а в технической системе единиц: [А] =1 кгс 1 м = 1 кгс м.
1 кДж (килоджоуль) = 1000 Дж. В технике пользуются также кВт ч (киловатт-час): I кВт ч = 3600 Дж. Так как 1 кгс = 9,81 Н, а 1 Н = 0,102 кгс, то имеем 1 кгс м = 9,81 Н м = 9,81 Дж.
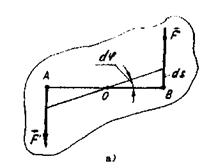
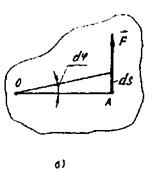
Пусть пара сил, приложенная к твердому телу, действует в плоскости, перпендикулярной к оси вращения этого тела (Рисунок 17. а).
|
|
Рис 17.
Тогда при повороте на элементарный (малый) угол dφ силы пары произведут работу:
dA = F · ds + F · ds = 2 F · ds
где ds - величина перемещения точки приложения каждой силы. Но ds = 0,5 АВ· dφ, поэтому dA = (F · АВ) dφ. Момент пары М = F · АВ. Следовательно, для вращательного движения тела имеет место формула
dA = M · dφ
Итак, элементарная работа пары сил, вращающей твердое тело вокруг неподвижной оси, перпендикулярной к плоскости пары, равна произведению момента пары на элементарный угол поворота тела При конечном повороте тела имеем
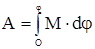
Если М = const, то 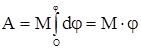
Аналогично получаем элементарную работу силы, приложенной к твердому телу, имеющему неподвижную ось крашения (Рисунок 17. б):
dA = F · ds; ds = OA· dφ, поэтому dA = (F · OA) dφ, но, поскольку момент силы F относительно оси вращения тела M1(F) = F · OA, то
 и
и 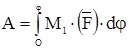
Если момент силы относительно оси /вращения постоянен, то:
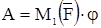
Элементарной работой системы сил F1,F2,…Fn называют алгебраическую сумму элементарных работ всех составляющих сил.
Работа равнодействующей системы сходящихся сил на некотором перемещении равна сумме работ всех составляющих сил на том же перемещении.
Мощность. Мощностью называют работу силы в единицу времени
P = dA/dt = F cosφ · ds/dt= F · cosφ · v,
т.е. мощность силы равна скалярному произведению силы на скорость ее точки приложения. Единица измерения мощности в системе СИ:
[Р] = [F][v]; 1 Вт (ватт) = 1 Дж/с.
В технической системе единиц за единицу мощности берут 1 кгсм/с. В технике за единицу измерения мощности часто принимают 1 л.с. (лошадиная сила) = 75 кгсм/с = 736 Вт.
Определим мощность при вращательном движении тела:
P = dA/dt = d(Mφ)/dt = M · ω
т.е. при вращательном движении тела мощность равна произведению вращающего момента на угловую скорость.
Но ω = π · n/30, где n - частота вращения, об/мин, следовательно:
P = M · π · n/30
отсюда M = 30P/ π · n
Если мощность Р постоянна, то вращающий момент обратно пропорционален частоте вращения тела.
Коэффициентом полезного действия (КПД) механизма называют отношение полезной работы к работе движущих сил:
η = Aп.c. /Aд.с.
Полезная работа Ап.с. расходуется на преодоление работы сил полезных сопротивлений. Так как Ап.с. < Ад.с., то η < 1. Чем больше Ап.с, тем меньше вредное сопротивление и тем КПД ближе к единице.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 1123; Нарушение авторских прав?; Мы поможем в написании вашей работы!