Растяжение и сжатие, смятие и сдвиг

2.4.1 Растяжение (сжатие).

Растяжением (сжатием) называется такой вид деформации, при котором в поперечном (перпендикулярном оси) сечении стержня возникает только продольная растягивающая (сжимающая) сила. Модель растягиваемого стержня широко используется в расчетах болтов, ремней передач, стержней ферм, лопаток турбин и др. Для определения величины продольной силы F_z используют метод сечений (Рисунок 48).

Продольная сила F_z, приложенная в центре тяжести произвольного сечения стержня, является равнодействующей внутренних сил dF_z =σdA, действующих на бесконечно малые площадки поперечного сечения площадью А:

Из этого уравнения нельзя найти закон распределения нормальных напряжений по поперечному сечению. Однако, если предположить, что в пределах действия закона Гука плоские поперечные сечения стержня смещаются при растяжении параллельно начальным положениям, оставаясь плоскими, то нормальные напряжения во всех точках сечения должны быть одинаковыми, т.е. σ= соnst, тогда F_z = σA и σ = F_z/A.

Таким образом, нормальное напряжение в поперечном сечении стержня при растяжении равно отношению продольной силы к площади сечения.

При сжатии стержня напряжения имеют отрицательный знак: нормальная сила направлена в тело стержня. Нормальные напряжения в элементах конструкций не должны превышать допускаемые напряжения:

Данное условие прочности при растяжении позволяет решать задачи расчета элементов конструкций на прочность:

1) При известных размерах поперечного сечения детали А и известном допускаемом напряжении [σ] определяют допускаемые нагрузки: .

Рис 48.

2) Определяют площадь поперечного сечения по заданной силе и допускаемому напряжению.

, для круга: ;

3) При известной силе и площади поперечною сечения детали определяют напряжения и проверяют, не превышают ли они допускаемые:

.

Итак, напряжения при растяжении (сжатии) 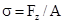. С другой стороны, согласно закона Гука в пределах малых деформаций напряжения прямо пропорциональны вызываемой ими относительной деформации. Так как относительная деформация , тогда 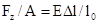, откуда 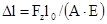. То есть, в пределах малых деформаций абсолютное продольное удлинение прямо пропорционально силе F_z и первоначальной длине стержня l_o и обратно пропорционально модулю упругости E и площади поперечного сечения А. Произведение ЕА называется жесткостью сечения стержня при растяжении (сжатии).

В некоторых случаях при работе конструкции на сжатие работоспособность ее определяю! не величиной допускаемой нагрузки или допускаемого напряжения, а величиной допускаемой деформации. В том случае находят фактическое абсолютное удлинение и сопоставляют его с допускаемым, такие расчеты называются расчетами на жесткость:

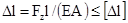- сосредоточенная нагрузка или

- распределенная нагрузка.

Опыты показывают, что удлинение стержня в осевом направлении при растяжении сопровождается уменьшением его поперечных размеров, т.е. наряду с продольной возникает поперечная деформация стержня.

2.4.2 Смятие.

Если два тела подвергаются сжимающей нагрузке и соприкасаются между собой, то общие поверхности соприкосновения называют поверхностями контакта. На поверхностях контакта возникают напряжения смятия. При расчете на смятие допускают, что силы взаимодействия равномерно распределены по поверхности соприкосновения и в каждой точке нормальны к пой поверхности, т.е. возникают нормальные напряжения. Элементарная сила на элементарной площадке . Полная сила .

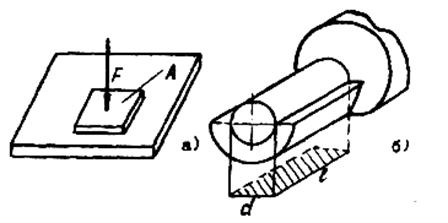
Тогда, основное условие прочности на смятие 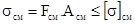. Допускаемое напряжение на смятие 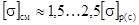(Рисунок 49. а).

Если контакт деталей осуществляется по поверхности полуцилиндра, то площадь смятия определяется как проекция поверхности контакта на диаметральную плоскость (Рисунок 49. б).

Рис 49.

Для многих деталей контакт происходит не по площади, а по линии или точке. В этом случае напряжения смятия определяют по теории контактных напряжений.

Под действием нагрузки, прижимающей тела друг к другу в направлении по нормали к их поверхностям, в поверхностных слоях материала деталей возникают местные деформации и контактные напряжения. Давления по площадке контакта распределяются по эллиптическому закону. Максимальные контактные напряжения возникают в центре (точке контакта) (Рисунок 50. а). Контактные напряжения определяются по формуле Беляева-Герца

μ - коэффициент Пуассона;

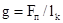- интенсивность силы давления по длине контактной линии;

- приведенный модуль упругости материалов, при ; ;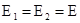

Рис 50.

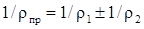- приведенная кривизна поверхностей в месте контакта (Рисунок 50. а).

Знак «-» - одна из поверхностей вогнута. Если одна поверхность прямолинейна (т.е. р₂ = ∞), то ρ_пр = ρ₁, (Рисунок 50. б, в).

2.4.3 Сдвиг.

Сдвиг - это деформация, вызываемая противоположно направленными силами, лежащими в близких параллельных плоскостях. Результатом сдвига является срез, например, резание материала ручными или механическими ножницами (Рисунок 51).

Рис 51.

При сдвиге происходит перекашивание прямых углов элементарных параллелепипедов. Степень деформирования определяется величиной, которая называется абсолютной деформацией (абсолютным сдвигом). Деформация сдвига, доведенная до разрушения, называется срезом. Отношение абсолютного сдвига к расстоянию между сдвигающимися сечениями - относительная деформация (относительный сдвиг) .

В виду малости величин (Рисунок 51. б). Величина у - относительный сдвиг или угол сдвига.

Внутренние силы, уравновешивающие внешние силы, приложенные к отмеченной части, называются поперечными (перерезывающими силами) F_Qy, т.к. они действуют перпендикулярно оси стержня.

Поперечная сила складывается как сумма элементарных внутренних сил

(Рисунок 51. в).

Если принять допущение, что касательные напряжения распределяются по сечению равномерно и равны, т.е. .

Дата добавления: 2013-12-14