Напряжения при кручении

Кручение - это деформация, вызываемая действием пар сил, лежащих в параллельных плоскостях, перпендикулярных оси стержня. На основании опытных данных известно:

1) если на поверхность вала нанести сетку в виде квадратиков, то при приложении вращающею момента Т квадраты перекашиваются, обращаясь в ромбы т.е. подвергаются деформации сдвига (Рисунок 54. а);

2) образующие поворачиваются на один и тот же угол у. При малых деформациях они остаются прямыми (при больших - винтовыми);

3) расстояния между поперечными сечениями dz практически не изменяются, следовательно, в направлении параллельном оси стержня z нормальное напряжение отсутствует σ = 0;

4) сечения круглые и плоские до деформации остаются плоскими, но поворачиваются вокруг оси на некоторый угол, называемый углом закручивания ф. Величина этого угла пропорциональна величине вращающего момента и расстоянию между сечениями.

5) радиусы поперечных сечений при деформации остаются прямыми.

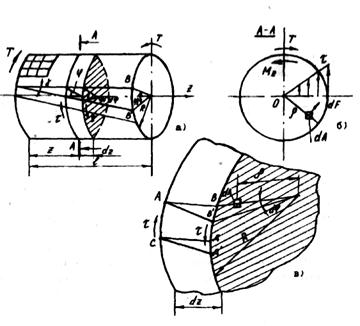
Рис 54.

На основании этих наблюдений в расчетах предполагают, что сечения плоские до закручивания остаются плоскими после закручивания; расстояния между поперечными сечениями не изменяются, а радиусы поперечных сечений при деформации остаются прямыми.

В соответствии с этими гипотезами материал в поперечных сечениях подвергается чистому сдвигу, т.е. при кручении стержня круглого поперечного сечения по площадкам, перпендикулярным к оси вала, возникают только касательные напряжения (Рисунок 54. б).

Разрежем мысленно скручиваемый вал на расстоянии 2 и отбросим правую часть. Левая оставшаяся часть должна находиться в равновесии под действием вращающего момента Т и крутящего момента М_z от внутренних сил dF, которые заменяют действие отброшенной части (Рисунок 54. б):

М_z = Т.

Выделим элементарную площадку dA. Сила, приложенная к ней будет: ;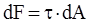

;

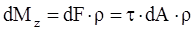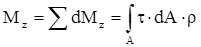. (2.1)

Из полученного уравнения величину касательных напряжений найти не можем, т.к. не знаем как они распределяются но сечению, то есть, задача статически неопределимая. Для раскрытия статической неопределимости обратимся к рассмотрению упругих деформаций вала. Рассмотрим два сечения на элементарном расстоянии dz (Рисунок 54. в).

Деформации:

Абсолютного сдвига .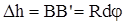

Относительный сдвиг .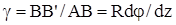

По закону Г ука при сдвиге касательные напряжения в точке В 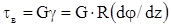; 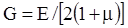- модуль упругости второго рода, для стали .

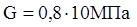Касательные напряжения в любой площадке на расстоянии ρ:

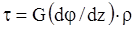(2.2)

Подставим уравнение (2.2) в (2.1):

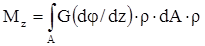
При интегрировании по площади ни φ, ни z не изменяются, то есть

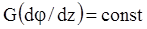
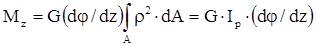
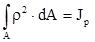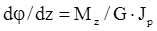так как ; или (2.3)

Подставим уравнение (2.3) в (2.2): 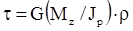. Наибольшие напряжения будут пр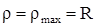и и ; ,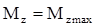

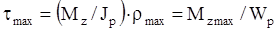где 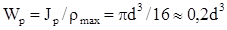- полярный момент сопротивления круглого вала или момент сопротивления сечения при кручении. Основное условие прочности при кручении:

(2.4)

Допускаемое напряжение при кручении: .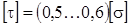

Тогда диаметр вала из условия прочности .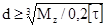

2.5.2 Деформации при кручении.

Деформации мри кручении характеризуются углом поворота одного сечения относительно другою или углом закручивания.

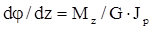откуда .

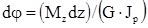На длине l угол закручивания будет

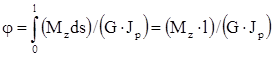- закон Гука при кручении, (2.5)

где 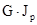- жесткость сечения стержня при кручении.

Принимая 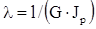- крутильная податливость стержня, получим, что .

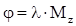2.5.3 Условие жесткости скручиваемого вала.

Если площадь сечения изменяется по длине стержня ступенчато, а М скачкообразно, то полный угол закручивания определяют, суммируя углы закручивания по участкам, в пределах которых М_кр и J_p постоянны. Тогда условие жесткости скручиваемого вала:

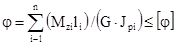(рад),

или ,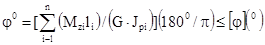

или .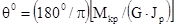

Угол закручивания на единицу длины бруса называют относительным углом закручивания 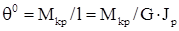рад/м.

Допускаемое значение относительного угла закручивания зависит от конструкции.

Диаметр вала с учетом обеспечения жесткости:

.

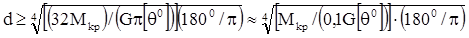Таким образом, размеры вала следует определять не только из условия прочности (2.4). но и из условия жесткости (2.5).

2.5.4 Напряжения при изгибе.

Чистым называют такой изгиб, при котором в сечениях изгибаемой балки возникают только нормальные напряжения. На основании опытных данных известно (Рисунок 55):

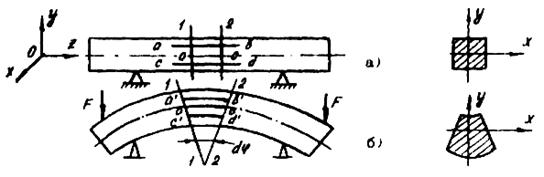
Рис 55.

1) При изгибе одни волокна растягиваются аb, другие сжимаются cd. Следовательно, имеется слой волокон, который отделяет сжатую зону от растянутой (Рисунок 55. б).

2) Изменяются и поперечные размеры балки. Ширина балки внизу увеличивается (сжаты продольные волокна, а поперечные волокна растянуты), вверху ширина балки уменьшается (растянуты продольные волокна, а поперечные сжаты).

3) Вертикальные линии 1-1, 2-2 остаются прямыми, но наклоняются друг к другу на некоторый угол dφ.

4) Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью (ось х).

5) Нейтральная ось х и ось у являются главными центральными осями.

Ограничения при расчете: Рассматривают участок, где балка подвергается чистому изгибу (II участок).

Балка имеет хотя бы одну плоскость симметрии, и все внешние силы лежат в этой плоскости, такой изгиб называется плоским, т.к. изогнутая ось лежит в плоскости действия силы.

Материал балки подчиняется закону Гука, и модуль упругости при растяжении и сжатии одинаков.

Опытные наблюдения дают основания для принятия следующих гипотез: Сечения после изгиба остаются плоскими, но поворачиваются вокруг нейтральной оси на угол dφ. Волокна не оказывают давления друг на друга (σ_y и σ_z = 0), следовательно, подвергаются простому растяжению или сжатию.

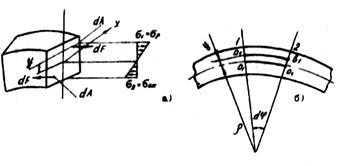
Рис 56.

Рассмотрим сечение балки. Выделим элементарные площадки dА сверху и снизу от нейтральной оси х на расстоянии у (Рисунок 56. а).

Элементарная сила (сверху растягивающая, снизу - сжимающая) будет равна dF = σdA, где σ - нормальное напряжение при растяжении.

Элементарный изгибающий момент от этой силы:

.

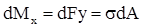Изгибающий момент равен сумме элементарных моментов, т.е. интегралу по площади 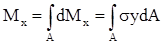. (2.6)

Из полученного уравнения величину М_у найти не можем, т.к. не знаем как распределяются напряжения по сечению, т.е. задача статически неопределима. Обратимся к рассмотрению деформаций (Рисунок 56. б), ρ - радиус кривизны нейтрального слоя. Длина волокна до изгиба ab = OO = l. Длина нейтрального слоя после изгиба остается постоянной 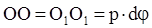.Длина волокна аb после изгиба увеличилась 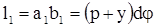. Абсолютное удлинение 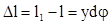. Относительное удлинение .

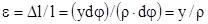По закону Гука 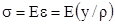. (2.7)

Подставим (2.7) в (2.6): ,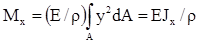

где 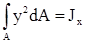- осевой момент инерции, или

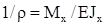- кривизна балки. (2.8)

Подставим уравнение (2.8) в (2.7): 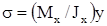. Из этой формулы следует ряд важных выводов:

- центр тяжести стержня является началом координат для анализа напряжений и приведения внешних сил;

- напряжения изгиба зависят от значений M_x, J_x и координаты рассматриваемой точки;

- напряжения в любой точке, лежащей на одинаковом расстоянии от нейтральной линии, равны между собой;

- нормальные напряжения не зависят от модуля упругости стержня, например, два конструктивно одинаковых стержня из стали и и титанового сплава) при рамной внешней нагрузке имеют одинаковые напряжения в соответствующих точках сечений.

Основное условие прочности при изгибе:

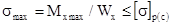(2.4)

При проектом расчете на прочность при изгибе определяют необходимые размеры сечения, например, для круглою сечения

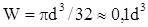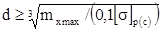; , мм.

Для прокатных профилей после расчета W_x подбирают номер профиля по справочным таблицам.

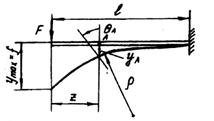
2.5.5 Деформации и перемещения при изгибе.

Под действием внешних сил, расположенных перпендикулярно к оси балки в плоскости симметрии, балка будет искривляться. Первоначальная прямая ось балки искривляется, превращаясь в кривую линию, которую называют изогнутой осью или упругой линией балки (Рисунок 57). Ранее было получено, что кривизна балки 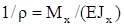. 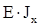- жесткость при изгибе.

Вертикальное перемещение называется прогибом

;

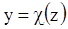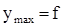
Поперечные сечения поворачиваются вокруг нейтральной оси. Угол поворота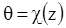

Рис 57.

Итак, перемещения балки характеризуются двумя параметрами:

1) 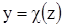- линейные перемещения (прогибы),

2) 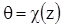- угловые перемещения.

Причем, производная от прогиба по абсциссе равна тангенсу угла поворота поперечного сечения

или 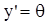, т.к.

tgθ = θ (при малых значениях θ). Вторая производная от прогиба равна кривизне балки .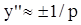

2.6 Основы теории напряженного состояния.

Если элемент материала, взятый из окрестности точки, подвергать растяжению либо сжатию в двух или грех направлениях, то материал будет находиться в условиях сложного напряженною состояния.

Различают следующие виды напряженного состояния:

1) Линейное (одноосное).

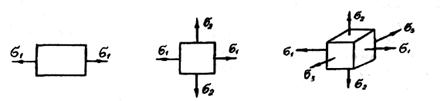
2) Плоское (двухосное).

3) Объемное (трехосное) (Рисунок 58).

Рис 58.

2.7 Прочность при переменных напряжениях.

Дата добавления: 2013-12-14