
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрическая интерпретация задачи производственного планирования
|
|
|
|
Задачи производственного менеджмента во многих случаях оказываются ассоциированными с задачами распределительного типа, т.е. с задачами, в которых требуется распределить ограниченные ресурсы по нескольким видам производственной деятельности.
Рассмотрим следующую ситуацию, получившую название задачи производственного планирования. Пусть из технологических соображений известен перечень продуктов, которые предприятие может производить без дополнительных капиталовложений. Кроме того, известны вид и количество ресурсов отпущенных предприятию для производственного потребления и структура материальных затрат и доходов. В этих условиях перед предприятием стоит задача выбора плана производства, обеспечивающего получение максимальной прибыли.
Перейдем к построению математической модели рассмотренной ситуации. Будем считать, что предприятие может производить n различных продуктов (j = 1,..., n). Количество j-го продукта выпускаемого по плану, обозначим через xj. В этом случае план производства может быть описан с помощью вектора 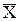 = (X1, X2,..., Xn). Предположим, что предприятие располагает для организации производственного процесса m видами различных ресурсов (i = 1,..., m). Количество ресурса i-го вида, отпущенное предприятию для потребления обозначим через bi. Количество ресурса i-го вида, расходуемое предприятием на производство единицы j-го продукта, обозначим через aij, а прибыль, от производства единицы продукции j-го вида через cj.
= (X1, X2,..., Xn). Предположим, что предприятие располагает для организации производственного процесса m видами различных ресурсов (i = 1,..., m). Количество ресурса i-го вида, отпущенное предприятию для потребления обозначим через bi. Количество ресурса i-го вида, расходуемое предприятием на производство единицы j-го продукта, обозначим через aij, а прибыль, от производства единицы продукции j-го вида через cj.
Тогда, в принятых нами обозначениях, задача выбора плана производства, обеспечивающего получение максимальной прибыли может быть сформулирована как математическая задача в следующем виде:
Найти вектор-план  =(X1,X2,...,Xn), удовлетворяющий системе ограничений
=(X1,X2,...,Xn), удовлетворяющий системе ограничений
 i=1,...,m,
i=1,...,m,
Xj 0,
0, 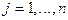
и доставляющий целевой функции задачи
F(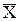 ) =
) = 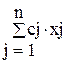
максимальное значение.
Пример 1. Предприятие производит два вида продукции А1, А2, используя сырье трех типов: S1, S2, S3. Нормы расхода сырья каждого типа на единицу продукции, их наличие в распоряжении предприятия, а также прибыль от реализации единицы продукции приведены в таблице 1. Требуется составить такой план выпуска продукции, при котором прибыль предприятия от ее реализации является максимальной.
Таблица 1
| Вид | Норма расхода сырья на единицу продукции | Наличие | |
| сырья | А1 | А2 | сырья |
| S1 | |||
| S2 | |||
| S3 | |||
| Прибыль от единицы продукции |
Математическая модель данной задачи может быть записана следующим образом. Определить объемы производства продукции вида А1 и А2, при которых достигается максимум целевой функции
F( )= 3×X1 + 4×X2
)= 3×X1 + 4×X2
при ограничениях
X1 + X2 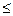 5
5
2×X1 + X2 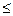 9
9
X1 + 2×X2 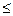 7
7
X1,X2  0,
0,
где X1 и X2 - количество единиц продукции вида А1 и А2.
С формальных позиций данная модель является линейной потому, что все входящие в нее функции линейные. Так как модель содержит только две переменные, задачу можно решить графически.
Первый шаг, при использовании графического метода, заключается в геометрическом представлении допустимых решений, т.е. построении области, в которой одновременно выполняются все ограничения модели. Искомая область (пространство) решений показана на рис. 1.
 Рис. 1. Геометрическая интерпретация задачи производственного планирования
Рис. 1. Геометрическая интерпретация задачи производственного планирования
Пространство решений содержит бесконечное число точек. Известно, что направление возрастания целевой функции модели определяется вектором-градиентом, т.е. вектором с координатами (3;4) – [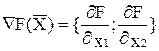 = {3, 4}]. На рис.1 это направление показано стрелкой. Чтобы найти оптимальное решение, следует перемещать прямую характеризующую прибыль (линию уровня целевой функции) в направлении вектора-градиента до тех пор, пока она не сместится в область недопустимых решений. Из рис.1 видно, что оптимальному решению соответствует точка С с координатами (3;2). Полученное решение означает, что объем производства продукции А1 равен трем единицам, а продукции А2 равен двум единицам. Прибыль от реализации составит 17 денежных единиц. Заметим, что оптимальному решению всегда может быть поставлена в соответствие одна из допустимых угловых точек пространства решений (на рис.1 это точки А,B,С,D,Е). Какая из этих точек окажется оптимальной, зависит от наклона линии уровня целевой функции, т.е. от коэффициентов целевой функции.
= {3, 4}]. На рис.1 это направление показано стрелкой. Чтобы найти оптимальное решение, следует перемещать прямую характеризующую прибыль (линию уровня целевой функции) в направлении вектора-градиента до тех пор, пока она не сместится в область недопустимых решений. Из рис.1 видно, что оптимальному решению соответствует точка С с координатами (3;2). Полученное решение означает, что объем производства продукции А1 равен трем единицам, а продукции А2 равен двум единицам. Прибыль от реализации составит 17 денежных единиц. Заметим, что оптимальному решению всегда может быть поставлена в соответствие одна из допустимых угловых точек пространства решений (на рис.1 это точки А,B,С,D,Е). Какая из этих точек окажется оптимальной, зависит от наклона линии уровня целевой функции, т.е. от коэффициентов целевой функции.
Основы анализа на чувствительность (анализ модели после нахождения оптимального решения)
После того как оптимальное решение получено выявляется его чувствительность к определенным изменениям исходной модели. В нашей задаче, например, могут представить интерес вопросы о том, как повлияет на оптимальное решение изменение запасов сырья и изменение прибыли от единицы продукции.
В связи с этим представляется логичным выяснить:
1. На сколько можно увеличить запас некоторого вида сырья для улучшения полученного оптимального значения целевой функции?
2. На сколько можно снизить запас некоторого вида сырья при сохранении полученного оптимального значения целевой функции?
3. Увеличение объемов какого вида сырья наиболее выгодно?
4. Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?
Прежде чем ответить на первые два вопроса, классифицируем ограничения на активные и неактивные. Прямая, представляющая активное ограничение, должна проходить через оптимальную точку. В противном случае соответствующее ограничение будет неактивным. На рис.1 активными ограничениями являются (1) и (3), т.е. те, которые лимитируют запасы сырья S1 и S3.
Если некоторое ограничение является активным, логично отнести соответствующее сырье к разряду дефицитных, т.к. оно расходуется полностью. Сырье, с которым ассоциируется неактивное ограничение, следует отнести к разряду недефицитных, так как оно имеется в некотором избытке. В нашей задаче используемое сырье S1 и S3 является дефицитным.
Рассмотрим вначале сырье S1 (ограничение 1). Из рис.1 видно, что при увеличении запаса этого вида сырья прямая (1) (отрезок СД) перемещается вверх параллельно самой себе, постепенно стягивая в точку треугольник СКД. В точке К становятся активными ограничения (2) и (3). Оптимальному решению при этом будет соответствовать точка К, в которой ограничение (1) становится неактивным. Поэтому дальнейший рост запаса сырья S1 не следует увеличивать сверх того предела, когда ограничение становится неактивным (избыточным).
Этот предельный уровень определяется путем подстановки координат точки К(11/3;5/3) в левую часть ограничения (1). В результате получим
1×11/3 + 1×5/3 = 16/3,
F(K) = 3×11/3 + 4×5/3 = 53/3.
Аналогично рассматривается вопрос о целесообразности увеличения запаса дефицитного сырья S3. Из рис.1 видно, что при увеличении этого вида сырья прямая (3) (отрезок BС) перемещается вверх параллельно самой себе. В точке L ограничение (3) становится неактивным, поэтому объем сырья S3 не следует увеличивать сверх этого предела. Этот предельный уровень определяется путем подстановки координат точки L(0;5) в левую часть ограничения (3). В результате получим
1×0 + 2×5 = 10,
F(L) = 3×0 +4×5 = 20.
Рассмотрим теперь вопрос об уменьшении запаса недефицитного сырья S2 (ограничение 2). Из рис.1 видно, что не изменяя оптимального решения прямую (2) (отрезок КЕ) можно перемещать параллельно самой себе до пересечения с точкой С. Уменьшение запаса сырья S2 до величины 8 (2×3 + 1×2 = 8) никак не повлияет на оптимальность полученного ранее решения.
Результаты проведенного анализа помещены в таблице 2.
Таблица 2
| Сырье | Тип сырья | Максимальное изменение запаса | Максимальное изменение прибыли |
| S1 | дефицитное | 16/3 - 5 = 1/3 | 53/3 - 51/3 = 2/3 |
| S2 | недефицитное | 9 - 8 = 1 | 17 - 17 = 0 |
| S3 | дефицитное | 10 - 7 = 3 | 20 - 17 = 3 |
Для ответа на третий вопрос введем характеристики ценности каждой дополнительной единицы сырья. Обозначим ценность дополнительной единицы i-го вида сырья через Yi, где
Yi ={ максимальное приращение F( ) / максимальное изменение запаса сырья Si}.
) / максимальное изменение запаса сырья Si}.
Тогда Y1 = 2, Y2 = 0, Y3 = 1.
Полученные результаты свидетельствуют о том, что дополнительные вложения в первую очередь следует направлять на закупку сырья S1 и лишь затем - на закупку сырья S3.
При выяснении вопроса относительно величины диапазона изменения того или иного коэффициента целевой функции, в котором не происходит изменения оптимального решения опять обратимся к рис.1. Из него видно, что при небольшом изменении коэффициентов целевой функции с1 и с2 прямая F(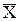 ) =17 вращается вокруг точки С. Таким образом, точка С будет оставаться оптимальной до тех пор пока прямая F(
) =17 вращается вокруг точки С. Таким образом, точка С будет оставаться оптимальной до тех пор пока прямая F(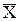 ) не выйдет за пределы, определяемые первым и третьим ограничениями {пока вектор
) не выйдет за пределы, определяемые первым и третьим ограничениями {пока вектор 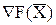 будет находиться между нормалями к первому и третьему ограничениям}.
будет находиться между нормалями к первому и третьему ограничениям}.
Определим сначала диапазон изменения коэффициента с1 при фиксированном коэффициенте с2 (с2 = 4). Тангенсы углов наклона для векторов 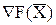 ,
, 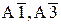 , соответственно равны: tg(
, соответственно равны: tg(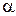 ) = c2/c1, tg(
) = c2/c1, tg(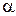 1) = 1, tg (
1) = 1, tg (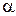 3) = 2.
3) = 2.
Поэтому диапазон изменения коэффициента с1 в целевой функции определится из соотношения 1£ c2/c1 £ 2, т.е. 2 £ c1 £ 4.
Диапазон изменения коэффициента c2 при фиксированном c1 (c1 = 3) определяется аналогично, т. е. 3 £ c2 £ 6.
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 925; Нарушение авторских прав?; Мы поможем в написании вашей работы!