Вычисление определителя и обратной матрицы с помощью метода Гаусса

Метод Гаусса можно использовать для нахождения определителя и обратной матрицы [5, стр.316-317].

Именно, определитель матрицы 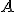равен det .

Обратная матрица 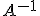находится решением 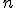систем линейных уравнений методом исключения Гаусса:

, где есть j-тый столбец единичной матрицы , - искомый вектор.

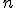Полученные векторы решений - образуют, очевидно, столбцов матрицы 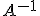, поскольку .

Контрольные вопросы:

1. Дайте определение понятиям «Определитель матрицы», «Обратная матрица».

2. Как ещё в литературе называется определитель?

3. Какими свойствами обладает определитель?

4. Какяя матрица называется транспонированной и как её получить из исходной матрицы?

5. Как разложить определитель по строке или столбцу матрицы?

6. Какая матрица называется треугольной и как привести матрицу к треугольному виду?

7. В чём заключается метод Гаусса при вычислении определителя и обратной матрицы?

Список рекомендуемой литературы:

1. http://e-lib.gasu.ru/eposobia/metody/
2. http://www.exponenta.ru/educat/systemat/slivina/lection/lection2/lection2.asp
3. http://elib.ispu.ru/library/math/sem1/index.html
4. Вычисление матриц Якоби и Гессе
5. Киселёв В.Ю., Пяртли А.С., Калугина Т.Ф. Высшая математика.
6. Боглаев Ю.П. Вычислительная математика и программирование. - М., Высшая школа, 1990, 544 с.
7. Стренг Г. Линейная алгебра и ее приминения / Под ред. Г. И. Марчука. М.: Мир, 1980. 453 c.

Дата добавления: 2013-12-13