Среднее из отсчетов, взятых при двух положениях круга, будет свободно от влияния наклона i горизонтальной оси вращения трубы

Влияние наклона вертикальной оси теодолита на отсчет по горизонтальному кругу

Полагаем, что два первых конструктивных требования к расположению осей теодолита выполнены, т.е. нет с и i, но требование 3 не соблюдено, и вертикальная ось вращения теодолита из—за неточности установки наклонена на некоторый малый угол δ относительно направления отвесной линии (рис. 6.2).

d

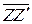— фактическое положение вертикальной оси теодолита;

UU' — ось уровня при горизонтальном круге.

Влияние δ на отсчет в этом случае определится из выражения

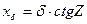(6.6)

При наблюдениях одного и того же предмета при двух положениях круга влияние угла δ на отсчет будет одинаково и с одинаковым знаком. Следовательно, влияние δ, т.е. наклона вертикальной оси теодолита или ее неперпендикулярности к оси уровня, в среднем из двух отсчетов, взятых при двух положениях круга, не исключается.

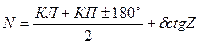(6.7)

Поэтому при наблюдениях углов в триангуляции 1 и 2-го классов во все горизонтальные направления, зенитные расстояния которых отличаются от 90^° на величину более чем на 2^° , вводится поправка за наклон вертикальной оси инструмента.

Наклон δ определяется с помощью отсчетов по концам пузырька накладного уровня (если он имеется) или уровня при горизонтальном круге.

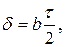
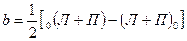, (6.8)

где b – наклон горизонтальной оси трубы в полуделениях уровня;

₀ (Л+П) — сумма отсчетов по левому и правому концам пузырька, когда нуль шкалы уровня находится слева от направления теодолит – визирная цель; (Л+П) ₀ — нуль справа (при другом положении круга).

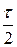- цена полуделения уровня.

Окончательная формула вычисления поправки за наклон вертикальной оси теодолита 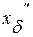имеет вид:

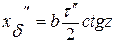(6.9)

В зависимости от теодолита величина b в формуле (6.9) может быть вычислена и по отличающемуся от (6.8) выражению, что указывается в инструкции или в паспорте прибора.

Ошибки нанесения делений на лимб. Способы ослабления их влияния.

Деления на лимбе наносят с помощью автоматической делительной машины. Вследствие действия ряда причин (например, погрешности установки лимба на ось вращения машины, вибрации машины во время ее работы, изменения температуры и т.д.) эти деления наносятся с некоторыми ошибками.

Обозначим через φ и (φ+180^°) фактические положения двух любых диаметрально противоположных штрихов лимба, а через 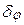и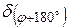- ошибки нанесения этих штрихов. При угловых измерениях отсчеты берутся по диаметрально противоположным штрихам лимба, т.е. всегда используются диаметры лимба, которые характеризуются ошибкой 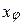. Величину 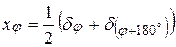называют полной ошибкой диаметра φ.

Полную ошибку 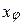диаметра φ представляют в виде суммы систематической x 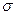и случайной составляющих, т.е.

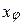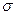= x + (6.10)

Полную 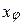и систематическую x 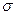ошибки диаметровопределяют из исследований, а случайную - как разность .

Рис. 6.3. Полные 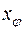и систематические 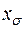длиннопериодические ошибки диаметров лимба теодолита Т05

Ошибки диаметров подразделяются на длиннопериодические (рис. 6.3), т.е. изменяющиеся по всей окружности лимба, и короткопериодические (рис. 6.4),

Рис. 6.4. Короткопериодические (внутриградусные) ошибки диаметров лимба теодолита Т05

Допуск на 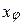у современных теодолитов составляет ±(1¸1.2)".

Ошибки диаметров круга непосредственно влияют на точность угловых измерений. Поэтому каждый лимб тщательно исследуют на его пригодность к высокоточным угловым измерениям.

Известны разные способы определения ошибок диаметра лимба: Пранис-Праневича, Елисеева, Литвинова, Шрейбера, Брунса и т.д. В основе всех способов определения ошибок диаметров лимба лежит последовательное измерение по определенной программе трех углов: b₁ = 36°, b₂ = 45°, b₃ = 60° через интервал Dj = 3°. Обработку выполняют по СНК. Точность определения поправок диаметров характеризуется СКО ±0,1".

Способ ослабления влияния ошибок диаметров лимба на результаты угловых измерений основан на квазипериодическом характере их изменения как в пределах всей окружности (длиннопериодические рис. 6.3), так и внутри градуса (короткопериодические рис. 6.4). При выводе среднего арифметрического из ошибок диаметров, равномерно распределенных по всей окружности через одинаковые интервалы, происходит их значительная компенсация, причем, в тем большей мере, чем меньше эти интервалы.

Поэтому с целью максимальной компенсации ошибок диаметров круга (длинно и короткопериодических) в геодезии при измерении углов и направлений всегда переставляют горизонтальный круг теодолита между приемами на величину:

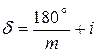или (6.11)

Дата добавления: 2013-12-13