Модуллор ле Корбюзье

Золотое сечение и симметрия

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863...1925) считал золотое сечение одним из проявлений симметрии.

Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.

Размеры человеческого тела на протяжении многих веков являлись основой всех измерений. Мера длины в Египте, Греции, Риме – фут – размер ступни. В России - сажень и локоть – единицы измерения, связанные с ростом человека; пядь – расстояние между большим и указательным пальцами. Дюйм – длина сустава большого пальца. Ладонь – ширина кисти руки. Появившаяся позже десятичная метрическая система имела преимущества перед всеми иными и поэтому получила распространение. Однако она не была связана с размерами человеческого тела. Это обстоятельство побудило выдающегося французского архитектора Ле Корбюзье (1887-1965) для определения предметной среды предложить новую систему «Модуллор». Обвиняя метрическую систему в отсутствии «человечности», избрал для своего метода пропорционирование человека и золотое сечение (рис. 2.56). Главное в этой системе заключалось в том, чтобы найти соответствие основных членений шкалы размерам человека и одновременно совместить принцип модульного расчета с рядами золотого сечения. Ле Корбюзье пришел к выводу, что в основе архитектурных построений должны лежать пропорции человеческой фигуры, связанные по закону золотого ряда.

Свою «золотую линейку» Ле Корбюзье назвал модуллором. По его словам модуллор – это измерение, опирающееся на математику и построенное по принципу «человеческого масштаба».

В первом своем модуллоре Ле Корбюзье принимает средний рост человека за 175см и, исходя из этого размера, строит 2 шкалы золотого сечения. В дальнейшем, стремясь согласовать метрическую систему с измерениями в футах и дюймах, принимается величина роста мужчины в 183 см, т.е. 6 футов (182,88см).

Человек с поднятой рукой дал основные точки, определяющие его положение в пространстве. Нога, солнечное сплетение, голова, кончики пальцев поднятой руки дают интервалы, связанные отношениями золотого сечения: 1130; 698 и 432мм.

Частное от деления меньшего числа ряда на следующее большее – величина постоянная, равная 2/Ѵ5+1.

От средней точки (солнечного сплетения) вниз строится убывающий аддитивный ряд. Начинается ряд с числа 1130 и состоит из составных: 698; 432; 266; 165; 102; 63; 39; 24; 15; 9; 6мм.

В этот ряд сложения внесены некоторые коррективы, чтобы увязать между собою цельночисловое выражение иррационального отношения золотого сечения 2/Ѵ5+1.

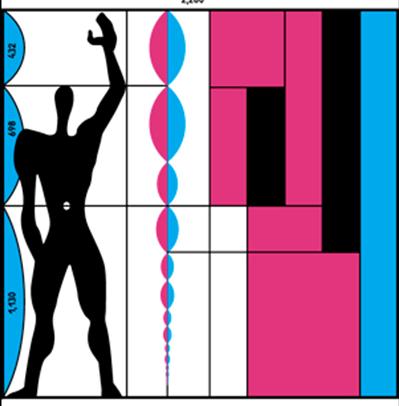
Рис. 2.56 – Модулер

Математическая строгость ряда сложения нарушена в числах 266 и 165. Однако «ошибка» в один миллиметр практического значения не имеет.

Ле Корбюзье получил шкалу золотого сечения, достаточно связанную с основными размерами мужской фигуры, которую он назвал «красной шкалой». Вторая шкала, получившая наименование «синей» была образована путем построения «золотого» ряда, начиная с величины 2260мм, и давала удвоенные величины первой. Синяя шкала имеет следующий вид:

11; 18; 30; 48; 78; 126; 204; 330; 534; 863; 1397; 2260мм и т.д.

Он строит свою пропорциональную систему, как и древнерусские мастера, на двух взаимосвязанных рядах, в которых величины второго ряда равны удвоенным величинам первого.

Две шкалы модуллора Ле Корбюзье дают богатую гамму отношений, позволяющую получить в процессе проектирования гармонически связанные величины.

Набор размеров, округленных до одного сантиметра и составленных на базе красной и синей шкалы Ле Корбюзье, дает возможность получать параметры геометрических форм, связанные между собой по закону золотого сечения или кратности, но в то же самое время близкие габаритам человека.

Красная шкала 6 10 16 27 43 70 113 183…

↘ ↘ ↘ ↘ ↘ ↘ ↘

Синяя шкала 8 13 20 33 53 86 140 226...

Модуллор Ле Корбюзье – это пропорциональный инструмент в основном для индивидуального проектирования. Эстетические задачи пропорционирования в модуллоре недостаточно согласованы с техническими.

Величина чисел пропорциональных рядов, выраженных в миллиметрах или даже округленных до сантиметров, очень осложняет вычисления и согласование строительных деталей. Такая точность для большинства элементов зданий практически не нужна. Более целесообразно пользоваться округленными величинами, дающими большие возможности для унификации элементов.

Здесь возникает вопрос о разумных пределах, в рамках которых, следует строить систему пропорционирования. В свою очередь, пользуясь своим модуллором, Ле Корбюзье строил отдельные здания и целые комплексы сооружений.

Дальнейшее развитие идеи модуллора Ле Корбюзье позволило раскрыть механизм гармонии ритмических взаимосвязей в пропорциях мужского и женского тела, их динамическую дополнительность по отношению друг к другу, что снимает недоверие к золотому сечению на том основании, что пропорции тела женщины не соответствуют золотым.

Ле Корбюзье, разработавший модуллор и осуществивший при его помощи множество прекрасных построек, не считал его универсальным и непогрешимым средством определения пропорций. Иногда ему показывали неудачно, плохо скомпонованные проекты, оправдываясь тем, что это сделано с помощью модуллора. Если модуллор, - отвечал он, - приводит вас к этому безобразию, выкиньте его. Вашим единственным судьей должны быть ваши глаза. Оценивайте все собственными глазами.

Дата добавления: 2013-12-13