Гипотезы, принятые при растяжении и сжатии

Основные понятия и зависимости

Растяжение и сжатие

Лекция № 3

При растяжении (сжатии) прямого бруса в его поперечных сечениях возникает только один внутренний силовой фактор – продольная сила, обозначаемая N_Z или N.

Прямые брусья, работающие на растяжение или сжатие, называют стержнями.

Продольные силы, соответствующие деформации растяжения, условимся считать положительными, а сжатия – отрицательными.

При растяжении продольная сила направлена от сечения, а при сжатии – к сечению.

1. Принцип Сен-Венана: равномерное распределение упругих сил во всех поперечных сечениях. И только в сечениях, расположенных очень близко к местам приложения сил нельзя ожидать равномерного распределения сил упругости. Определение сил упругости в местах, лежащих близко к месту приложения внешних сил, представляет трудную задачу, не входящую в курс сопротивления материалов.

2. Гипотеза Я. Бернулли: сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации.

Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось OZ всех внешних сил, приложенных к оставленной части.

В тех случаях, когда продольные силы в различных поперечных сечениях неодинаковы, закон их изменения по длине бруса удобно представить в виде графика, называемого эпюрой продольных сил N=f(z).

Обозначим полученное удлинение Δ l, его величина будет:

Δ l=l – l_o (мм)

Это приращение длины бруса называется полным или абсолютным удлинением при растяжении, а в случае сжатия бруса оно называется полным или абсолютным укорочением.

Абсолютное удлинение (укорочение), очевидно, зависит от первоначальной длины бруса, поэтому более удобной мерой деформации является удлинение (укорочение), отнесенное к первоначальной длине бруса.

Отношение

называется относительной продольной деформацией или относительным удлинением (укорочением).

Относительное удлинение (укорочение) не имеет размерности и выражается в процентах от первоначальной длины:

Нормальное напряжение, возникающее в поперечном сечении бруса, выразим через продольную силу и площадь сечения:

Единица измерения 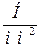или МПа – мегапаскаль.

Нагрузки и деформации, возникающие в брусе, тесно связаны между собой. Эта связь между нагрузкой и деформацией была сформулирована впервые Робертом Гуком в 1678г. Согласно закону Гука деформация пропорциональна нагрузке. Этот закон является одним из основных в теории сопротивления материалов.

(1) - закон Гука

Этот закон справедлив в пределах упругой деформации, но пропорциональность нарушается, когда напряжение переходит за некоторый предел пропорциональности, который устанавливается опытным путем.

Коэффициент Е называется модулем упругости первого рода или модулем продольной упругости (модулем Юнга).

Размерность у Е такая же как и у напряжения σ – мегапаскаль.

При одном и том же напряжении относительная деформация будет меньше у того материала, для которого Е будет больше. Следовательно, модуль упругости характеризует жесткость материала.

Величина модуля упругости устанавливается для материалов экспериментально. Ниже приведены средние значения Е для некоторых материалов при комнатной температуре.

Сталь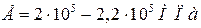

Чугун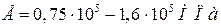

Медь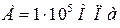

Бронза

Алюминий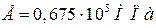

Дерево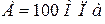

Формулу (1) можно записать в другом виде, если учесть и :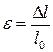

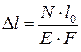(2) – формула Гука

Из формулы (2) следует, что абсолютное удлинение (укорочение), получаемое брусом, прямо пропорционально растягивающей (сжимающей) силе, длине бруса и обратно пропорционально величине - жесткости сечения.

Формулы (1) и (2) являются основными при расчетах на растяжение и сжатие.

Дата добавления: 2013-12-14