ЛЕКЦИЯ №5

МЕХАНИЧЕСКИЕ И ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Колебаниями или колебательными движениями являются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени. Колебания весьма разнообразны по своей физической природе: механические колебания тела, подвешенного на пружине (пружинный маятник), качания маятников, колебания струн, вибрации фундаментов зданий, электромагнитные колебания в колебательном контуре и др.

Колебания называются свободными, если они возникают в системе, не подверженной действию переменных внешних сил, в результате какого-либо однократного начального отклонения этой системы от состояния устойчивого равновесия.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.

Периодом колебания Т называется тот наименьший промежуток времени, по истечении которого повторяются значения всех величин, характеризующих колебательное движение. За это время совершается одно полное колебание.

Частотой периодических колебаний ν называется число полных колебаний, которые совершаются за единицу времени:

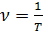(5.1)

Циклической (круговой) частотой периодических колебаний ω называется число полных колебаний, которые совершаются за 2π единиц времени:

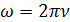(5.2)

Частным случаем периодических колебаний являются гармонические колебания, в которых колеблющаяся физическая величина х изменяется с течением времени по закону:

, (5.3)

где x – значение изменяющейся физической величины в момент времени t, А – амплитуда колебания, 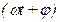– полная фаза колебания, j – начальная фаза, w – собственная круговая частота колебания.

Скорость при гармонических колебаниях описывается уравнением:

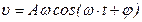. (5.4)

А ускорение - уравнением:

. (5.5)

Амплитудой колебаний A называется величина, равная наибольшему абсолютному значению колеблющейся физической величины х. Фаза колебания 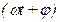определяет значение х в данный момент времени.

Сила, под действием которой точка массой m совершает гармоническое колебание:

(5.6)

Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную смещению сторону.

Кинетическая и потенциальная энергии колеблющейся точки:

(5.7)

Сложив уравнения системы (5.7) получим формулу для полной энергии:

(5.8)

Колебания пружинного маятника.

Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием силы упругости пружины.

Пружинный маятник совершает колебания с циклической частотой:

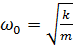(5.9)

И периодом:

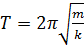(5.10)

где k — жесткость пружины.

Потенциальная энергия пружинного маятника:

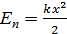(5.10)

Колебания математического маятника

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на невесомой нерастяжимой нити и колеблющейся в вертикальной плоскости под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Период колебаний математического маятника:

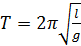(5.12)

Из (5.12) следует, что период малых колебаний математического маятника не зависит от массы маятника и амплитуды его колебаний.

Колебания физического маятника

Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку, не совпадающую с центром масс тела. Период колебаний физического маятника:

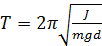(5.13)

где J – момент инерции тела относительно оси вращения, не проходящей через центр масс (центр тяжести), m – масса тела, d – расстояние от центра инерции (центра масс) до оси вращения.

Найти момент инерции J тела относительно оси вращения, не проходящей через центр масс можно по теореме Штейнера:

(5.14)

где J_c – момент инерции относительно оси, параллельной оси вращения и проходящей через центр тяжести. Величина L, равная:

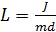(5.15)

называется приведенной длиной физического маятника. Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

Сложение гармонических одинаково направленных колебаний

Если материальная точка участвует одновременно в двух гармонических колебаниях с одинаковой циклической частотой, то происходит сложение гармони­ческих колебаний. В простейшем случае при сложении двух одинаково направленных гармонических колебаний со смещениями x₁ и х₂ одинаковой циклической частоты ω, различающихся своими амплитудами смещений (А₁ и А₂) и начальными фазами (φ₁ и φ₂):

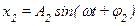, , (5.16)

результирующее гармоническое колебание имеет смещение х=х₁+х₂, происходит в том же направлении и является гармоническим колебанием той же частоты:

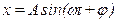(5.17)

где A — амплитуда смещения результирующего колебания, φ – его начальная фаза. А вычисляется по формуле:

(5.18)

Затухающие колебания

Затухающие колебания – это колебания, амплитуда которых уменьшается с течением времени. Затухание свободных гармонических колебаний связано с убылью механической энергии колеблющейся системы за счет действия сил трения и других сил сопротивления.

Амплитуда затухающих колебаний убывает с течением времени по закону:

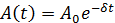(5.19)

где А₀ — начальная амплитуда колебаний в момент времени t=0, которая определяется начальным запасом полной энергии колеблющегося тела, е — основание натуральных логарифмов, δ — коэффициент затухания, зависящий от сил трения и массы колеблющегося тела. Коэффициент затухания характеризует быстроту убывания амплитуды. Коэффициент затухания пропорционален коэффициенту трения r:

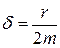(5.20)

Затухающие колебания представляют собой непериодические колебания, так как в них никогда не повторяются значения физических величин, характеризующих такие колебания (например, смещения, скорости и ускорения). Поэтому к затухающим колебаниям неприменимы понятия периода и частоты, введенные для периодических колебаний. Применительно к затухающим колебаниям можно говорить об условном периоде Т: это промежуток времени между двумя последовательными состояниями колеблющейся системы, в которых физические величины, характеризующие колебания, принимают аналогичные значения, изменяясь в одном и том же направлении, убывая или возрастая. Период затухающих колебаний вычисляется по формуле:

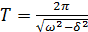(5.21)

где ω — собственная частота свободных незатухающих колебаний, δ — коэффициент затухания.

Вынужденные колебания

Вынужденные колебания это незатухающие колебания системы, которые вызываются действием на нее внешних сил F(t), периодически изменяющихся с те­чением времени. Сила F(t), вызывающая вынужденные колебания, называется возмущающей (вынуждающей) силой.

Если возмущающая сила F(t) изменяется гармонически по закону:

(5.22)

где F₀ — амплитуда возмущающей силы, а ω — ее циклическая частота, то в системе, на которую действует такая сила, могут установиться вынужденные колебания, которые являются также гармоническими, происходят с циклической частотой, равной частоте ω возмущающей силы, и описываются уравнением:

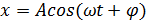(5.23)

Здесь А — амплитуда вынужденных колебаний физической величины (например, смещения), φ — разность фаз между вынужденными колебаниями х и силой F(t). Например, пружинный маятник, который подталкивается вверх периодически, через определенное время начнет колебаться с определенной амплитудой.

Амплитуда А установившихся вынужденных колебаний определяется по формуле:

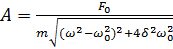(5.24)

где F₀ — амплитуда возмущающей силы, m — масса колеблющейся системы, ω — циклическая частота свободных незатухающих колебаний системы, ω₀ — циклическая частота внешней силы, δ — коэффициент затухания. При постоянных F₀, m и δ амплитуда вынужденных колебаний зависит от соотношения частот вы­нуждающей силы (ω₀) и свободных незатухающих колебаний (ω).

Если колебательная система совершает незатухающие колебания за счет действия источника энергии, не обладающего колебательными свойствами, то такие колебания называются автоколебаниями.

МЕХАНИЧЕСКИЕ (УПРУГИЕ) ВОЛНЫ.

Среда называется упругой, если между ее частицами существуют силы взаимодействия, препятствующие какой-либо деформации этой среды.

Волнами называются всякие возмущения состояния вещества или поля, распространяющиеся в пространстве с течением времени. Например, звуковые волны в газах или жидкостях представляют собой колебания давления, распространяющиеся в этих средах.

Упругими волнами называются механические возмущения (деформации), которые распространяются в упругой среде. Тела, вызывающие эти возмущения в среде, называются источниками волн (колеблющиеся камертоны, струны музыкальных инструментов и т. д.). Упругие волны называются звуковыми или акустическими, если в упругой среде распространяются слабые возмущения, т. е. соответствующие им механические деформации среды имеют малые амплитуды

Волновая поверхность (иначе — фронт волны) - это геометрическое место точек среды, колеблющихся в одинаковых фазах. На волновой поверхности фазы колебаний различных точек в рассматриваемый момент времени имеют одно и то же значение.

Лучом называется линия, касательная к которой в каждой точке совпадает с направлением распространения волны. В однородной изотропной среде луч является прямой, перпендикулярной к фронту волны, и совпадает с направлением переноса энергии волны.

В плоской волне волновыми поверхностями являются плоскости, перпендикулярные к направлению распространения волны. Лучами являются параллельные прямые, совпадающие с направлением скорости распространения волны. Такие волны могут быть получены на поверхности воды с помощью колебаний плоского стержня.

В сферической волне волновые поверхности являются сферами. Такие волны возникают, если источник волн является точечным. Лучи в сферической волне направлены вдоль радиусов сфер от центра, где расположен источник волны (рис. 5.1).

Отличие упругих волн в среде от любого другого упорядоченного движения ее частиц состоит в том, что распространение волн не связано с переносом вещества среды из одного места в другое на большие расстояния.

Поперечные и продольные волны

Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны.

Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.

В газах и жидкостях, которые не обладают упругостью формы, распространение поперечных волн невозможно. В твердых телах возможно распространение как продольных, так и поперечных волн, связанных с наличием упругости формы (например, волны, распространяю­щиеся вдоль струн музыкальных инструментов).

Скорость распространения волн

Скорость распространения волны (фазовая скорость) – это физическая величина, численно равная расстоянию, которое за единицу времени проходит любая точка волновой поверхности. Вектор скорости направлен по нормали к волновой поверхности в сторону распространения волны и в однородной изотропной среде совпадает с направлением луча.

Скорость распространения упругих звуковых волн в газах зависит от термодинамической температуры газа. Для идеальных газов скорость звука:

(5.25)

где R — универсальная газовая постоянная, Т — термодинамическая температура, M — молярная масса, γ — постоянная для данного газа величина, зависящая от строения молекулы газа.

Скорость упругих волн в жидкостях и продольных волн в твердых телах превышает скорость звука в газах и зависит от сжимаемости (упругости) и плотности среды:

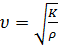(5.26)

где К — модуль объемной упругости, ρ — плотность среды.

Длина волны λ – это расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе, т. е. со сдвигом фаз Δφ=2π. Иначе, длиной волны называется расстояние, на которое распространяется фронт волны за время Т, равное периоду колебаний в источнике волны.

Длина волны связана с частотой колебаний источника волн следующим соотношением:

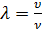(5.27)

где υ — скорость распространения волн, ν — частота колебаний в источнике. Частота колебаний зависит только от свойств источника волн. От свойств среды зависит скорость распространения волн и, вследствие этого, длина волны.

Уравнение плоской волны

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОX:

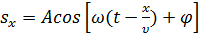(5.28)

Величина:

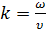(5.29)

называется волновым числом. Оно показывает, сколько длин волн укладывается на расстоянии, равном 2π единиц длины

Уравнение сферической волны:

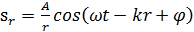(5.30)

Энергия и интенсивность волны.

Колеблющийся источник волн обладает энергией. В процессе распространения волны каждая частица среды, до которой доходит волна, также колеблется и имеет энергию. В некотором объеме V упругой среды, в которой распространяется волна с амплитудой А и циклической частотой ω, имеется средняя энергия 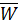, равная:

(5.31)

где m — масса выделенного объема среды.

Интенсивностью волны J называется величина, равная энергии, которую в среднем переносит волна за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны:

(5.32)

где υ — скорость распространения волны, ρ – плотность среды.

Дата добавления: 2013-12-14