ЛЕКЦИЯ №7. В квантовой механике изучаются закономерности явлений, происходящих в микромире — в пределах расстояний порядка 10-15— 10-10 м

КВАНТОВАЯ ФИЗИКА. ФИЗИКА АТОМА.

Спектр атома водорода.

В квантовой механике изучаются закономерности явлений, происходящих в микромире — в пределах расстояний порядка 10^-15— 10^-10 м. Объектами изучения квантовой механики являются атомы, молекулы, кристаллы, а также атомные ядра и элементарные частицы. Спектр излучения атома водорода является линейчатым. Частоты ν_тп линий этого спектра описываются формулой Бальмера — Ридберга:

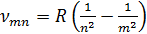, (7.1)

где R=3,293-10¹⁵ с^-1 называется постоянной Ридберга. Целые числа n и m называются главными квантовыми числами, причем m=n+1, n+2 и т. д.

Группа спектральных линий с одинаковым значением n называется серией спектральных линий. Наибольшая частота для каждой серии с главным квантовым числом n соответствует значению m=∞ и называется границей серии или спектральным термом:

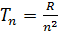, (7.2)

Частота ν_тп линии равна разности термов:

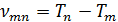, (7.3)

При n=1 получается серия линий, расположенная в далекой ультрафиолетовой части спектра (серия Лаймана):

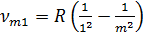, (7.4)

где m=2, 3,...

При n=2 наблюдается серия Бальмера, расположенная в видимой части спектра:

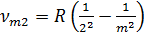, (7.5)

где m=3, 4, 5,...

В инфракрасной части спектра расположены другие серии спектральных линий:

Серия Пашена – n=3, m=4,5,6,…

Серия Брэкета – n=4, m=5,6,7,…

Серия Пфунда – n=5, m=6,7,8,…

Серия Хэмфри – n=6, m=7,8,9,…

В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. Теоретически доказано и экспериментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие переходы, для которых:

1) Изменение орбитального квантового числа Δl удовлетворяет условию:

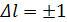
2) Изменение магнитного квантового числа Δm_l удовлетворяет условию:

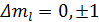
Соотношения неопределенностей

Для волны любой природы представление о том, что она имеет некоторые координаты, находится в определенном месте пространства, лишено физического смысла. Например, если волна, распространяющаяся по поверхности воды, достигла лодки, то не имеет смысла утверждать, что волна находится только в том месте, где она встретилась с лодкой. Когда частица, обладающая волновыми свойствами, дви­жется вдоль некоторой оси, например оси ОX, ее координата на этой оси может быть определена лишь с точностью до величины Δх, называемой неопределенностью координаты частицы. Неопределенностью импульса частицы называется величина Δр, определяемая соотношением:

(7.6)

Согласно соотношению неопределенностей Гейзенберга:

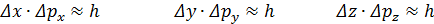, (7.7)

где Δx, Δу и Δz — неопределенности координат частицы по осям ОX, ОY, ОZ; Δр_х, Δр_у, Δр_z — неопределенности проекций импульса частицы по тем же осям, микрочастица не может иметь одновременно определенную координату (x,y,z) и определенную соответствующую проекцию импульса (р_х, р_у, р_z). Соотношение неопределенностей допускает обращение в нуль неопределенности одной из величин, например Δр=0. Это означает, что частица имеет строго определенное значение импульса р (или скорости υ), но тогда Δх=∞. Следовательно, положение частицы на оси ОX (ее координата) становится совершенно неопределенным: частицу можно обнаружить в любом месте на оси ОX в пределах от 0 до ∞.

В связи с тем, что у макроскопических тел волновые свойства не обнаруживаются, соотношение неопределенностей не накладывает для таких тел никаких ограничений на возможность определения их координат и импульсов. Макроскопическое тело, движущееся по оси ОX, может одновременно иметь точные значения координаты и импульса.

Общее уравнение Шредингера.

Уравнение Шредингера является уравнением движения в квантовой механике. Это уравнение является волновым уравнением, т.е. оно учитывает волновые свойства частиц. Оно не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом, что придает ему характер закона природы. Уравнение Шредингера имеет вид:

, (7.8)

где 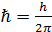, m – масса частицы, Δ – оператор Лапласа, i – мнимая единица, U(x,y,z) – потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y,z,t) – искомая волновая функция частицы. Уравнение (7.8) справедливо для любой частицы, движущейся со скоростью υ<<c. Оно дополняется условиями, накладываемыми на волновую функцию:

1. Волновая функция должна быть конечной, однозначной и непрерывной.

2. Производные 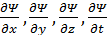должны быть непрерывны

3. Функция 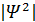должна быть интегрируема.

Для многих физических явлений, происходящих в микромире, можно найти уравнение Шредингера для стационарных состояний – состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором движется частица, стационарно, т.е. функция U = U(x,y,z) не зависит явно от времени и имеет смысл потенциальной энергии. В этом случае уравнение Шредингера будет иметь вид:

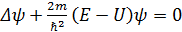(7.9)

Здесь ψ=ψ(x,y,z) – волновая функция, не зависящая от времени, E – полная энергия частицы, постоянная в случае стационарного поля.

Решением уравнения Шредингера для стационарных состояний являются волновые функции – конечные однозначные и непрерывные вместе со своими первыми производными.

Дата добавления: 2013-12-14