
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема. Розвиток теорії планування в реальному часі
|
|
|
|
На практиці нерідко виникають ситуації, коли передумови, покладені в основу алгоритму монотонних частот, не виправдуються. Зокрема, якщо завдання потрібно виконувати не з тими пріоритетами, які призначаються з міркувань монотонності. Базовий алгоритм монотонних частот необхідно поширити й на такі випадки. Один з них - блокування високопріиритетних завдань низькопріиритетними - був описаний у попередньому розділі.
Інший випадок виникає, коли є аперіодичні завдання. У розділі 1.5 ми говорили, що їх можна розглядати як періодичні з еквівалентним періодом, рівним часу між послідовними подіями, що активізують, у найгіршому випадку. Відповідно до алгоритму монотонних частот, якщо період аперіодичного завдання більший, ніж періодичного, то воно повинне виконуватися з більш низьким пріоритетом. Але, якщо аперіодичне завдання активізується перериванням, воно повинне активізуватися, як тільки переривання відбулося, навіть якщо час між перериваннями більший, ніж період періодичного завдання.
1. Інверсія пріоритетів.Термін «інверсія пріоритетів» застосовується до будь-якої ситуації, коли деяке завдання не може продовжити виконання, оскільки блоковано іншим завданням з більш низьким пріоритетом. У випадку алгоритму монотонних частот під пріоритетом розуміється частотно-монотонний пріоритет, призначений завданню винятково на основі довжини її періоду, без обліку відносної важливості. У реальності завданню припустимо призначити пріоритет, відмінний від частотно-монотонного. Коли говорять про інверсію частотно-монотонних пріоритетів, то мають на увазі, що завдання А витиснуте завданням В хоча частотно-монотонний пріоритет завдання В менший, ніж завдання А (тобто період В довший періоду А).
Проілюструємо сказане на прикладі. Нехай є періодичне завдання з періодом 25 мс і завдання, кероване перериваннями, для якого час між послідовними подіями у найгіршому випадку становить 50 мс. Частотно-монотонний пріоритет завдання А вищий, оскільки в нього коротший період, але на практиці більш високий пріоритет краще призначити керованому перериваннями завданню, щоб воно встигало обробляти переривання в міру їхнього надходження. Коли кероване перериваннями завдання витісняє періодичне, виникає ситуація інверсії частотно-монотонних пріоритетів: якби першому завданню призначили звичайний частотно-монотонний пріоритет, витиснення не відбулося б.
Базовий алгоритм частотно-монотонного планування був узагальнений на подібні випадки інверсії пріоритетів за допомогою ефекту блокування низькопріоритетними завданнями, а також витиснення високопріоритетними завданнями, для яких пріоритет не збігається із частотно-монотонним. Оскільки в теорії частотно-монотонного планування передбачається, що пріоритети призначені відповідно до довжин періодів, то другу ситуацію можна трактувати аналогічно першій.
Розглянемо завдання ti з періодом Тi, протягом якого воно використовує С одиниць часу процесора. Якщо ми хочемо узагальнити теореми 1-3, то необхідно явно розглянути кожне завдання ti, щоб визначити, чи встигає вона завершитися до свого першого терміну. Для будь-якого завдання потрібно взяти до уваги чотири фактори:
– час витиснення більш пріоритетними завданнями з періодами меншими, чим в ti. Такі завдання здатні витісняти ti багаторазово. Позначимо множину таких завдань Нn і припустимо, що вона складається з j завдань. Нехай Сj – процесорний час, який споживається завданням j, а Тj – період цього завдання, причому Тj < Тi. Коефіцієнт використання процесора завданням j з множини Нn дорівнює Сj / Тj;
– час виконання завдання ti. Завдання ti виконується один раз протягом свого періоду Тi і споживають Сi одиниць часу процесора;
– витиснення більш пріоритетними завданнями з більшими періодами. Це завдання, пріоритети яких відмінні від частотно-монотонних. Вони можуть витісняти ti тільки один раз, тому що їхні періоди довші, ніж в ti. Назвемо множину таких завдань Н 1 і припустимо, що воно складається з k завдань. Нехай час, використання k- ого завданням із цієї множини, дорівнює Сk. Коефіцієнт використання ЦП для k- ого завдання у найгіршому випадку дорівнює Сk / Тi, тому що при цьому завдання k витісняє t і використовує увесь свій час С, на періоді Тi;
– час блокування завданнями з більш низьким пріоритетом (див. попередній розділ). Ці завдання можуть виконуватися тільки один раз, оскільки мають більш довгі періоди. Затримки через блокування потрібно аналізувати окремо для кожного завдання, щоб визначити ситуацію в найгіршому випадку, яка описується протоколом граничного пріоритету. Якщо Вi – час блокування для завдання ti у найгіршому випадку, то коефіцієнт використання ЦП (теж у найгіршому випадку) для періоду Тi становить Вi / Тi.
2.2. Узагальнена теорема про верхню границю коефіцієнта використання ЦП. Оскільки для будь-якого завдання ti фактори 1 і 2 з попереднього розділу вже враховуються теоремами 1-3, то при узагальненні даних теорем треба взяти до уваги тільки фактори 3 і 4. З обліком всіх чотирьох факторів узагальнена теорема про верхню границю коефіцієнта використання формулюється так.
Узагальнена теорема про верхню границю коефіцієнта використання (теорема 4):

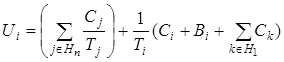
Тут Ui – верхня границя коефіцієнта використання ЦП за період Тi для завдання ti. Перший член в отриманій формулі – сумарне використання за рахунок витиснення високопріоритетними завданнями з періодом меншим, чим в ti. Другий член відповідає використанню процесора завданням ti Третій член враховує час блокування завдання ti у найгіршому випадку, а четвертий – сумарний час витиснення цього завдання більш пріоритетними, але з періодами меншими, чим в ti.
Підставивши значення в наведену формулу, можна визначити значення Ui для даного завдання. Якщо Ui менше верхньої границі для гіршого випадку, то завдання ti задовольняє тимчасовим обмеженням. Важливо розуміти, що перевіряти верхню границю коефіцієнта використання потрібно для кожного завдання: якщо пріоритети призначаються не відповідно до монотонності частот, той факт, що дане завдання задовольняє тимчасовим обмеженням, не припускає того ж відносно більше пріоритетних завдань.
2.3. Узагальнена теорема про час завершення.Як і раніше, якщо узагальнена теорема про верхню границю коефіцієнта використання не дає результату, припустимо застосувати більше точний тест, що дозволяє перевірити, чи зможе завдання завершитися протягом свого періоду. Це узагальнена теорема про час завершення. Вона визначає, чи закінчить завдання ti виконання до кінця свого періоду в умовах витиснення завданнями з більше високими пріоритетами й блокування завданнями з більше низькими пріоритетами. У даній теоремі передбачається гірший випадок, коли всі завдання готові до роботи на початку періоду ti. Графічно узагальнену теорему про час завершення можна представити, намалювавши тимчасову діаграму для всіх завдань аж до моменту завершення періоду Тi завдання ti.
2.4. Планування в реальному часі й проектування.Теорію планування в реальному часі можна застосувати до безлічі паралельних завдань або на етапі проектування, або вже після реалізації всіх завдань. Оскільки під час проектування для часу ЦП існують тільки приблизні оцінки, потрібно бути обережними й при розробці завдань реального часу із твердими тимчасовими обмеженнями покладатися на песимістичну теорему про верхню границю коефіцієнта використання. Ця теорема дає верхню границю 0,69 у найгіршому випадку, хоча теорія планування в реальному часі часто вказує більш високі значення. Якщо верхня границя в найгіршому випадку не може бути досягнута, потрібно вивчити альтернативні рішення. З погляду проектувальника-песиміста, оцінка верхньої границі коефіцієнта вище 0,69 прийнятна за умови, що використання понад 0,69 цілком обумовлено низькопріоритетними завданнями з м'якими тимчасовими обмеженнями або завданнями, які можуть виконуватися не в реальному масштабі часу. Для таких завдань епізодичний пропуск строки виконання не настільки важливий.
Іноді на етапі проектування є певна воля в призначенні пріоритетів завданням. Пріоритети треба по можливості призначати відповідно до алгоритму монотонних частот. Найпростіше застосовувати його до періодичних завдань. Для аперіодичних завдань потрібно оцінити час між подіями в найгіршому випадку й призначити їм частотно-монотонні пріоритети. Завданням, керованим перериваннями, звичайно призначають найвищі пріоритети, тобто перевищуючі частотно-монотонні. Якщо два завдання характеризуються однаковими періодами, а виходить, і частотно-монотонними пріоритетами, то вибір залишається за проектувальником. Більш високий пріоритет рекомендується призначати завданню, що важливіше з погляду додатка.
2.5. Приклад застосування узагальненої теорії планування в реальному часі.Як приклад розглянемо наступний випадок. Є чотири завдання: два періодичні й два аперіодичні. Аперіодичне завдання ta управляється перериваннями й повинне встигнути виконатися протягом 200 мс після переривання, інакше дані будуть загублені. Для іншого аперіодичного завдання час між подіями в найгіршому випадку дорівнює Т2 і воно приймається рівним періоду еквівалентного періодичного завдання. Нижче наведені детальні характеристики завдань, причому час зазначений у мілісекундах, а коефіцієнт використання Ui=Ci/Ti.
Періодичне завдання t 1: С 1 = 20; Т 1 = 100; U 1 = 0,2.
Аперіодичне завдання t2: С 2 = 15; Т 2 = 150; U 2 = 0,1.
Кероване перериваннями завдання ta: Сa = 4; Тa = 200; Ua = 0,02.
Періодичне завдання t 3: C 3 = 30; T 3 = 300; U 3 = 0,1.
Крім того, відомо, що завдання t 1, t 2 і t 3 звертаються до тих самих збережених даних, захищених семафором S. Передбачається, що витрати на контекстне перемикання, один раз на початку й один раз наприкінці виконання завдання, входять у процесорний час, який використовується.
Завданням призначені пріоритети в строгій відповідності з алгоритмом монотонних частот, тобто t 1 має найвищий пріоритет, а за нею ідуть t 2, ta і t 3Але, оскільки для ta час реакції жорстко обмежено, їй привласнений найвищий пріоритет, а вже потім ідуть t 1, t 2 і t 3
Повний коефіцієнт використання ЦП дорівнює 0,42, тобто нижче верхньої границі в найгіршому випадку (вона дорівнює 0,69). Однак необхідно досліджувати кожне завдання окремо, оскільки пріоритети відрізняються від частотно-монотонних.
Спочатку розглянемо кероване перериваннями завдання ta. Оскільки в його найвищий пріоритет, воно отримує процесор за першою вимогою. Коефіцієнт використання тут дорівнює 0,02, так що завдання не буде випробовувати ніяких ускладнень із завершенням у термін.
Далі розберемо завдання t 1, що виконується 20 мс протягом свого періоду Т 1, рівного 100 мс. Для застосування узагальненої теореми про верхню границю коефіцієнта використання треба взяти до уваги чотири фактори:
– час витиснення більш пріоритетними завданнями з періодами меншими, чим Т 1. Таких завдань немає;
– час виконання С 1 завдання t 1 дорівнює 20. Коефіцієнт використання U 1 = 0,2;
– витиснення більш пріоритетними завданнями з більшими періодами. У цю категорію попадає завдання ta. Коефіцієнт використання за рахунок витиснення на періоді Т 1 дорівнює Сa / Т 1 = 4/100 = 0,04;
– час блокування завданнями з більш низьким пріоритетом. Потенційно заблокувати t 1 можуть завдання t 2 і t 3. З огляду на алгоритм граничного пріоритету, ми покладемо, що насправді блокувати t 1 може тільки одне низькопріоритетне завдання. У найгіршому випадку це буде t 3, оскільки вона використовує найбільше процесорного часу – 30 мс. Коефіцієнт використання за рахунок блокування на періоді Т 1 становить B 3/ Т 1 = 30/100 = 0,3.
Коефіцієнт використання в найгіршому випадку дорівнює сумі всіх отриманих коефіцієнтів, тобто 0,04 + 0,2 + 0,3 = 0,54, що менше верхньої границі 0,69. Отже, t 1 задовольняє тимчасовим обмеженням.
Далі розглянемо завдання t 2 яка виконується 15 мс протягом свого періоду Т 2 тривалістю 150 мс. Як і вище, звертаємо увагу на чотири фактори:
– час витиснення більш пріоритетними завданнями з періодами меншими, чим Т 2. Тільки одне завдання t 1 має такий період. Його коефіцієнт використання за рахунок витиснення дорівнює U 1=0,2;
– час виконання С 2 завдання t 2 дорівнює 15. Коефіцієнт використання U 2 =0,1;
– витиснення більш пріоритетними завданнями з більшими періодами. У цю категорію попадає керована перериваннями завдання ta. Коефіцієнт використання за рахунок витиснення на періоді Т 2 дорівнює Сa / Т 2 = 4 / 150 = 0,03. Повний коефіцієнт використання за рахунок витиснення завданнями t 1 і ta становить 0,2 + 0,03 = 0,23;
– час блокування завданнями з більш низьким пріоритетом. Завдання t 3 може блокувати t 2. У найгіршому випадку час блокування складе 30 мс. Коефіцієнт використання за рахунок блокування на періоді Т 2дорівнює B 3 / Т 2 = 30 / 150 = 0,2.
Коефіцієнт використання в найгіршому випадку складе 0,23+0,1+0,2 = 0,53, тобто менше 0,69. Отже, і t 2 задовольняє тимчасовим обмеженням.
Залишилося розглянути завдання t 3 яка виконується 30 мс протягом свого періоду T 3 тривалістю 300 мс. Знову застосуємо узагальнену теорему про верхню границю:
– час витиснення більш пріоритетними завданнями з періодами меншими, чим Т 3. Всі три високопріоритетні завдання попадають у цю категорію, так що повний коефіцієнт використання за рахунок витиснення дорівнює U 1 + U 2 + Ua = 0,2 +0,1 + 0,02 = 0,32;
– час виконання C 3 завдання t 3 дорівнює 30. Коефіцієнт використання U 3 = 0,1;
- витиснення більше пріоритетними завданнями з більшими періодами. Таких завдань немає;
- час блокування завданнями з більше низьким пріоритетом. Таких завдань немає.
Коефіцієнт використання в найгіршому випадку складе 0,32 + 0,1 = 0,42, тобто менше 0,69. Виходить, t 3 також задовольняє тимчасовим обмеженням. Отже, всі чотири завдання встигають виконатися в відведений термін.
3. Аналіз продуктивності за допомогою аналізу послідовності подій
На етапі визначення вимог задається час реакції системи на зовнішні події. Після розбивки на завдання можна почати першу спробу виділення тимчасових (бюджетів) паралельним завданням. Для виявлення завдань, які необхідно виконати при обслуговуванні даної зовнішньої події, використовується аналіз послідовності подій. Щоб показати послідовність подій і завдань, активізованих приходом зовнішньої події, застосовується діаграма послідовності подій, заснована на діаграмі паралельної кооперації.
Варто розглянути зовнішню подію, визначити, яке завдання введення/виведення активізується цією подією і який очікуються ланцюжок внутрішніх подій. Для цього необхідно знати, які завдання активізуються і які завдання введення/виведення генерують відгук системи на зовнішню подію. Далі потрібно оцінити час ЦП, який споживається кожним завданням, і накладні видатки, що складаються з витрат на контекстне перемикання, обробку переривання й міжзадачні комунікації й синхронізацію. Треба проаналізувати також інші завдання, які виконуються в той же період часу. Сумарний час ЦП, який споживається всіма завданнями, які беруть участь у ланцюжку подій, і всіма додатковими завданнями, які виконувалися в той же час, плюс накладні видатки - все разом не повинно перевищити заданий час реакції системи. Якщо ви не знаєте точно часу ЦП, який споживається кожним завданням, приймайте оцінку для гіршого випадку.
Для аналізу повного коефіцієнта використання ЦП необхідно розрахувати час, який споживається кожним завданням на даному інтервалі. Якщо існує кілька шляхів виконання завдання, то потрібно одержати оцінку часу для кожного з них. Потім варто оцінити частоту активізації завдань. Для періодичних завдань це легко. Для асинхронних завдань зручно розглянути середню й максимальну частоту активізації. Помножте час ЦП для кожного завдання на її частоту активізації, просумуйте результати й обрахуйте коефіцієнт використання ЦП.
(Приклад застосування аналізу послідовності подій наведений у розділі 17.5.)
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 685; Нарушение авторских прав?; Мы поможем в написании вашей работы!