Поверхні другого класу

Лекція 8

Нехай A, B ≠ 0; C = 0

Ax²+By²+Dx+Ey+F = 0

Згрупуємо однакові змінні та віднімемо повний квадрат

A(x²+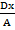)+B(y+Ey)+F = 0

A(x²+2x·+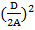-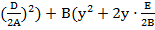+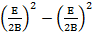)+F = 0

Виділяємо:

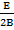A(x+)² - +B(y+)²-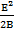+F = 0

Позначаємо:

x₀ = -

y₀ = -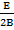

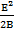∆ = ++F

Маємо:

A(x-x₀)²+B(y-y₀)² = ∆

a) A > 0; B < 0; ∆ = 0

Нехай x₀ = y₀ = 0

Ax² – By² = 0

Y = ±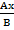

Маємо пару дійсних площин, що витягнуті вздовж осі Z.

b) Якщо A·B > 0 маємо пару уявних площин.

Нехай на площині α є деяка лінія L₁ – напрямна і L₂ – твірна.

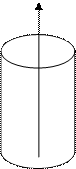
Поверхня з твірною L₂ та напрямною лінією L₁, що одержали рухом L₂ по своєму напрямку L₁ називається циліндричною.

Рівна поверхня, що не містить однієї координати є рівнянням циліндричної поверхні.

· F(x, y) = 0 – поверхня паралельна OZ

· F(x, z) = 0 – поверхня паралельна OY

· F(y, z) = 0 – поверхня паралельна OX

Нехай в рівнянні (10):

1) Ax²+By² = ∆

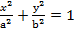
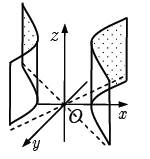Якщо а = b маємо круговий циліндр.

2) Нехай A·B < 0

Маємо Ax²-By² = ∆

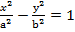
Маємо гіперболічний циліндр.

c) Нехай С = 0

Рівняння має вид Ax²+By²+Fz = ∆

Маэмо параболоїд

1) Ax²+By² = ∆ - Fz

Ax²+By² = - F(z-)

Позначимо:

-F = 2p; = z₀

Маємо:

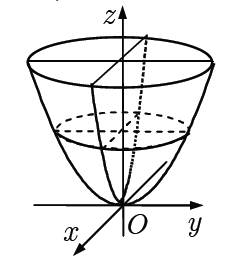Ax²+By² = 2p(z-z₀) (1) – рівняння еліптичного парабалода.

Зробимо перетворення, отримаємо:

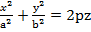(2) – канонічне рівняння, або

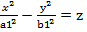(3)

Побудуємо методом перетинів.

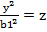, y² = b₁²z

В площині YOZ маємо параболу вздовж вісі OZ. Аналогічно:

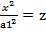, x² = a₁²z – парабола в площині XOY,витягнута вздовж вісі OZ.

, в площині XOY точка О(0,0).

Розглянемо другий випадок

Нехай |B| > 0, A·B < 0, зробимо перетворення:

Ax²-|B|y² = ∆ - Fz

Ax²-|B|y² = - F(z-)

Позначимо:

-F = 2p; = z₀

Маємо:

Ax²-|B|y² = 2p(z-z₀)

Зробимо перетворення, отримаємо:

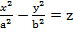(4) – Гіперболічний парабалоїд

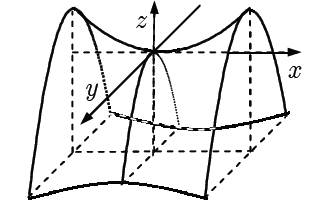Побудуємо методом перетинів.

x = 0

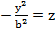, y² = -zb²

В площині YOZ маємо параболу вздовж вісі OZ в від’ємному напрямку.

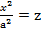’, x² = a²z’ – парабола в площині XOY,витягнута в додатному напрямку вздовж вісі OZ.

z = 0 -> O(0,0)

Дата добавления: 2013-12-14