Методи відсікання

Задача про призначення

Розглянемо транспортну задачу. В якій обсяги в кожному з пунктів i,j і записів б_і і потреб б_j – однакові й дорівнюють одиниці. Тоді з умови /8.15/випливає, що 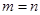. І модель задачі /8.11/=/8.14/ набуває вигляду

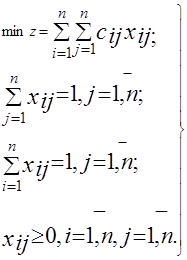/8.16/

Транспортну задачу з постановкою /8.16/ називають задачею про призначення. Як і можна така задача, вона має розв’язок у цілих числах, до того ж обмеження дають смогу змінити х іj набувати тільки значення 0 або 1. Назва задачі пов’язана з такою інтерпритацією її умов.

Є n різних робіт, яким можна доручити різним виконавцям. Призначення виконавці і на роботу j спричинить затрати 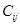. Кожного виконавця потрібно призначити на одну і тільки одну роботу, але так, щоб сумарні затрати не виконання всіх робіт були мінімальні.

Розглянемо задачу про призначення з постійною постановкою – так завну спрощену задачу. Нехай кожен виконавець може виконувати певні, але не всі роботи, і під час розподілу за роботами ураховують тільки те, придатний виконавець до даної роботи чи ні, а затрат не беруть до уваги. Усього є m виконавців і n робіт. Треба розподілити виконавців за роботами так щоб загальна кількість призначень була максимальною і щоб на одну роботу не призначити більше одного виконавця, а одну роботу доручити тільки одному виконавцеві.

Запровадимо матриці , елементи якої можуть набувати одне з двох значень -, коли виконавець придатний до роботи j, i 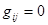в протилежному разі.

Матрицю Q називають матрицею кваліфікацій, її рядки й стовпці- рядками. Клітинками. Що містять одиниці. – допустимими. А нулі – недопустимими.

Таким чином. За умовою всі елементи матриці кваліфікацій поділено на два класи – допустимі і недопустимі клітинки.

Серед практично важливих задач знаходження умовного екстремуму лінійної функції, важливе місце займають задачі з необхідністю цілочисельних всіх чи частини змінних.

Перед тим як формально визначити задачі цілочисельного лінійного програмування розглянемо приклади.

Задачі про призначення. Маємо n видів різних робіт і n робітників для їх виконання. Припускаючи, що кожний кандидат назначається на один і тільки один вид робіт. Позначимо c_ij дохід, який отримується при призначенні і-го кандидата на j-й вид роботи. Необхідно розпреділити кандидатів на роботу так, щоб сумарний дохід від зроблених призначеннях був максимальний.

Нехай

Тоді математичне модель задачі про призначення набуде вигляду:

Максимілізувати

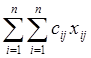
При обмеженнях

j=1,2,…,n; 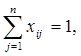i=1,2,…,n (=0, чи =1).

Задача про ранець. В наявності є різноманітні предмети n назв. Турист, збирається в похід, повинен спакувати деякі з них в ранець. Ранець має m обмежень по вазі, об’єму, лінійних розмірів і т.д. пусть а_ij – i-та характеристика (і=1,2,…,m) предмета j-ої назви (j=1,2,…,n); b_i – обмеження по вазі, об’єму, лінійним розмірам і т.д. нехай x_j – кількість предметів j – ої назви, запланових до загрузки в ранець, а с_j – корисність одного предмета

j –ої назви. Тоді математична підстановка задачі набуває наступного вигляду:

- максимілізувати

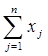
- при обмеженнях

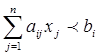і=1,2,…,m;

- ціле, j=1,2,…,n.

Зазначимо, що в початковому формулюванні даної задачі мова йшла не про ранець, а про загрузку бомбардувальників різних типів бойового запасу с ціллю максимілізувати сумарний ефект даної системи бойових операцій.

Задача про вибір типу кораблів (чи інших типів транспортних засобів). Річне пароплавство забезпечує n маршрутів з приблизно однаковою кількістю пасажирів на кожному. Витрати пароплавства для обслуговування кожного з m його пароплавів визначається утримування обслуговуючого персоналу на кожному судні і витратою пального, дохід – кількістю проданих білетів.

Нехай по j – му маршруті перевозиться за сезон b_j⁽¹⁾ чоловік. Перевозку пасажирів по даному маршруті можна виконувати m різними типами кораблів, для кожного і – ого типу судна (і=1,2,…m) відомі слідуючі характеристики:

1) а_і⁽¹⁾ – вантажопідйомність (кількість місць);

2) а_і⁽²⁾ – чисельність обслуговуючого персоналу;

3) а_і⁽³⁾ – витрата пального за сезон;

4) с_ij – прибуток за сезон від використання і-го судна по j – му маршруті.

Необхідно вибрати парк кораблів для кожного маршруту, при якому буде максимальний прибуток судноплавства при виконанні обмежень: загальна витрата пального за сезон не може перевищувати b₃ одиниць, а загальна кількість обслуговуючого персоналу – b₂ чоловік.

Тепер приведемо формальне визначення задачі цілочисельного програмування (в стандартній формі): знайти вектор х=(х₁,…х_n), що мінімізує лінійну функцію

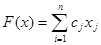
і задовольняючи систему обмежень

і=1,2,…,m;

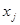, - ціле j=1,2,…,n.

Наведене формулювання відрізняється від звичайної ЗЛП лише умовою цілочисельності, яке накладається на змінні х. цю вимогу приводять до таких специфічних особливостям, що інколи цю задачу відносять до нелінійного програмування.

Якщо цілочисельність накладається лише на деякі змінні, то задача називається задачею частично-цілочисельному програмуванні. Якщо ж змінні можуть приймати лише кінцеву кількість значення (не обов’язково ціле), то говорять, про задачу дискретного програмування.

Здається, цілочисельна задача вирішується простіше, чим звичайна ЗЛП, в силу того, що її допустима величина розв’язків є кінцева множина точок. Але цим не буде змоги скористатися при розв’язанні практичних задач. Наприклад, 64 змінних х, приймають значення лише нуль чи одиниця, дадуть множину точок 2⁶⁴.

Часто при ознайомленні з цілочисельною ЗЛП виникає природне бажання розв’язати цю задачу без врахування цілочисельності х, а потім округлити результат до найблищого цілого. Але такий безпосередній підхід може далеко віднести від оптимального оптимуму.

Приклад 1. В задачі

,

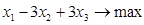
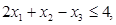
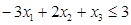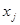, - ціле j=1,2,…,n.

Ров’язком є точка х^*_ц= (2; 2; 5), а без потреби цілочисельна рішення ЗЛП має вигляд х^*= (1/2; 0; 9/2).Звідси, ніякі варіанти округлення рішення допоміжної ЗЛП не дають навіть приблизного рішення початкової задачі цлочисельного лінійного програмування.

Геометрична область допустимих розв’язків звичайної ЗЛП і цілочисельні задачі можна представити так як показано далі.

Але якщо в звичайній ЗЛП перейти від допустимої області D до області D_ц, то розв’язок такої задачі буде цілочисельний.

На жаль, безпосередній перехід від задачі цілочисельного програмування до ЗЛП практично не може бути реалізований, оскільки побудувати область D_ц досить важко. Цю задачу можна вирішити в деякому значенні частково, послідовно врізаючи область D за допомогою так званих відсікаючи площин.

Ідея методів відсікання полягає в слідуючому. Ров’зується ЗЛП, яка отримана з цілочисельною задачі відкиданням умови цілочисельності. Якщо розв’язок допоміжної ЗЛП цілочисельний, то він тоді є розв’язком початкової задачі. Якщо оптимальний розв’язок допоміжної задачі не цілочильний, то тоді до розв’язку цілочисельною задачі додають нове лінійне обмеження; воно задовольняє розв’язок початкової цілочисельною задачі, але не задовольняє отриманому не цілочисельному розв’язку початкової ЗЛП. Вказане доповнення лінійного обмеження оприділяє деяку відсікаючи площину і називається правильним відсіканням. Нові правильні відсікання додають до початкової допоміжної ЗЛП до тих пір, поки на деякому кроці не буде отримане цілочисельний розв’язок допоміжної задачі, який, напевно, буде оптимальним розв’язком початкової задачі цілочисельного лінійного програмування.

Одним із методів відсікання є метод Гоморі.

Розв’язується задача повністю цілочисельним лінійним програмуванням.

………………………………

,

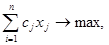
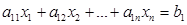
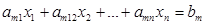де х=(х₁,х₂,…,х_n) – цілочильний вектор.

Поряд з нею розглядається допоміжна ЗЛП

………………………………

,

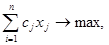
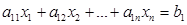
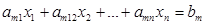отримана з попередньої умови цілочильності вектора х. Задача (3.2) розв’язується симплекс-методом. Нехай на останній ітерації обмеження до цієї задачі прийме вигляд:

………………………………

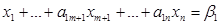
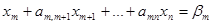
Як відомо, оптимальне рішення задачі (3,2) буде вектор х^*=(β_1,…, β_m;0;…,0). Нехай існує номер і такий, що β_і – неціле (в протилежному випадку цілочисельний вектор х^* буде оптимальним розв’язком і задачі (3.1)).

Позначимо як зазвичай, [z] i {z} відповідно цілу і дробову частину числа z. При цьому, якщо β_і – не ціле число, {β_і} не дорівнює 0.

Відповідно до загальної ідеї метода відсікання перейти до розв’язку нової допоміжної ЗЛП, в якої на ряду з початковими обмеженнями, виконується правильне відсікання. Розглянемо відсікання

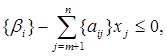
яке відповідає β_і такому, що {β_і} не дорівнює 0. Тоді має місце слідуюче твердження.

Теорема. Додаткове лінійне обмеження (3.3) є правильним відсіканням для задачі цілочильного лінійного програмування (3.1).

Приклад 2. Розв’язати цілочисельного ЗЛП

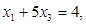
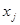, - ціле j=1,2,…,n.

Розв’язуємо допоміжну ЗЛП, яка була отримана із початкової умови цілочисельності 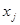, j=1,2,…,n. Розв’язок виконуємо симплекс-таблицею.

№ п/п	сбаз	Базис	А0	-1			θ
А1	А2	А3
	-1	х1 х2					4/5 1/5
	Δ				-2
	-1	х1 х3	1/5		-1 1/5
	Δ			2/5

На останньому кроці обмеження допоміжна ЗЛП має вигляд

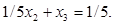
По другому обмеженні будуємо правильне відсікання, яке оприділяється співвідношенням (3.3), а саме:

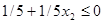чи

Будуємо нову допоміжну ЗЛП, додаючи обмеження Для обмеження «канонізуємо», використовуємо додаткову змінну х₄. отримаємо задачу.

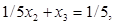
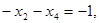
Так як останнє в компоненті вектора вільних членів є від’ємною, отриману ЗЛП розв’язуємо подвійним симплекс-методом. Обчислення проводимо у вигляді симплекс-таблиці.

№ п/п	сбаз	Базис	А0	А1	А2	А3	А4
	-1	х1 х3 х4	1/5 -1		-1 1/5 -1
	Δ			2/5
	-1	х1 х3 х2					-1 1/5 -1

В залежності від звичайного симплекс-метода в подвійному ведучою буде стрічка з від’ємним вільним членом, а ведучий стовпчик, який відповідає додатній симплекс-різниці.

Обчислення в подвійному симплекс-методі закінчується після того як в стовпчику вільних членів А₀ не залишається від’ємних елементів.

Таким чином, на першому кроці подвійного симплекс-методу отримано оптимальне цілочисельне рішення х^*=(4;1;0;0) допоміжної ЗЛП, звідси розв’язком цілочисельною задачі буде х^*=(4;1;0).

Відмітимо, що в практичних обчисленнях відповідність цього метода дуже повільна, реалізація приведеного алгоритму з підвищенням розмірності важка.

Дата добавления: 2013-12-14