Тема 3. Линейное программирование

Вопрос 4. 1.3 Модели управления денежными активами

Вопрос 3. Анализ отчета о движении денежных средств

Анализ отчета о движении денежных средств (ОДДС) позволяет существенно углубить и скорректировать выводы относительно ликвидности и платежеспособности организации, ее будущего финансового потенциала, полученные предварительно на основе статичных показателей в ходе традиционного финансового анализа.

Основная цель ОДДС состоит в предоставлении информации об изменениях объема денежных средств и их эквивалентов для характеристики способности организации генерировать денежные средства.

Денежные потоки организации классифицируются в разрезе текущей, инвестиционной и финансовой деятельности. ОДДС показывает движение объема денежных средств с учетом изменений в структуре денежных притоков и оттоков с учетом сальдо остатков на начало и конец периода, что позволяет определить способность организации поддерживать и генерировать чистый денежный поток, т.е. превышение объема денежных притоков над объемом денежных оттоков с учетом сальдо остатков. Сальдо остатков позволяет управлять ликвидностью, платежеспособностью и финансовой устойчивостью организации.

Прямой метод расчета, основанный на анализе движения денежных средств по счетам предприятия:

– позволяет показать основные источники притока и направления оттока денежных средств;

– дает возможность делать оперативные выводы относительно достаточности средств для платежей по текущим обязательствам;

– устанавливает взаимосвязь между реализацией и денежной выручкой за отчетный период.

Прямой метод направлен на получение данных, характеризующих как валовой, так и чистый денежный поток предприятия в отчетном периоде. Он призван отражать весь объем поступления и расходования денежных средств в разрезе отдельных видов хозяйственной деятельности и по предприятию в целом. Различия результатов расчета денежных потоков, полученных прямым и косвенным методом, относятся только к операционной деятельности предприятия. При использовании прямого метода расчета денежных потоков используются непосредственные данные бухгалтерского учета, характеризующие все виды поступлений и расходования денежных средств.

Формула, по которой осуществляется расчет суммы чистого денежного потока по операционной деятельности предприятия (ЧДПо) прямым методом, имеет следующий вид:

ЧДПо = РП + ППо – Зтм – ЗПо.п – ЗПау – НБб – НПв.ф – ПВо,

где РП – сумма денежных средств, полученных от реализации продукции; ППо – сумма прочих поступлений денежных средств в процессе операционной деятельности; Зтм – сумма денежных средств, выплаченных за приобретение товарно-материальных ценностей – сырья, материалов и полуфабр икатов у поставщиков; ЗПо.п – сумма заработной платы, выплаченной оперативному персоналу; ЗПау – сумма заработной платы, выплаченной административно-управленческому персоналу; НПб – сумма налоговых платежей, перечисленная в бюджет; НПв.ф – сумма налоговых платежей, перечисленная во внебюджетные фонды; ПВо – сумма прочих выплат денежных средств в процессе операционной деятельности.

Расчеты суммы чистого денежного потока предприятия по инвестиционной и финансовой деятельности, а также по предприятию в целом осуществляются по тем же алгоритмам, что и при косвенном методе.

В соответствии с принципами международного учета метод расчета денежных потоков предприятие выбирает самостоятельно, однако предпочтительнее выглядит прямой метод, позволяющий получить более полное представление об их объеме и составе.

Чистые денежные потоки от инвестиционной и финансовой деятельности рассчитываются только прямым методом.

Косвенный метод расчета чистого денежного потока, основанный на анализе статей баланса и отчета о финансовых результатах, позволяет показать взаимосвязь между разными видами деятельности предприятия; устанавливает взаимосвязь между чистой прибылью и изменениями в активах предприятия за отчетный период.

Расчет чистого денежного потока предприятия косвенным методом осуществляется по видам хозяйственной деятельности и предприятию в целом.

По операционной деятельности базовым элементом расчета чистого денежного потока предприятия косвенным методом выступает его чистая прибыль, полученная в отчетном периоде. Путем внесения соответствующих корректив чистая прибыль преобразуется затем в показатель чистого денежного потока. П

Формула, по которой осуществляется расчет суммы чистого денежного потока предприятия по операционной деятельности в рассматриваемом периоде, имеет следующий вид:

ЧДПо = ЧП + АОС+ АНА ± ДЗ ± Зтмц ± КЗ ± Р,

где ЧП – сумма чистой прибыли предприятия; АОС – сумма амортизации основных средств; АНА – сумма амортизации нематериальных активов; ДЗ – прирост (снижение) суммы дебиторской задолженности; Зтмц – прирост (снижение) суммы запасов товарно-материальных ценностей, входящих в состав оборотных активов; КЗ – прирост (снижение) суммы кредиторской задолженности; Р – прирост (снижение) суммы резервного и других страховых фондов.

Результаты проведенных расчетов отражаются в следующей табличной форме

Таблица - Отчет о движении денежных средств предприятия, разработанный прямым методом

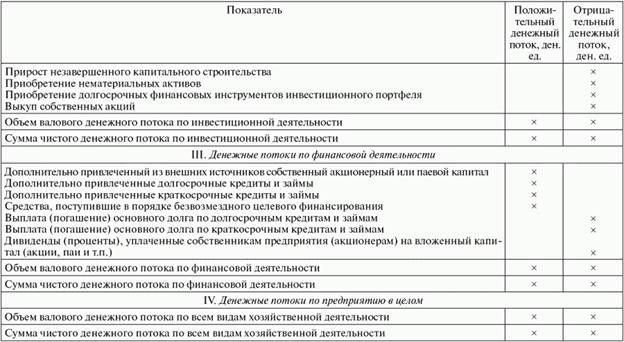
Таблица - Отчет о движении денежных средств предприятия, разработанный косвенным методом

В финансовом менеджменте в процессе управления денежными активами используются: модель Баумоля, модель Миллера–Орра, имитационное моделирование по методу Монте-Карло. Рассмотрим эти модели более подробно.

а) Модель Баумоля. Согласно условиям этой модели, предполагается, что организация начинает работать, имея максимальный и целесообразный для нее уровень денежных средств, и затем постоянно расходует их в течение некоторого периода времени. Все поступающие средства от реализации товаров и услуг организация вкладывает в краткосрочные ценные бумаги. Как только запас денежных средств истощается, т.е. становится равным нулю или достигает некоторого заданного уровня безопасности, организация продает часть ценных бумаг и тем самым пополняет запас денежных средств до первоначальной величины.

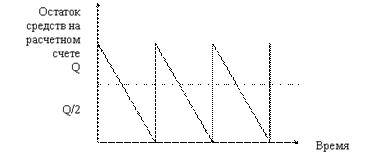
Рисунок 1.1 - График изменения остатка средств на расчетном счете

Сумма пополнения (Q) вычисляется по формуле:

Q = √ (2 * V * с) / r, (1.)

где V – прогнозируемая потребность в денежных средствах в периоде (год, квартал, месяц);

с – расходы по конвертации денежных средств в ценные бумаги;

r – приемлемый и возможный для предприятия процентный доход по краткосрочным финансовым вложениям, например, в государственные ценные бумаги.

Таким образом, средний запас денежных средств составляет Q/2, а общее количество сделок по конвертации ценных бумаг в денежные средства k равно:

k = V / Q (2)

Общие расходы (ОР) по реализации такой политики управления денежными средствами составят:

ОР = с * k + r * (Q / 2) (3)

Первое слагаемое в этой формуле представляет собой прямые расходы, второе – упущенная выгода от хранения средств на расчетном счете вместо того, чтобы инвестировать их в ценные бумаги.

Модель Баумоля проста и в достаточной степени приемлема для организаций, денежные расходы которых стабильны и прогнозируемы. В действительности такое положение бывает относительно редко, остаток средств на расчетном счете изменяется случайным образом, причем возможны значительные колебания.

б) Модель Миллера-Орра.

Модель, разработанная Миллером и Орром, представляет собой компромисс между простотой и реальностью. Она помогает ответить на вопрос: как организации следует управлять своим денежным запасом, если невозможно предсказать каждодневный отток или приток денежных средств? Миллер и Орр используют при построении модели процесс Бернулли – стохастический процесс, в котором поступление и расходование денег от периода к периоду являются независимыми случайными событиями. Остаток средств на счете хаотически меняется до тех пор, пока не достигает верхнего предела.

Рисунок 1.2 - Концепция модели Миллера – Орра

Как только это происходит, организация начинает покупать достаточное количество ценных бумаг с целью вернуть запас денежных средств к некоторому нормальному уровню (точке возврата). Если запас денежных средств достигает нижнего предела, то в этом случае организация продает свои ценные бумаги и таким образом пополняет запас денежных средств до нормального предела.

При решении вопроса о размахе вариации (разность между верхним и нижним пределами) рекомендуется придерживаться следующей политики: если ежедневная изменчивость денежных потоков велика или постоянные затраты, связанные с покупкой и продажей ценных бумаг, высоки, то организации следует увеличить размах вариации, и наоборот. Также рекомендуется уменьшить размах вариации, если есть возможность получения дохода благодаря высокой процентной ставке по ценным бумагам.

Реализация модели осуществляется по следующим этапам.

1. Устанавливается минимальная величина денежных средств (Он), которую целесообразно постоянно иметь на расчетном счете (она определяется экспертным путем исходя из средней организации в оплате счетов, возможных требований банка и др.).

2. По статистическим данным определяется вариация ежедневного поступления средств на расчетный счет (v).

3. Определяются расходы (Pх) по хранению средств на расчетном счете (обычно их принимают в сумме ставки ежедневного дохода по краткосрочным ценным бумагам, циркулирующим на рынке) и расходы (Рт) по взаимной трансформации денежных средств и ценных бумаг (эта величина предполагается постоянной; аналогом такого вида расходов, имеющим место в отечественной практике, являются, например, комиссионные, уплачиваемые в пунктах обмена валюты).

4. Рассчитывают размах вариации остатка денежных средств на расчетном счете (S) по формуле:

S = 3 × √ 3 × PT × V 4 × Px (4)

5. Рассчитывают верхнюю границу денежных средств на расчетном счете (Ов), при превышении которой необходимо часть денежных средств конвертировать в краткосрочные ценные бумаги:

Ов = Он + S (5)

6. Определяют точку возврата (ТВ) – величину остатка денежных средств на расчетном счете, к которой необходимо вернуться в случае, если фактический остаток средств на расчетном счете выходит за границы интервала (Он, Ов):

Тв = Он + (S / 3) (6)

Методы управления денежными средствами предусматривают:

- синхронизацию денежных потоков;

- использование денежных средств в пути;

- ускорение денежных поступлений;

- контроль выплат.

в) Метод Монте-Карло.

Имитационное моделирование по методу Монте-Карло позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию), получить распределение доходности проекта.

Анализ рисков с использованием метода имитационного моделирования Монте-Карло представляет собой «воссоединение» методов анализа чувствительности и анализа сценариев на базе теории вероятностей.

Результатом такого комплексного анализа выступает распределение вероятностей возможных результатов проекта (например, вероятность получения NPV<0).

Первый шаг при применении метода имитации состоит в определении функции распределения каждой переменной, которая оказывает влияние на формирование потока наличности. Как правило, предполагается, что функция распределения является нормальной, и, следовательно, для того, чтобы задать ее, необходимо определить только два момента (математическое ожидание и дисперсию). Как только функция распределения определена, можно применять процедуру Монте-Карло. [28, с.55]

Алгоритм метода имитации Монте-Карло:

Шаг 1. Опираясь на использование статистического пакета, случайным образом выбираем, основываясь на вероятностной функции распределения значение переменной, которая является одним из параметров определения потока наличности.

Шаг 2. Выбранное значение случайной величины наряду со значениями переменных, которые являются экзогенными переменными, используется при подсчете чистой приведенной стоимости проекта.

Шаги 1 и 2 повторяются большое количество раз, например 1000, и полученные 1000 значений чистой приведенной стоимости проекта используются для построения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.

Используя значения математического ожидания и стандартного отклонения, можно вычислить коэффициент вариации чистой приведенной стоимости проекта и затем оценить индивидуальный риск проекта, как и в анализе методом сценариев. Далее необходимо определить минимальное и максимальное значения критической переменной, а для переменной с пошаговым распределением, помимо этих двух, еще и остальные значения, принимаемые ею. Границы варьирования переменной определяются просто исходя из всего спектра возможных значений.

Таким образом, денежные средства являются единственным видом оборотных средств, обладающим абсолютной ликвидностью, то есть немедленной способностью выступать средством платежа по обязательствам организации. Актуальность управления денежными активами определяется тем, что они играют большую роль в производственно-хозяйственной деятельности предприятия - обслуживают все аспекты финансово-экономической деятельности предприятия, обеспечивают финансовое равновесие организации на всех этапах жизненного цикла.

Линейное про­граммирование – раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на уни­версальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного про­граммирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений.

Формы записи задачи линейного программирования:

Общей задачей линейного программирования называют задачу

(1)

при ограничениях

(2)

(3)

(4)

(5)

- произвольные (6)

где - заданные действительные числа; (1) – целевая функция; (1) – (6) –ограничения;

- план задачи.

Наиболее часто используются оптимизационные модели принятия решений. Их общий вид таков:

F(X) → max;

X ϵ A,

где Х — параметр, который менеджер может выбирать (управляющий параметр). Он может иметь различную природу — число, вектор, множество и т.п.

Цель менеджера — максимизировать целевую функцию F(X), вы­брав соответствующий Х. При этом он должен учитывать ограничения X ϵ A на возможные значения управляющего параметра Х — он должен лежать в множестве А. Рассмотрим примеры оптимизационных задач менеджмента.

Среди оптимизационных задач менеджмента наиболее известны задачи линейного программирования, в которых максимизируемая функция F(X) линейная, а ограничения А задаются линейными не­равенствами.

Производственная задача. Цех может производить стулья и сто­лы. На производство стула идет 5 единиц материала, на производство стола — 20 единиц (футов красного дерева). Стул требует 10 человеко- часов, стол — 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула — 45 дол. США, при производстве стола — 80 дол. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?

Обозначим Х1 число изготовленных стульев, Х2 — число столов. Задача оптимизации имеет вид:

45Х1 + 80Х2 → max;

5Х1 + 20Х2 < 400;

10Х1 + 15Х2 < 450;

Х1 > 0; Х2 > 0.

В первой строке выписана целевая функция — прибыль при выпуске Х1 стульев и Х2 столов. Ее требуется максимизировать, выбирая оптимальные значения переменных Х1 и Х2. При этом должны быть выполнены ограничения по материалу (вторая строчка) — истрачено не более 400 футов красного дерева. А также и ограничения по труду (третья строчка) — затрачено не более 450 ч. Кроме того, нельзя забывать, что число столов и число стульев неотрицательны. Если Х1 = 0, то это значит, что стулья не выпускаются. Если же хоть один стул сделан, то Х1 положительно. Но невозможно представить себе отрицательный выпуск — Х1 не может быть отрицательным с экономической точки зрения, хотя с математической точки зрения такого ограничения усмотреть нельзя. В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.

Условия производственной задачи можно изобразить на координатной плоскости. Будем по оси абсцисс откладывать значения Х1, а по оси ординат — значения Х2. Тогда ограничения по материалу и последние две строчки оптимизационной задачи выделяют возможные значения (Х1, Х2) объемов выпуска в виде треугольника (рис. 1).

Рис. 1. Ограничения по материалу

Таким образом, ограничения по материалу изображаются в виде выпуклого многоугольника, в данном случае — треугольника. Этот треугольник получается путем отсечения от первого квадранта примы­кающей к началу координат зоны. Отсечение проводится прямой, соот­ветствующей второй строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось Х1, соответствующую стульям, в точке (80,0). Это означает, что если весь материал пустить на изготовление стульев, то будет изготовлено 80 стульев. Та же прямая пересекает ось Х2, соответствующую столам, в точке (0,20). Это означает, что если весь материал пустить на изготовление столов, то будет изготовлено 20 сто­лов. Для всех точек внутри треугольника выполнено неравенство, что означает — материал останется.

Аналогичным образом можно изобразить и ограничения по труду (рис. 2).

Рис. 2. Ограничения по труду

Ограничения по труду, как и ограничения по материалу, изображаются в виде треугольника, который получается аналогично — путем отсечения от первого квадранта примыкающей к началу координат зоны. Отсечение проводится прямой, соответствующей третьей строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось Х1, соответствующую стульям, в точке (45,0). Это означает, что если все трудовые ресурсы пустить на изготовление стульев, то будет сделано 45 стульев. Та же прямая пересекает ось Х2, соответствующую столам, в точке (0,30). Это означает, что если всех рабочих поставить на изготовление столов, то будет сделано 30 столов. Для всех точек внутри треугольника выполнено неравенство, что означает — часть рабочих будет простаивать.

Мы видим, что очевидного решения нет — для изготовления 80 стульев есть материал, но не хватает рабочих рук, а для производства 30 столов есть рабочая сила, но нет материала, Значит, надо изготавливать и то и другое. Но в каком соотношении?

Чтобы ответить на этот вопрос, надо «совместить» рис. 1 и рис. 2, получив область возможных решений, а затем проследить, какие значения принимает целевая функция на этом множестве (рис. 3).

  Рис. 3. Основная идея линейного программирования

Таким образом, множество возможных значений объемов вы­пуска стульев и столов (Х1, Х2), или, в других терминах, множество А, задающее ограничения на параметр управления в общей оптимизаци­онной задаче, представляет собой пересечение двух треугольников, т.е. выпуклый четырехугольник, показанный на рис. 3. Три его вершины очевидны — это (0,0), (45,0) и (0,20). Четвертая — это пересечение двух прямых — границ треугольников на рис. 1 и рис. 2, т.е. решение сис­темы уравнений

5Х1 + 20Х2 = 400;

10Х1 + 15Х2 = 450.

Из первого уравнения: 5Х1 = 400 - 20 Х2, Х1 = 80 - 4Х2. Подставляем значение X1, выраженное через X2, во второе уравнение:

10(80 - 4Х2) + 15Х2 = 800 - 40Х2 + 15Х2 = 800 - 25Х2 = 450,

следовательно, 25Х2 = 350, Х2 = 14, откуда Х1 = 80 - 4 х 14 = 80 - 56 = 24. Итак, четвертая вершина четырехугольника — это (24, 14).

Надо найти максимум линейной функции на выпуклом многоу­гольнике. (В общем случае линейного программирования — максимум линейной функции на выпуклом многограннике, лежащем в конечно­мерном линейном пространстве.) Основная идея линейного програм­мирования состоит в том, что максимум достигается в вершинах мно­гоугольника. В общем случае — в одной вершине, и это — единственная точка максимума. В частном — в двух, и тогда отрезок, их соединяющий, тоже состоит из точек максимума.

Целевая функция 45Х1 + 80Х2 принимает минимальное значение, равное 0, в вершине (0,0). При увеличении аргументов эта функция увеличивается. В вершине (24, 14) она принимает значение 2200. При этом прямая 45Х1 + 80Х2 = 2200 проходит между прямыми ограничений 5Х1 + 20Х2 = 400 и 10Х1 + 15Х2 = 450, пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24, 14).

Таким образом, оптимальный выпуск таков: 24 стула и 14 столов. При этом используется весь материал и все трудовые ресурсы, а при­быль равна 2200 дол.

Дата добавления: 2013-12-14