
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основи теорії поверхонь
|
|
|
|
Рис. 1.6
Рис. 1.5
Рис. 1.4
Рис. 1.3
Гострий кут, утворений нормаллю до поверхні еліпсоїда і площиною екватора, називається геодезичною широтою і позначається буквою В (рис. 1.3).
Геодезична широта відраховується від площини екватора в межах від 0 до ±90°. Отже, паралель є координатна лінія, у всіх точках якої геодезична широта має одне і теж значення В=const.
Система геодезичних координат В і L представляє собою систему координат, яка дозволяє однозначно визначати положення будь-якої точки на поверхні еліпсоїда. Практичне значення її полягає в тому, що геодезичні координати В і L дуже мало відрізняються від астрономічних координат j і l. Останні, як відомо, визначаються із астрономічних спостережень незалежно від геодезичних вимірювань.
Положення точки Q (Q0 є її проекцією) відносно поверхні еліпсоїда (див. рис. 1.3) визначається геодезичною висотою Н. Відрізок нормалі QQ0 називається геодезичною висотою. Геодезичні висоти відраховуються від поверхні земного еліпсоїда до точок простору, що знаходяться над цією поверхнею.
Оскільки геодезичні координати В, L, Н пов'язані з поверхнею еліпсоїда, то їхще називають еліпсоїдальними координатами.
Система геодезичних координат також може бути задана у вигляді просторових прямокутних координат X, Y, Z, Початок такої системи координат суміщений з центром О еліпсоїда (рис. 1.4), а основною площиною (XОY) служить площина його екватора.
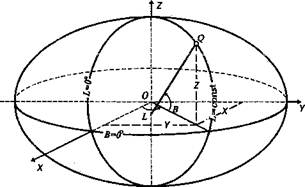
За координатну вісь Х приймається лінія перетину площини екватора еліпсоїда та площини, відповідним чином вибраного, геодезичного початкового меридіана; вісь Y розташована в площині екватора під кутом 90° від початкового меридіана і вісь Z направлена на північ вздовж малої осі ОР еліпсоїда. Зазначимо, що положення початкового геодезичного меридіана відносно початкового астрономічного меридіана залежить від умов орієнтування еліпсоїда в тілі Землі.
Просторові прямокутні прямолінійні координати будь-якої точки X,Y,Z називають ще декартовими координатами цієї точки и просторі.
Положення довільної точки Q2 в просторі по відношенню до точки Q1 (рис. 1.5) можна визначити з допомогою азимута А12 нормальної в точці Q1 площини S, що проходить через точку Q2, зенітної відстані z12 та відрізком D - відстанню між точками Q1 Q2.
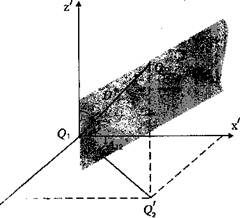
Система координат A,z,D, називається топоцентричною горизонтальною полярною системою. Відома й система топоцентричних горизонтальних координат у вигляді прямолінійних – декартових x´ y´ z´ координат (рис. 1.6).
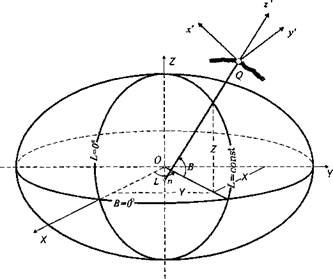
Декартові координати: вісь z´ розташована на продовженні нормалі до поверхні еліпсоїда в точці Q; вісь x´ лежить на перетині площин горизонту та геодезичного меридіана точки Q і направлена на північ; вісь y´ лежить в площині горизонту і доповнює ліву декартову систему координат.
Системи просторових еліпсоїдальних координат B,L,H, просторовихпрямокутних прямолінійних координат X, У, Z, а також плоских прямокутних координат х, у складають геодезичну систему координат, оскільки вони отримуються і використовуються в геодезії.
Геодезична система координат знаходить широке застосування в теоретичних дослідженнях та практичних роботах в геодезії, топографії і картографії, оскільки вона об'єднує дані геодезії, топографічних знімань і картографування всієї поверхні Землі.
Теорію поверхонь слід розглядати із двох боків: внутрішньої геометрії поверхні та зовнішньої геометрії. З позиції першої розглядаються властивості, інваріантні відносно викривлення поверхні, а з другої - властивості, інваріантні відносно групи рухів в просторі. Однією з основних задач сфероїдної геодезії є вивчення внутрішньої геометрії поверхні еліпсоїда обертання.
Сукупність таких властивостей поверхні та фігур на ній, які не змінюютьсяпри викривленні поверхні, називається внутрішньою геометрією поверхні.
Викривленням називається таке перетворення поверхні, при якому довжини всіх ліній, що лежать на цій поверхні, зберігаються.
Накладення однієї поверхні на іншу після викривлення називається розгортанням першої поверхні на другу.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 649; Нарушение авторских прав?; Мы поможем в написании вашей работы!