
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Фур’є для розв’язування задачі про поздовжні коливання стержня
|
|
|
|
Лекція 5 Розв’язування задачі про поздовжні коливання стержня
Контрольні запитання
4.1 Який метод застосовують для розв’язування задач про вільні поперечні коливання нескінченої струни?
4.2 Який метод застосовують для розв’язування задач про вільні поперечні коливання скінченної струни?
4.3 Суть методу Фур’є для розв’язування задач на коливання.
4.4 У чому полягає фізичний зміст розв’язку задачі про поперечні коливання?
4.5
У чому полягає задача про вимушені коливання струни?
Враховуючи, що метод Фур’є застосовують при однорідних крайових умовах, розглянемо задачу про вільні коливання стержня, один кінець якого (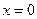 ) жорстко закріплений, а другий (
) жорстко закріплений, а другий (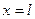 ) вільний. Ця задача має наступну постановку:
) вільний. Ця задача має наступну постановку:

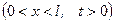 ,
,
П.У. 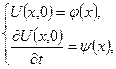 К.У.
К.У.  (5.1)
(5.1)
Припустимо, що функції 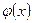 та
та  можна розкласти в ряд Фур’є по синусах кратних дуг на
можна розкласти в ряд Фур’є по синусах кратних дуг на  За методом Фур’є ненульові розв’язки хвильового рівняння, які задовольняють однорідні крайові умови (5.1), шукаємо у вигляді
За методом Фур’є ненульові розв’язки хвильового рівняння, які задовольняють однорідні крайові умови (5.1), шукаємо у вигляді 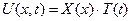 . Знайдемо частинні похідні:
. Знайдемо частинні похідні:

 (5.2)
(5.2)
Після підстановки (5.2) у хвильове рівняння, отримаємо:
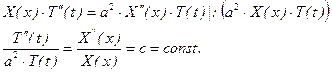 (5.3)
(5.3)
Враховуючи попередні дослідження, відразу розглянемо випадок, який приводить до коливального процесу, оскільки в інших випадках отримуємо тільки нульові розв’язки. Нехай  . Тоді хвильове рівняння розіб’ється на два однорідних диференціальних рівняння другого порядку зі сталими коефіцієнтами відносно функцій
. Тоді хвильове рівняння розіб’ється на два однорідних диференціальних рівняння другого порядку зі сталими коефіцієнтами відносно функцій  та
та 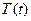 .
.
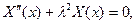 (І)
(І)
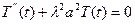 . (ІІ)
. (ІІ)
Розглянемо спочатку перше рівняння і знайдемо функцію 
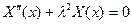 .
.
Характеристичне рівняння 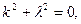
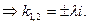
Отже,  (5.4)
(5.4)
де А та В – довільні сталі, які будемо шукати із крайових умов (5.1):
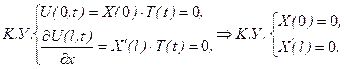
Тут  , щоб уникнути тривіального розв’язку задачі. Знайдемо
, щоб уникнути тривіального розв’язку задачі. Знайдемо 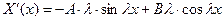 . Тоді крайові умови набувають вигляду:
. Тоді крайові умови набувають вигляду:
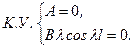 (5.5)
(5.5)
Тут 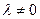 за умовою,
за умовою, 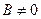 , щоб виключити можливість отримання нульового розв’язку. Тоді
, щоб виключити можливість отримання нульового розв’язку. Тоді  ,
,
 .
.
Звідси визначаємо  , як множину чисел
, як множину чисел 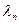 :
:
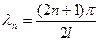 . (5.6)
. (5.6)
Тому 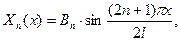 коефіцієнт
коефіцієнт  залишився невизначеним.
залишився невизначеним.
Тепер розглянемо рівняння (ІІ) і знайдемо функцію 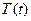
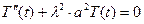 .
.
Характеристичне рівняння 

Тоді загальний розв’язок з урахуванням того, що 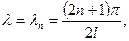 буде таким:
буде таким:
 (5.7)
(5.7)
Запишемо частинний розв’язок поставленої задачі:
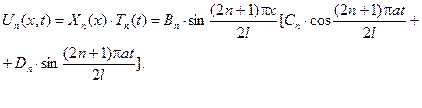 Введемо позначення:
Введемо позначення:  та
та 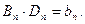
Враховуючи позначення, запишемо загальний р6озв’язок як суму всіх частинних:
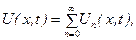 (5.8)
(5.8)
або в розгорнутому вигляді:
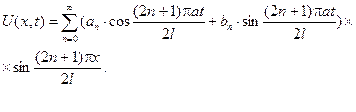 (5.9)
(5.9)
Щоб знайти невідомі коефіцієнти 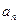 та
та  , скористаємося початковими умовами. Але спочатку знайдемо
, скористаємося початковими умовами. Але спочатку знайдемо 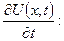
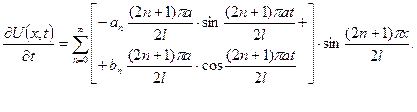
Тепер запишемо початкові умови
 (5.10)
(5.10)
Фактично ми отримали розклади функцій 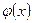 та
та  в ряди Фур’є по синусах в інтервалі
в ряди Фур’є по синусах в інтервалі 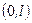 . Тому коефіцієнти розкладів
. Тому коефіцієнти розкладів 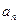 і
і 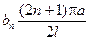 можна визначити за відповідними формулами Фур’є.
можна визначити за відповідними формулами Фур’є.
Таким чином, розв’язок задачі про поздовжні коливання стержня, один кінець якого жорстко закріплений, а другий вільний, має вигляд:
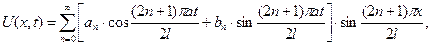
де  , (5.11)
, (5.11)
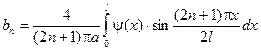 .
.
Приклад 5.1 Розв’язати задачу про поздовжні коливання стержня, один кінець якого жорстко закріплений, а до вільного кінця прикладено силу P, причому в момент t =0 дія сили раптово припиняється.
 Ця задача має наступну постановку:
Ця задача має наступну постановку:

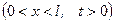 ,
,

Тобто функції  ,
,  Звідси
Звідси 
Щоб побудувати розв’язок у вигляді (5.8) знайдемо коефіцієнти 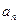 :
:
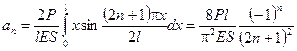 .
.
Тоді розв’язок задачі:
 .
. 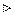
Приклад 5.2 Поставити і розв’язати задачу про поздовжні коливання стержня, один кінець якого жорстко закріплено, а до вільного кінця раптово у момент часу 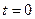 прикладено розтягуючу силу P.
прикладено розтягуючу силу P.
 Ця задача має наступну постановку:
Ця задача має наступну постановку:

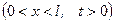 ,
,
П.У. 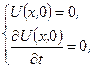 К.У.
К.У. 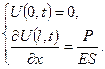
Для того, щоб розв’язати задачу з ненульовими крайовими умовами зробимо заміну 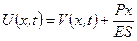 :
:
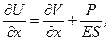
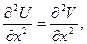

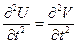 .
.
Отримаємо початкові і крайові умови для функції 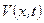 :
:


Постановка задачі для функції 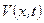 матиме вигляд:
матиме вигляд:
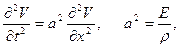
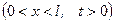 ,
,
П.У.  К.У.
К.У. 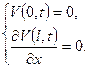
Знайшовши 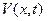 за методом Фур’є, відповідь запишемо у вигляді
за методом Фур’є, відповідь запишемо у вигляді 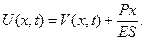
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 1390; Нарушение авторских прав?; Мы поможем в написании вашей работы!