
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Зауваження
|
|
|
|
Розглянемо випадок, коли на кінцях стержня задається ненульова температура. Тоді задача має наступну постановку:
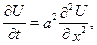
 ,
, 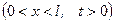 ,
,
П.У.  К.У.
К.У. 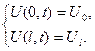 (6.24)
(6.24)
Тут  та
та  – сталі температури відповідно на кінцях х= 0 та x=l.
– сталі температури відповідно на кінцях х= 0 та x=l.
У цій задачі з неоднорідними граничними умовами достатньо зробити підстановку:
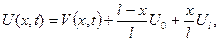 (6.25)
(6.25)
яка зведе її до попередньої задачі відносно функції  Цю процедуру пропонується виконати студентам самостійно.
Цю процедуру пропонується виконати студентам самостійно.
Розглянемо ще одну задачу про поширення тепла у стержні.
2) Знайти розподіл температур в стержні, на одному кінці якого весь час підтримується нульова температура, а другий кінець теплоізольвано при довільній початковій умові.
Поставимо задачу:
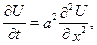
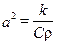 ,
, 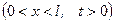 ,
,
П.У. U (x,0)=φ(x), К.У. 
 (6.26)
(6.26)
Зазначимо, що тут не суттєво, який кінець теплоізольовано. Як бачимо, крайові умови однорідні. Розв’яжемо цю задачу за методом Фур’є, згідно якого
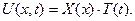 (6.27)
(6.27)
Тоді рівняння теплопровідності:
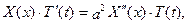
або
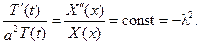
Розглянемо рівняння
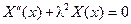 ,
,
розв’язок якого 
Сталі А та В шукаємо із крайових умов:
К.У. 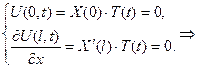
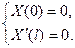
Розпишемо граничні умови:
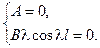
Очевидно, що 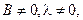 тоді
тоді 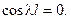
Звідси  ,
, 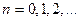
Отже,
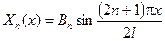 . (6.28)
. (6.28)
Розв’яжемо друге рівняння для функції  , що одержується з рівняння теплопровідності:
, що одержується з рівняння теплопровідності:
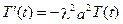 .
.
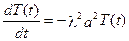
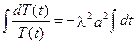 .
.
Розв’язок цього рівняння:
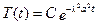 .
.
Враховуючи, що  ,
, 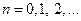 , отримаємо
, отримаємо
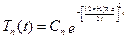 . (6.29)
. (6.29)
Отже, маємо  і розв’язок даної задачі шукаємо у вигляді:
і розв’язок даної задачі шукаємо у вигляді:

Поклавши  , остаточно будемо мати:
, остаточно будемо мати:
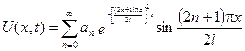 . (6.30)
. (6.30)
Коефіцієнти  визначаються із початкової умови, як у попередній задачі:
визначаються із початкової умови, як у попередній задачі:
 (6.31)
(6.31)
Отже, формули (6.30) і (6.31) дають розв’язок даної задачі.
3) Розв’язати задачу про поширення тепла в стержні, на одному кінці якого стала температура U 0, а другий – теплоізольований.
Поставимо задачу:
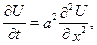
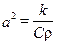 ,
, 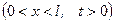 ,
,
П.У. U (x,0)=φ(x), К.У. 
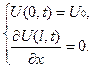 (6.32)
(6.32)
За методом Фур’є крайові умови мають бути нульовими. Тому проведемо заміну


Рівняння теплопровідності:

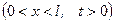 ,
,
К.У.  (6.33)
(6.33)
П.У. 
За методом Фур’є отримаємо
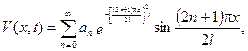 (6.34)
(6.34)
де 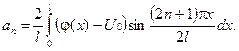
Отже, остаточно маємо: 
Приклад 6.2 Розв’язати задачу про поширення тепла у стержні довжиною l, на кінцях якого весь час підтримується нульова температура, а початковий розподіл температур задається функцією 
 Поставимо задачу:
Поставимо задачу:
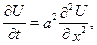
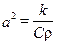 ,
, 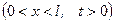 ,
,
П.У. 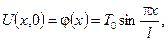 К.У.
К.У. 
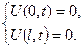
Згідно з методом Фур’є ця задача має розв’язок:
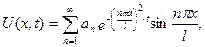
де 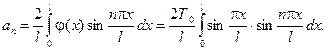
Як відомо, система власних функцій  є ортогональною на проміжку
є ортогональною на проміжку 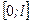 , тобто
, тобто
 коли
коли 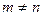 , і не дорівнює нулю, коли
, і не дорівнює нулю, коли  .
.
Таким чином, усі коефіцієнти 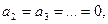 проте коефіцієнт
проте коефіцієнт  Знайдемо його:
Знайдемо його:
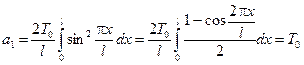
Тоді розв’язок задачі запишемо так
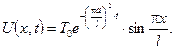
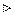
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 554; Нарушение авторских прав?; Мы поможем в написании вашей работы!