Свойства цепи при резонансе напряжений

Способы возбуждения резонанса напряжений

Для возбуждения резонанса напряжений в цепи гармонического тока необходимо обеспечить равенство угловой частоты напряжения источника 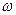и собственной угловой частоты цепи , т.е.

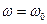(7.8)

Этого равенства можно добиться двумя способами.

1 способ. При неизменных параметрах цепи (L = const, C = const) необходимо изменять угловую частоту напряжения источника питания (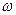= var), приближая ее к собственной частоте цепи:

2 способ. При неизменной угловой частоте напряжения источника питания (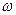= const) необходимо изменять собственную угловую частоту цепи, изменяя ее параметры (L = var, C = var) и обеспечивая приближение собственной частоты контура к частоте напряжения источника питания:

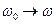
Рассмотрим наиболее характерные свойства цепи в режиме резонанса напряжений.

1. Полное сопротивление цепи в резонансном режиме имеет чисто резистивный характер, равно сопротивлению резистивного элемента и является минимальным.

Действительно, комплексное сопротивление последовательной RLC -цепи:

, откуда полное сопротивление цепи:

.

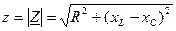В режиме резонанса напряжений , следовательно ,

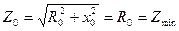. (7.9)

Несмотря на наличие индуктивности L и емкости C, по отношению к источнику питания цепь ведет себя как резистор, т.е. обладает только активным сопротивлением .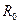

2.Ток в цепи при резонансе напряжений является максимальным и по характеру чисто активным, т.е. не имеет сдвига по фазе по отношению к напряжению, т.е.

; (7.10)

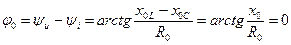. (7.11)

3.Коэффициент мощности цепи равен единице, полная мощность равна активной. Это означает, что ток в цепи при резонансе совершает максимальную полезную работу.

Действительно, при , ,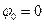

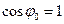(7.12)

или иначе

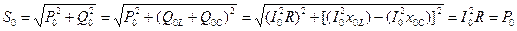(7.13)

гд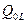е и – реактивные мощности индуктивного и емкостного элементов, характеризующие скорости обратимых преобразований энергии электрического и магнитного полей.

4.В цепи имеют место обратимые преобразования энергии электрического и магнитного полей (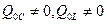), причем интенсивность этих преобразований одинакова: энергия электрического поля конденсатора и энергия магнитного поля катушки преобразуются одна в другую с одинаковой скоростью ().

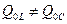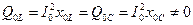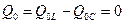; (7.14)

Все колебания энергии (обратимые ее преобразования) имеют место только в пределах внешней цепи, возврата энергии к источнику нет ().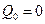

5. Если принять, что при резонансе ток в контуре 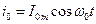, то напряжение на емкости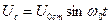. В этом случае мгновенные значения энергии магнитного и электрического полей:

(7.15)

,

.

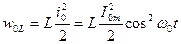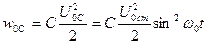Кривые зависимостей w_L и w_C от времени представлены на рис.4.6. В моменты времени t = 0, 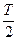,… энергия магнитного поля достигает максимума:

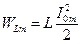, а энергии электрического поля равна нулю; в момент времени 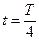, ,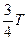…, наоборот, энергия электрического поля достигает максимума

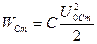, а энергия магнитного поля обращается в нуль.

Рис. 7.2 – Функции энергии на индуктивности и ёмкости от времени

,

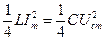
В режиме резонанса максимальные значения энергии магнитного и электрического полей равны:

,

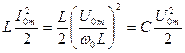где 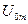– амплитуда напряжения на реактивных элементах при резонансе;

w_L и w_C колеблются с удвоенной частотой около среднего значения

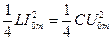
Таким образом, при резонансе напряжений энергия магнитного поля индуктивности преобразуется в энергию электрического поля емкости и наоборот, причем суммарная энергии, запасенная в реактивных элементах цепи, остается постоянной.

(7.16)

Обмен энергией между индуктивностью и емкостью происходит без участия источника энергии, поскольку сдвиг фаз между током и напряжением равен нулю, реактивная мощность, отдаваемая источником, также равна нулю, и обмена энергией между цепью и источником не происходит.

В связи с тем, что в последовательной RLC –цепи имеют место колебания электромагнитной энергии, такая цепь называется последовательным колебательным контуром.

6. Энергия, потребляемая контуром от источника за промежуток времени, равный периоду внешнего гармонического воздействия Т:

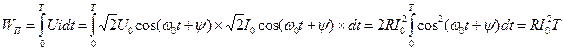. (7.17)

Из этого выражения следует, что энергия, потребляемая контуром от источника, равна энергии, необходимо теряемой в сопротивлении потерь контура R. В идеальном случае, при отсутствии потерь в контуре (т.е. при R = 0), энергия, потребляемая контуром от источника, равна нулю, колебательный процесс в таком контуре будет продолжаться неограниченно долго и при отключении контура от источника.

Таким образом, колебательный процесс в контуре без потерь должен иметь незатухающий характер.

На практике при отключении контура от источника колебаний процесс в нем затухает, так как при каждом цикле колебаний часть электрической энергии, запасенной в контуре, необратимо преобразуется в другие виды энергии. Если контур с потерями подключить к источнику энергии, то амплитуда колебаний в установившемся режиме будет неизменной, так как потери энергии в контуре компенсируются поступлением энергии от источника, и суммарная энергия, связанная с контуром, сохраняет неизменное значение.

Отношение энергии, запасаемой в реактивных элементах контура, и энергии, потребляемой контуром от источника за период Т,

.

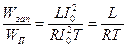Поскольку при резонансе период внешнего гармонического воздействия

, то ,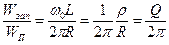

откуда 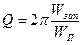(7.18)

Таким образом, добротность колебательного контура характеризует свойство колебательного контура запасать энергию в реактивных элементах, добротность последовательного колебательного контура равна отношению энергии, запасаемой в контуре, к энергии потребляемой контуром за период колебаний, умноженному на 2π.

Выражение (7.18) носит общий характер и может применяться для оценки добротности колебательных систем самых различных типов.

7. Действующие значения напряжений на реактивных элементах равны между собой:

, (7.19)

где 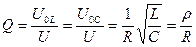(7.20)

Таким образом, добротность контура определяется отношением действующего значения напряжения на реактивном элементе контура при резонансе к действующему значению напряжения на входе контура.

Добротность контура увеличивается с уменьшением резистивного сопротивления контура и с увеличением характеристического сопротивления.

Добротность контура показывает во сколько раз напряжения на реактивных элементах контура при резонансе превышает значение приложенного к контуру напряжения.

Наибольшие достигаемые на практике значения добротности высококачественных колебательных контуров, состоящих из катушек индуктивности и конденсаторов, лежат в пределах 200-500.

Очевидно, что при резонансе напряжений необходимо соблюдать меры электробезопасности при обслуживании радиотехнических систем и электроустановок, а расчет допустимых напряжений конденсаторов и изоляции обмоток катушек необходимо вести из условий обеспечения многократного превышения напряжений на этих элементах по сравнению со значением приложенного к цепи напряжения.

Резонанс напряжений широко используют в электронике, радиотехнике, электросвязи и электротехнике.

2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПОСЛЕДОВАТЕЛЬНОГО

КОЛЕБАТЕЛЬНОГО КОНТУРА

Свойства любой цепи существенно зависят от частоты тока и напряжения, поскольку параметры элементов зависят от частоты.

О свойствах цепи на разных частотах можно судить по частотным и резонансным характеристикам цепи.

Частотные характеристики – это зависимости от частоты параметров контура:

(7.21)

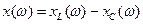
и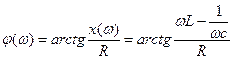

Дата добавления: 2013-12-14