Гистограмма

Всего     Рисунок 7 – Пример контрольного листка  

Конденсаторы

|

Резисторы

Отметки соответствуют числам 1, 2, 3, 4, 5   Наименование Компонента Отметки о количестве Количество Микросхемы

|,

,

Замененные компоненты.

Дата: 23.09.06

Инженер: Иванов А.А.

Отмечайте так |, ||,

Гистограмма –это столбчатый график, построенный по данным, полученным за определенный интервал времени. Данные разбиваются на несколько интервалов, соответствующих столбикам. Высота каждого столбика определяется количеством элементов, попавших в данный интервал. Гистограмма позволяет получить представление о законе распределения случайной величины.

Общий порядок построения гистограмм следующий:

1. Собираются данные контролируемого параметра (x_i) за определенный период (месяц, квартал, год и т.д.). Число данных должно быть не менее 30-50, оптимальное число порядка 100.

2. Определяются наибольшее X _max и наименьшее Х _min значения из всех полученных данных и вычисляется размах R: R = X _max – Х _min. Размах характеризует разброс контролируемой величины, он определяет ширину гистограммы.

3. Полученный диапазон (размах) делится на несколько интервалов. Число интервалов k зависит от общего числа собранных данных n и некоторых других факторов.

Рекомендуется использовать формулу Стерджеса:

k = 1 + 3,322 lg n. (54)

Также можно использовать формулу:

. (55)

4. Далее определяют ширину интервала (величина интервала, интервальная разность):

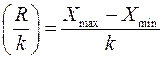. (56)

Все полученные данные распределяют по интервалам. Если какое-то значение попадает на границу, его следует относить к левому по отношению к ней интервалу. Подсчитывается число значений, попавших в каждый интервал m_j, где j -номер интервала.

5. Для каждого интервала подсчитывается относительная частота попадания в него данных

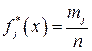. (57)

6. По полученным данным строится гистограмма – столбчатая диаграмма, высота столбиков которой соответствует частоте или относительной частоте попадания данных в каждый из интервалов.

Пример данных для построения гистограммы: Пусть на фрезерном станке изготавливаются пластины, номинальной толщиной 9 мм. Поле допуска на толщину от 6,55 мм до 11,5 мм. Необходимо по значениям толщин группы деталей сделать вывод о состоянии этого станка.

Данные по разбросу деталей приведены в таблице 1

Таблица 1 – Разброс деталей по толщине

Интервал, мм	6,55-7,05	7,05-7,55	7,55-8,05	8,05-8,55	8,55-9,05	9,05-9,55	9,55-10,05	10,05-10,55	10,55-11,05	11,05-11,55	11,55-12,05	12,05-12,55
Количество деталей, попавших в данный интервал, шт.

Гистограмма, построенная по этим данным, приведена на рисунке 8.

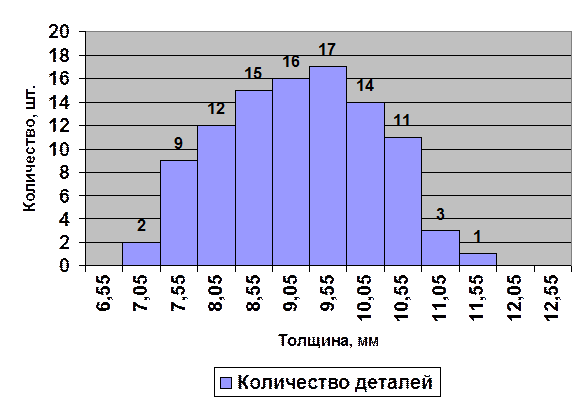
Рисунок 8 – Гистограмма, построенная по данным из примера

Из гистограммы видно, что, несмотря на то, что номинальная толщина 9 мм, больше всего деталей имеют толщину от 9,55 до 10,05 мм. Кроме того, количество деталей с завышенной толщиной больше, чем с заниженной. Это говорит о том, что станок настроен плохо (в сторону больших значений). Фактический разброс не совпадает с полем допуска, т.е. имеет место брак. Ввиду того, что ширина поля допуска и фактический разброс практически одинаковы даже после настройки станка можно ожидать появление брака. Возможно, потребуется заменить станок на более точный, обеспечивающий меньший разброс.

Кроме гистограммы используется полигон (линия, соединяющая середины отрезков на гистограмме) и кумулятивная кривая (КК) (линия, соединяющая правые углы на гистограмме; каждая точка кумулятивной кривой равна сумме всех предыдущих значений).

Примеры кривых распределения, встречающиеся на практике:

а) Поле допуска значительно больше, чем ширина кривой распределения. Брак отсутствует. Используется слишком точный и дорогой станок.

б) Ширина кривой распределения равна ширине поля допуска. Это состояние неустойчиво, стоит чуть сбиться настройкам станка и будет брак.

в) Ширина кривой распределения значительно больше ширины поля допуска. Часть продукции бракованная. Возможно несколько выходов из данной ситуации: приобрести другое оборудование или расширить поле допуска, выбрасывать бракованные детали, сместить центр настройки станка в сторону исправимого брака.

г) Возможно смещение центра настройки станка. Требуется настройка.

д) Если кривая распределения имеет несколько максимумов, то имеет место объединение двух и более распределений, т.е. при построении этой кривой использовались данные двух и более групп деталей, произведенных в разных условиях.

е) Если на кривой нет ярко выраженного максимума, а имеется много значений, близких к максимуму (кривая имеет форму стола). Такая кривая получается в двух случаях: объединены несколько распределений с близкими средними значениями, либо в процессе получения выборки центр настройки оборудования смещался.

ж) Асимметричная кривая распределения имеет место, когда соответствующий технологический параметр имеет односторонне ограничение.

ЛЕКЦИЯ 10. Инструменты контроля качества (часть 2)

____________________________________________________________________

Изучаемые вопросы:

1. Диаграмма разброса.

2. Стратификация.

Дата добавления: 2013-12-13