Dummy – переменные, фиктивные переменные

Включение в модель несущественных параметров.

Спецификация модели

Под спецификацией понимают выбор параметров регрессии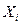. Т.к. на практике исследуется приближенная модель, рассмотрим соотношение между МНК-оценками параметров выбранной и истинной модели.

Рассмотрим два случая:

1) Исключение. В модель не включали существенные параметры. Тогда оценивается модель,

где z - часть существенных параметров.

Мы оцениваем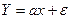

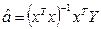
- истинная оценка

Найдем математическое ожидание полученной оценки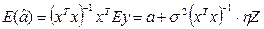

Получаем смещенные оценки, т.е. оценка не такая хорошая, но можно показать, что ее дисперсия будет меньше.

Пусть истинная модель: 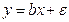, а оценивается модель:

Выписывая оценку коэффициентов b в оцениваемой модели, можно показать, что

оценка несмещенная, но дисперсия 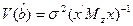, где 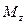– матрица, зависящая от z, т.е. дисперсия оценки увеличивается от включения в модель несущественных параметров.

Следствие: выбирая из двух зол наименьшее, лучше не включать часть существенных параметров, чем включить несущественные.

Как правило, независимые переменные в регрессионных моделях имеют непрерывные области распределения. Однако некоторые переменные могут иметь всего два или дискретное множество значений, например: пол, уровень образования, рейтинг, оценка и т.д.

Например: рассмотрим в качестве зависимой переменной 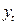– заработная плата, а 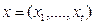- набор объясняющих переменных.

Хотим в модель включить новую бинарную переменную, отвечающую за наличие или отсутствие высшего образования. Тогда необходимо включить в модель новую переменную d (d=1, если t-ый рабочий имеет высшее образование; d=0, если не имеет)

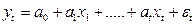
и рассмотреть новую модель

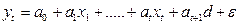
Тогда средняя заработная плата для людей без высшего образования = ; с высшим образованием =

Т.е. коэффициент 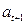интерпретируется как среднее изменение з/п при переходе из одной категории в другую при неизменных остальных параметрах. Т.е. люди с высшим образованием получают на 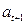рублей больше. Если коэффициент перед незначим, т.е. его р>0,05, то различий в з/п между категориями нет.

Замечание: качественное различие можно формализовать с помощью любой переменной, принимающей два значения, а не обязательно 0 и1. Но тогда интегрируемость коэффициента 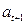усложняется.

Замечание: если включающаяся в модель dummy переменная имеет не два, а несколько значений, то в принципе можно было бы ввести дискретную переменную, принимающую такое же количество значений, но тогда, во-первых, затрудняется интерпретация, во-вторых, подразумевается одинаковое различие между состояниями признака. Поэтому вводят несколько бинарных переменных.

Пример: пусть оценивается стоимость мобильного телефона. В качестве дискретного признака выступает вид телефона:

Вводятся 4 бинарных переменных

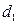
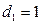, если телефон обычный; 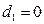, в остальных случаях

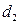
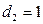, если телефон слим; 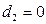, в остальных случаях

, если телефон раскладушка; 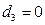, в остальных случаях

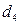
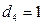, если телефон вертушка; , в остальных случаях

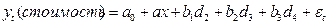
Мы не включили в модель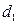, т.к. тогда для любой строки выполнялось бы 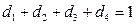, т.е. регрессоры были бы линейно зависимы, т.е. мы не смогли бы получить МНК-оценку параметров, т.к. не смогли бы обратить матрицу.

Интерпретация коэффициентов:

Средняя стоимость телефона слим: 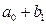, раскладушка: 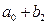, вертушка:

Замечание: если рассматривается ситуация, когда бинарная переменная описывает не все возможные варианты, то в модель включаются все переменные.

Пример: если рассматривается вторичный рынок квартир в Москве, то зависимая переменная – это стоимость 1 кв.м. В качестве одного из факторов используют количество комнат и включают в модель 4 новые переменные следующего вида:

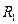
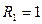, если одна комната; 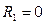, если нет

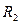
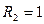, если две комнаты; 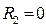, если нет

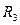
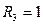, если три комнаты; 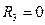, если нет

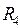
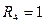, если четыре комнаты; 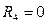, если нет

В модель включаются все 4 переменные, т.к. в базе данных по квартирам присутствуют и многокомнатные квартиры, т.е. больше четырех комнат.

Дата добавления: 2013-12-13