Анализ сезонности во временных рядах

Существует несколько основных методов выделения сезонных и циклических колебаний. К ним относятся:

1.Рассчет сезонной компоненты и построение аддитивной или мультипликативной модели временного ряда. Рассчитывается либо сезонная средняя либо индекс сезонности.

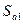
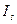
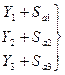аддитивная модель 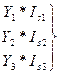коммуникативная модель

2.Анализ сезонности с помощью автокорреляционной функции.

Уt	D^7	D^30
Y1	.
Y2	.
Y3	.
Y4	.
Y5	.
Y6	.
Y7	.
Y8	Y1
Y9	Y2

3.Моделирование с помощью рядов Фурье.

При этом подходе строится зависимость (т.е.регрессионная модель), в которой в качестве характеристик сезонности включается пара sin и cos, характеризующая свои определенные периоды. В данном случае сезонная составляющая представляет собой:

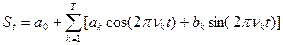
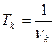- период сезонности.

Например. Если Тк=30 дням, то выявлена ежемесячная сезонность

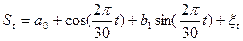
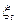- случайная ошибка

В этой модели неизвестными являются параметры, которые находятся с помощью МНК, но для того, чтобы оценки были близки к истинным значениям, необходимо выполнение тех же условий, что и для модели линейной регрессии, а именно

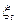~ N – нормальное распределены.

Пример. По выборке о динамике урожайности зерновых культур, в одном из частных хозяйств была построена следующая трендовая модель

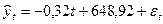
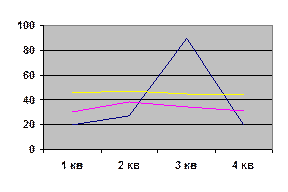
остатки 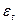оказались не близки к нормальным и их средняя была далеко от 0. Поскольку график остатков явно содержал сезонные составляющие, то для остатков была построена модель сезонных составляющих с помощью ряда Фурье (Microsoft Excel)

После построения модели 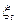оказалось близко к нормальному распределению, а их МО стало близко к 0.

Замечание. Так как большое количество параметров усложняет модель, делает ее сложно применимой и требует большого количества наблюдений, то при анализе сезонности необходимо выбрать основные значимые составляющие, т.е.выбрать только основные периоды сезонности (не больше 4-х периодов). Если вы выбрали 4 периода, то в модель включаются 4 пары sin и cos по одной паре на каждый период.

Пример. На основании данных «Сибнефть» был получен ряд котировок.

03.01.02 – 09.07.03

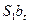
Но проводя анализ остатков было выяснено, что они не близки к нормальным, а их графический (визуальный) анализ позволил получить наличие сезонности. Дальнейший анализ выявил следующую сезонность. Оценки коэффициентов получены в Excel путем построения многомерной регрессии на соответствующие пары sin и cos.

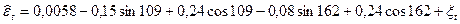
из всех периодов сезонности были выбраны 2 самых значимых (162 и 109)

Т.к.оценивание производится с помощью Excel – Пакет анализ ® Регрессия, то по таблице итогов было видно, что все коэффициенты значимы, R² – высокий, а сами выбранные периоды имели экономический смысл:

1-ый период: 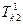=109 дней» 4 месяца» 1/3 года

2-ой период: 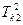=162 дня» полгода.

Замечание 1. Если после построения регрессии на sin и cos из пары синуса и косинуса значима только одна составляющая, то в модель все равно включают пару.

Замечание 2. Основная сложность этого метода состоит в определении значимых периодов. Существует множество различных критериев для определения значимых периодов. Один из самых простых критериев состоит в следующем: выписываются все логически значимые периоды, исходя из сущности…

Т.е.строится множество пар синусов и косинусов (порядка 10-15), а дальше, строя на них регрессию, исходя из значимости коэффициентов, максимизации R² и R² нормированных, устраняют лишние (незначимые) пары синусов и косинусов.

Использование сезонных фиктивных компонент при моделировании сезонных колебаний

При этом подходе строится регрессионная модель, в которую помимо факторов времени включают сезонные фиктивные переменные. Каждому из сезонов соответствует определенное сочетание фиктивных переменных, а 1 из сезонов за базовый.

Например. Если имеются поквартальные данные, то вводятся 3 новые фиктивные переменные. 1-ый квартал считается за базовый.

N	Yt	D2	D3	D4
	Y1
	Y2
	Y3
	Y4
	Y5
	Y6

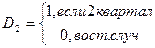
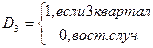
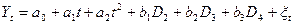
a0,a1,a2,b1,b2,b3 – коэффициенты, полученные МНК

a0+b1 – коэффициент, характеризующий изменение 2-го квартала по сравнению с 1-м.

a0+b2 - коэффициент, характеризующий изменение 3-го квартала по сравнению с 1-м.

a0+b3 - коэффициент, характеризующий изменение 3-го квартала по сравнению с 1-м.

Если коэффициент перед сезонной фиктивной переменной больше 0, то по сравнению с 1-ым кварталом был прирост.

Если же b_i <0, то был спад по сравнению с 1-ым кварталом.

b1,b2,b3 могут иметь разные знаки.

Этот метод удобен для выявления явных простых сезонностей (квартальная, годовая зависимость), но с помощью него не удастся выявить сложную зависимость.

Дата добавления: 2013-12-13