
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Укрепление отбортовкой
|
|
|
|
Наибольший допустимый диаметр некрепленого отверстия в днищах.
Неукрепленным в днище считается отверстие не имеющее усиления в виде отбортованного воротника, приварных штуцеров и накладок.
Наибольший допустимый диаметр неукрепленного отверстия рассчитывается по формулам в зависимости от коэффициента 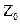 :
:
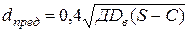 при
при 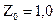
 при
при 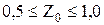
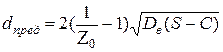 при
при 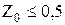 .
.
Коэффициент 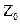 определяется по формуле:
определяется по формуле:

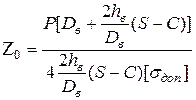 .
.
Если диаметр в днище превышает наибольший допустимый диаметр, то следует или укрепить отверстие или увеличить толщину стенки отверстия.
При укреплении отбортованным воротником (рис.5.9), укрепляющее сечение определяется как
 |

Рис.5.9 Конструктивная схема днища с отбортовкой
Значение минимальной расчётной толщины стенки воротника 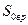 определяется при
определяется при 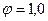 и
и 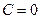 по обычным формулам:
по обычным формулам:

Если отверстие имеет частичное укрепление в виде штуцера или накладки следует вычислить эквивалентный диаметр 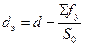 ;
; 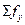 - сумма укрепляющих сечений.
- сумма укрепляющих сечений.
По величине эквивалентного диаметра  определяют значение коэффициента
определяют значение коэффициента 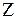 .
.
5.13. Расчёт на прочность сварных тройников.
Тройники, устанавливаемые на трубопроводы, изготавливаются литьём, сваркой и механической обработкой из поковок.
В энергетике широко применяются тройники, сваренные из труб.
Напряжения, возникающие в тройниках, обычно превышают напряжения в неослабленной трубе вследствие удаления части металла для образования отверстия и из-за наличия резкого изменения сечения.
Расчёт сварных тройников на прочность решается с учетом экспериментальных данных.
Коэффициент прочности при расчете сварных тройников определяется по уравнению (рис.5.10)
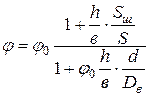
 |
где
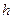 - высота штуцера;
- высота штуцера;
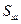 - толщина стенки штуцера.
- толщина стенки штуцера.
Рис.5.10 Конструктивная схема тройника
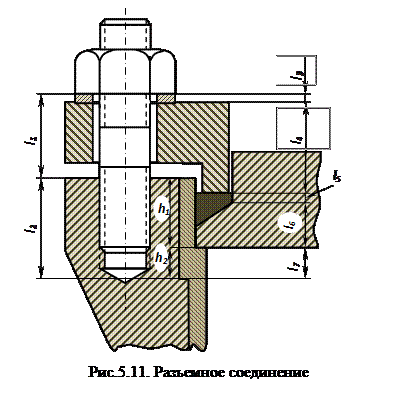
5.14. Расчёт разъёмных соединений
При расчёте разъёмных соединений сосудов рассчитываются усилия начальной затяжки шпилек, усилия в шпильках и на прокладке в условиях эксплуатации, крутящий момент в гайках, а также напряжения в шпильках, которые должны быть меньше предельно допустимых.
Усилия начальной затяжки Рнз шпилек выбираются как наименьшее из трех условий:
Рнз ³ Робж;
Рнз ³ Рпр.г + (1 - x)×Рг;
Рнз ³ Рпр.раб + (1 - x)×Рраб - Qт,
где Робж - усилие, необходимое для сжатия прокладки, H; эта величина определяется по уравнению
Робж = p × Dпс× в × q0;
Dпс - средний диаметр прокладки (рис. 5.11), м;
в - ширина прижимаемой части прокладки, м;
q0 - удельное давление на прокладку при обжатии, Па;
Рпр.г , Рпр.раб - усилие на прокладку, обеспечивающее герметичность при давлении гидроиспытаний и рабочем давлении, Н,
Рпр.г = p × Dпн × в × m × рг,
Рпр.раб = p × Dпн × в × m × р;
Dпн - наружный диаметр прокладки, м;
m - прокладочный коэффициент;
рг, р - расчётное рабочее давление и давление гидроиспытаний, Па,
рг = 1.25 × р;
Рг, Рраб - гидравлическое усилие от давления гидроиспытаний и рабочего давления, Н,
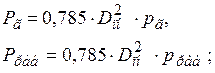
х - коэффициент нагрузки, который определяется по формуле
 ,
,
где lп, lк, lш, lв - коэффициенты податливости прокладки, корпуса, шпильки, шайбы соответственно, м/Н.
Для клиновых, самоуплотняющихся прокладок Рпр = 0,
Коэффициент податливости прокладки, если она находится между фланцами, рассчитывается по формуле
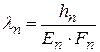 ,
,
где hп - высота прокладки, м;
Еп - модуль упругости материала прокладки, Па;
Fп = p × Dпс× в - площадь прилегания прокладки к фланцам, м2.
Для клиновых и беспрокладочных соединений lп = 0.
 При выборе материала прокладки можно использовать предельные параметры.
При выборе материала прокладки можно использовать предельные параметры.
Коэффициент податливости корпуса lк рассчитывается только тогда, когда между прокладкой и фланцем корпуса устанавливается промтело (например, антикоррозионная рубашка).
Коэффициент податливости шпильки (болта) lш учитывает податливость стержня шпильки (болта) и резьбового соединения и определяется по уравнению
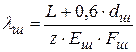 ,
,
где L - свободная длина болта (шпильки) между торцами гайки и головки, прилегающих к фланцам, м;
dш - диаметр стержня шпильки, м;
z - число шпилек;
Fш - площадь поперечного сечения стержня шпильки (болта), м2,
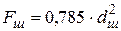 ;
;
Еш - модуль упругости материала шпильки, Па.
Коэффициент податливости шайбы рассчитывается по уравнению
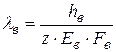 ,
,
где hв - высота шайбы, м; если шайбы установлены с двух сторон, то высота шайбы в расчете берется удвоенной (рис.5.11);
Eв - модуль упругости материала шайбы, Па;
Fв = p×Dвс×вв - площадь поперечного сечения шайбы, м2;
Dвс, вв - средний диаметр и ширина шайбы, м.
Усилие в шпильках (болтах), вызванное температурным перепадом в деталях, соединениях и различием коэффициентов линейного расширения материалов при различных температурах:
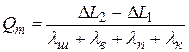 ,
,
где DL2 - температурное удлинение материалов фланца, шайб, прокладки и корпуса, если его необходимо учитывать, м,
DL2 = Shв×aв×tв + SLф×aф×tф + hп×aп×tп;
DL1 - температурное удлинение материалов шпильки (болта), м,
DL1= L ×aш ×tш;
aв, aф, aп, aш - коэффициенты линейного расширения материалов шайб, фланца, прокладки, шпильки, 1/°С;
tф, tв, tп, tш – температура фланцев, шайб, прокладок и шпилек; можно принимать:
tф = tп = tст; tв=0.5×(tок + tст); tш = tок;
где tок - температура окружающей среды, 0С.
Усилия в шпильках (болтах) и на прокладку, Н, в условиях эксплуатации определяются по формулам:
Pш=Pнз + х×Pраб + Qт;
Pп =Pнз - (1 - х)×Pраб + Qт. (6)
На клиновую прокладку действуют осевое и радиальное усилия. По формуле (6) определяется осевое усилие. Радиальная сила R для клиновой прокладки, H, рассчитывается по уравнению
R = Pп / tg(a),
где a - угол прилегания клиновой прокладки, град.
Для клинового уплотнения и беспрокладочного соединения с гибким герметизирующим элементом принимается 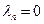 . Если же между крышкой и опорным буртом корпуса устанавливается прокладка, то коэффициент податливости прокладки
. Если же между крышкой и опорным буртом корпуса устанавливается прокладка, то коэффициент податливости прокладки
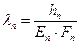
где 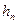 - расчетная высота прокладки, мм;
- расчетная высота прокладки, мм;
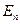 - модуль продольной упругости материала прокладки, кг/мм2;
- модуль продольной упругости материала прокладки, кг/мм2;
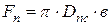 - площадь поперечного сечения прокладки, мм2;
- площадь поперечного сечения прокладки, мм2;
Dпс - средний диаметр прокладки, мм;
в - ширина прокладки, мм;
Коэффициент податливости бурта корпуса 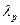 с антикоррозионной рубашкой вычисляют по формуле:
с антикоррозионной рубашкой вычисляют по формуле:
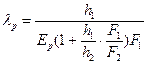
где 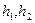 - высота элемента рубашки (рис.5.6), мм;
- высота элемента рубашки (рис.5.6), мм;
 - площадь поперечного сечения элемента выступа рубашки, мм2;
- площадь поперечного сечения элемента выступа рубашки, мм2;
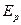 - модуль продольной упругости материала рубашки, кг/мм2.
- модуль продольной упругости материала рубашки, кг/мм2.
Если бурт выполнен на корпусе, не имеющем рубашки, 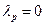 .
.
Коэффициент податливости шпильки 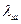 учитывает податливость стержня шпильки резьбового соединения (шпилька - корпус и шпилька - гайка). Величина
учитывает податливость стержня шпильки резьбового соединения (шпилька - корпус и шпилька - гайка). Величина 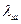 определяется
определяется
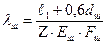
где 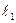 - свободная длина шпильки (между нижним торцом гайки и верхний торцом корпуса, мм;
- свободная длина шпильки (между нижним торцом гайки и верхний торцом корпуса, мм;
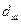 - диаметр стержня шпильки, мм;
- диаметр стержня шпильки, мм;
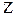 - число шпилек;
- число шпилек;
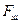 - площадь поперечного сечения стержня шпильки, мм2;
- площадь поперечного сечения стержня шпильки, мм2;
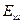 - модуль упругости материала шпильки, кг/мм2;
- модуль упругости материала шпильки, кг/мм2;
Коэффициент податливости втулки (шайбы) вычисляется по формуле:
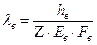
где 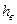 - высота втулки (шайбы), мм,
- высота втулки (шайбы), мм, 
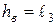 ;
;
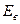 - модуль упругости материала втулки (шайбы), кг/мм2; н/м2
- модуль упругости материала втулки (шайбы), кг/мм2; н/м2
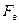 - площадь поперечного сечения втулки (шайбы), мм2;
- площадь поперечного сечения втулки (шайбы), мм2;
Усилия в шпильках, вызванные температурными перепадами в деталях соединения или различием коэффициентов линейного расширения материалов деталей соединения, определяют по формуле:
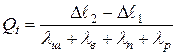 , кг.
, кг.
Пример разбивки соединения по участкам показан на рис.5.6.
Для данного примера
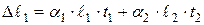
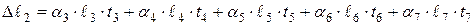
где 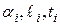 - коэффициент линейного расширения материала, длины участков и средние температуры на участке.
- коэффициент линейного расширения материала, длины участков и средние температуры на участке.
Усилия, необходимые для обжатия прокладки находятся как
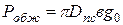 , кг.
, кг.
где 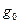 - удельное давление на прокладке при обжатии, кг/мм2;
- удельное давление на прокладке при обжатии, кг/мм2;
Значения 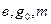 выбираются из табл. 5.3 и 5.4.
выбираются из табл. 5.3 и 5.4.
Усилия на прокладку (кроме клиновой самоуплотняющейся), обеспечивающее герметичность при рабочем давлении и гидроиспытании
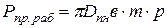 ,
, 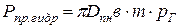 , кг.
, кг.
где 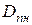 - наружный диаметр прокладки, мм;
- наружный диаметр прокладки, мм;
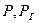 - расчетное рабочее давление и давление гидроиспытаний, кг/мм2;
- расчетное рабочее давление и давление гидроиспытаний, кг/мм2;
Для клиновых самоуплотняющихся прокладок 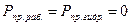 .
.
Таблица 5.3
| Вид прокладки | Условная ширина прокладки 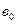 , мм. , мм.
| Эффективная ширина прокладки 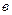 , мм. , мм.
|

|
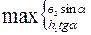
| |

|
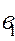
| 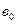 при при 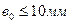 , ,
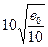 при при 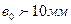
|

| 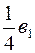
|
Таблица 5.4
| Материал прокладки | Жидкие среды | Воздух, пар, пароводяная смесь | Газы с большой проникающей способностью (водород, гелий, и др.) | |||
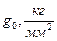
| 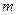
| 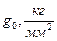
| 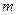
| 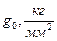
| 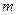
| |
| Паронит | 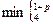
| 1,5 | 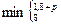
| 2,5 | ||
| Алюминий | 2,0 | 3,5 | ||||
| Медь, никель | 2,5 | 4,5 | ||||
| Мягкая сталь | 3,0 | 5,0 | ||||
| Сталь X18H10T | 3,5 | 6,0 |
Гидростатические усилия от рабочего давления и давления гидроиспытаний определяются как
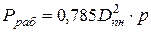 ,
, 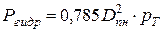 , кг.
, кг.
Усилия начальной затяжки шпилек должно быть выбрано из условий:
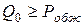 ;
; 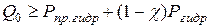 ;
;
Во время действия рабочего давления и температурных перепадов для сохранения герметичности должно быть соблюдено условие
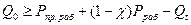 ;
;
Если это условие не соблюдается, то следует выполнить конструктивные изменения соединения или изменить температурные режимы работы. В крайнем случае, допускается увеличение начальной затяжки в соответствии с приведенным условием.
Таким образом, в соответствии с условием начальной затяжки можно найти:
1) усилие на шпильках и на прокладках при затяжке:
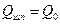 ;
; 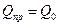
2) усилие на шпильках при гидроиспытании
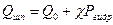
3) усилие на шпильках в рабочих условиях
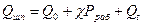
Усилия, действующие на прокладку при гидроиспытании и в рабочих условиях, можно определить в зависимости от типа прокладки:
а) для клиновой прокладки
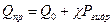
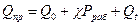
б) для прочих видов прокладок

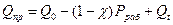
Кроме осевых усилий для клиновых прокладок определяются
радиальные силы
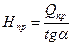 ,
,
При затяжке гаек ключом возникает крутящий момент, Нм, величина которого может быть определена по уравнению
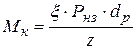 ,
,
где x - коэффициент, учитывающий состояние поверхности резьбы; для чистообработанной резьбы со смазкой x = 0,1; для чистообработанной резьбы без смазки или грубообработанной со смазкой x = 0,13; для грубообработанной резьбы без смазки x = 0,18;
dр - наружный диаметр резьбы шпильки, м.
Напряжения, возникающие в шпильках при эксплуатации, подразделяются на три типа: растяжения, кручения и среза резьбы.
Напряжения растяжения, Па, определяется по формуле
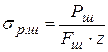 .
.
Напряжение кручения в шпильке, Па,
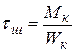 ,
,
где Wк - момент сопротивления сечения стержня шпильки кручению, м3,

Напряжение среза резьбы шпильки, Па, рассчитывается по уравнению
 ,
,
где d1 - внутренний диаметр резьбы, м;
h - высота рабочей части резьбы (резьбового соединения), м.
Исходя из энергетической теории прочности, расчет шпилек разъемного соединения должен удовлетворять следующим условиям:
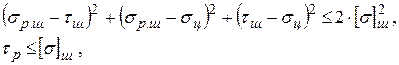
где sц - радиальное напряжение в шпильке, Па, можно принять sц = 0;
[ s ] ш - допустимое напряжение металла шпильки, Па.
Для материала прокладки также должны соблюдаться условия:
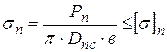 ,
,
где [ s ] п - допустимое напряжение материала прокладки, Па.
5.15. Расчёт на прочность деталей насоса.
В энергоустановках турбомашины находят широкое применение. Например, питательные, конденсатные, дренажные насосы, в водо-водяных и водографитовых реакторах канального типа применяются циркуляционные насосы, для которых необходимо выполнять прочностные расчеты. К основным рассчитываемым узлам и деталям насоса относятся: вал, подшипниковые узлы, уплотнения и узлы корпуса.
При прочностных расчетах насосов определяются: критические скорости вращения вала, при которых появляется повышенная вибрация; критерии жесткости вала, дисбалансировочные нагрузки; удельное давление на подшипниковую опору и др.
 |
1. При работе турбомашин всегда наблюдается некоторая вибрация, вызванная колебанием вращающихся элементов машины. При определенных скоростях вращения появляется повышенная вибрация, при которой частота собственных колебаний совпадает с частотой вынужденных колебаний вала. Этот резонанс можно выразить графически (рис.5.12).
Рис.5.12. Частотная характеристика турбомашины
Для циркуляционных насосов атомных реакторов отношение критического числа оборотов вала к номинальному рабочему должно удовлетворять условию
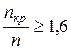
Первую критическую скорость вращения консольного вала при коэффициенте 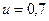 определяют по формуле
определяют по формуле
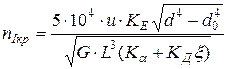 , об/мин.
, об/мин.
где 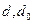 - наружный и внутренний диаметры консольного участка вала, примыкающего к подшипниковой опоре, мм;
- наружный и внутренний диаметры консольного участка вала, примыкающего к подшипниковой опоре, мм;
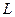 - длина консольного участка вала, мм;
- длина консольного участка вала, мм;
 - приведенный к концу консоли вес консольного участка вала; определяется как
- приведенный к концу консоли вес консольного участка вала; определяется как 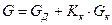 ;
;
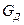 - вес сосредоточенного груза на конце консоли (вес рабочего колеса и его крепления), кг;
- вес сосредоточенного груза на конце консоли (вес рабочего колеса и его крепления), кг;
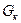 - вес консольного участка вала (без рабочего колеса), кг;
- вес консольного участка вала (без рабочего колеса), кг;
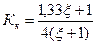 - коэффициент приведения;
- коэффициент приведения;
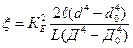 - коэффициент приведения жесткости междуопорного пролета к жесткой консоли;
- коэффициент приведения жесткости междуопорного пролета к жесткой консоли;
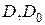 - наружный и внутренний диаметры вала в средней части междуопорного пролета, мм;
- наружный и внутренний диаметры вала в средней части междуопорного пролета, мм;
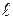 - расстояние между опорами;
- расстояние между опорами;
 - коэффициент, учитывающий изменение модуля упругости на консольном участке вала;
- коэффициент, учитывающий изменение модуля упругости на консольном участке вала;
 |
Е - модуль упругости материала вала на консольном участке при расчетной температуре;
Рис.5.13. Конструктивная характеристика вала турбомашины
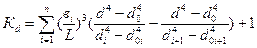 - коэффициент, учитывающий непостоянство диаметра консоли;
- коэффициент, учитывающий непостоянство диаметра консоли;
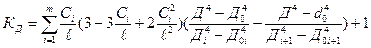 - коэффициент, учитывающий непостоянство диаметра межопорного пролета вала;
- коэффициент, учитывающий непостоянство диаметра межопорного пролета вала;
u - коэффициент, характеризующий влияние массы междуопорного пролета на критическую скорость вала; определяется в зависимости от величины 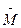 и
и 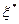 по графику (рис.5.14), где
по графику (рис.5.14), где
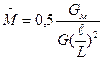
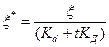
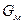 - вес междуопорного пролета, кг;
- вес междуопорного пролета, кг;
t - температура вала, 0С.
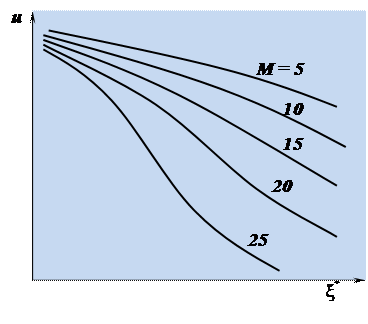 |
Рис.5.14. Зависимость коэффициента влияния массы междуопорного пролета на критическую скорость
Для неконсольного вала и консольного при любой величине коэффициента u
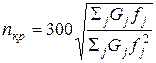 , об/мин.
, об/мин.
где 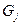 - вес участка вала с насаженными деталями, кг.;
- вес участка вала с насаженными деталями, кг.;
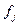 - прогиб (рис.5.15), определяемый путем численного интегрирования дифференциального уравнения
- прогиб (рис.5.15), определяемый путем численного интегрирования дифференциального уравнения
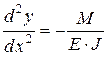 ,
,
где М - изгибающий момент в стыке, кг/мм.;
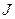 - момент инерции вала, мм4.
- момент инерции вала, мм4.
 |
Рис.5.15. Конструктивная схема определения координат оси вала
2. Для подшипниковых опор насосов определяют удельное давление q, скорость скольжения υ и характеристику q υ.
Для насосов с масляными опорными подшипниками скольжения
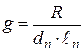 , кг/мм2
, кг/мм2
где R - величина радиальной нагрузки, кг;
dn - диаметр шейки подшипника, мм;
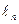 - рабочая длина подшипника, мм.
- рабочая длина подшипника, мм.
Удельное давление на пяте упорного подшипника скольжения с масляным охлаждением определяется по формуле:
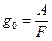 , кг/мм2
, кг/мм2
где А - величина осевой нагрузки;
F - контактирующая площадь вкладышей пяты, мм2.
Скорость скольжения находится как
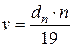 , мм/сек;
, мм/сек;
где n - число оборотов ротора насоса в минуту, об/мин.
Допускаемые значения q, υ и q υ зависят от материалов трущихся пар, параметров системы смазки и охлаждения, конструкции пяты и т.д.
Для подшипников скольжения с трущейся парой является бабит (Б-83 ГОСТ 1320-55) по закаленной стали с принудительной смазкой и охлаждением турбинным маслом.
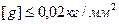 ,
, 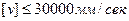 ,
, 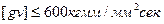
Для конструкции пяты с самоустанавливающимися подрессорными вкладышами с трущейся парой бабит по закаленной стали с принудительной смазкой и охлаждением турбинным маслом
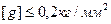 ,
, 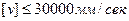 ,
, 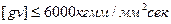
Работоспособность и грузоподъёмность нижнего подшипника определяют из специального гидравлического расчета и проверяют стендовыми испытаниями опытных образцов. Испытания обычно проводят на всем диапазоне рабочих скоростей вращения вала насоса и в режиме многократных пусков и остановок.
5.16. Расчёт перемещений, усилий и напряжений в элементах корпуса
При проведении поверочного расчета приходится определять не только напряжения и усилия, действующие на элементы оборудования, но и величины перемещений и деформаций этих элементов. Поверочный расчет производится после выбора всех основных размеров рассчитываемых элементов, с учетом всех расчетных нагрузок для всех расчетных случаев.
При составлении расчетной схемы узлы конструкции заменяют набором простых элементов (цилиндрических, конических и т.д.). При этом элементы подбирают таким образом, чтобы они по геометрии максимально приближались к натурной конструкции. Например, на рис.5.16 представлена разбивка на элементы фланцевого соединения корпуса сосуда.
Перемещения и усилия, возникающие при действии совокупности нагрузок, вычисляются методом наложения. Деформации же могут быть определены по напряжениям с помощью линейной зависимости между деформациями и напряжениями (по закону Гука).
Взаимодействие элементов заменяют изгибающим моментом, перерезывающей и продольными силами, приложенными по среднему радиусу стыков. В таких расчетных схемах силы трения по контактным поверхностям рассчитываемых деталей не учитываются.
Усилия определяются из решения системы уравнений совместности перемещений
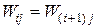 ;
; 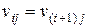
где W - радиальное перемещение для сосудов, мм;
v - угол поворота элемента, рад,;
i, j - номер элемента конструкции и сторона элемента (a, b, c);
n – точка, для которой записывают перемещения.
Знаки перемещений в уравнениях принимают с учетом общей системы координат, принятой в расчетной схеме.
 |
Рис.5.16. Конструктивная схема разбивки узла на элементы
В нормах (Л 1) приведены формулы для расчета перемещений, усилий и напряжений в элементах, выполненных в виде тонкостенных оболочек вращения постоянной толщины: цилиндрической короткой, полубесконечной и бесконечной оболочек; сферической без отверстия и с отверстием в вершине; полуэллиптической оболочки без отверстия. При этом рассмотрены осесимметричные нагрузки: внутреннее равномерное и гидростатическое давление, неравномерное вдоль меридиана и по толщине температурные нагрузки и краевые нагрузки.
В таблице 5 приведены расчетные формулы для самых распространенных случаев.
Эти формулы могут быть применены как к отдельным элементам, так и для сосудов (или других конструкций) составленных из разных элементов (цилиндрических, сферических, эллиптических и т.д.).
При действии на элемент нескольких видов усилий (внутреннее давление, температурное и краевые) перемещение элемента определяется путем сложения значений перемещений, вычисленных для каждой из действующих на элемент нагрузок. Например, для элемента 1 (рис.5.16) можно записать, что
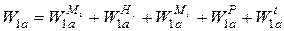
Система сил, действующих на элемент, может приводиться к одной силе и к одному моменту. Например, система сил 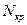 ,
, 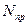 ,
, 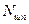 и
и 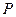 (рис.5.16) приведена к силе
(рис.5.16) приведена к силе 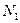 и моменту М.
и моменту М.
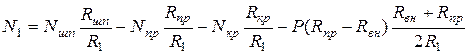
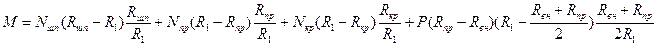
где 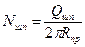 - продольная сила, приложенная к фланцу от шпилек, кг/мм;
- продольная сила, приложенная к фланцу от шпилек, кг/мм;
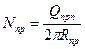 - сила, приложенная к фланцу от прокладки, кг/мм;
- сила, приложенная к фланцу от прокладки, кг/мм;
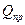 ,
, 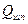 - усилия на шпильках и прокладке, кг.
- усилия на шпильках и прокладке, кг.
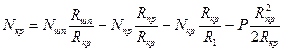 - сила, приложенная от крышки, кг/мм;
- сила, приложенная от крышки, кг/мм;
Н – перерезывающие усилия в стыке элементов, кг/мм.
Для рассматриваемого примера (рис.5.16) можно записать следующую систему уравнений совместимости деформаций:
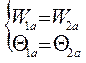
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 744; Нарушение авторских прав?; Мы поможем в написании вашей работы!