Методи математичного опису елементів і систем управління

Типи моделей.

Моделі можна розрізняти по ряду ознак: характеру модельованих об'єктів, сферам додатка, глибині моделювання, засобів моделювання. За останньою ознакою методи моделювання поділяються на дві групи: матеріальне (предметне) і ідеальне.

Матеріальне моделювання, що грунтується на матеріальній аналогії модельованого об'єкта й моделі, здійснюється за допомогою відтворення основних геометричних, фізичних, інших функціональних характеристик досліджуваного об'єкта. Окремим випадком матеріального моделювання є фізичне моделювання, стосовно якого, в свою чергу, приватним випадком є ​​аналогове моделювання. Воно засноване на аналогії явищ, що мають різну фізичну природу, але описуваних однаковими математичними співвідношеннями. Приклад аналогового моделювання - вивчення механічних коливань за допомогою електричної системи, описуваної тими ж диференціальними рівняннями. Так як експерименти з електричною системою звичайно простіше і дешевше, вона досліджується як аналог механічної системи.

Ідеальне моделювання відрізняється від матеріального принципово. Воно засноване на ідеальній, чи мислимій, аналогії. В економічних дослідженнях це основний вид моделювання. Ідеальне моделювання, у свою чергу, розбивається на два підкласи: знакове (формалізоване) і інтуїтивне.

Інтуїтивне моделювання зустрічається в тих областях науки, де пізнавальний процес знаходиться на початковій стадії або мають місце дуже складні системні взаємозв'язки. Такі дослідження називають уявними експериментами. В економіці до останнього часу в основному застосовувалося інтуїтивне моделювання; воно описує практичний досвід працівників.

При знаковому моделюванні моделями служать схеми, графіки, креслення, формули. Найважливішим видом знакового моделювання є математичне моделювання, здійснюване коштами логіко-математичних побудов.

Аналіз процесів, що відбуваються в системах, і ефективне вирішення завдань розрахунку, проектування і конструювання систем і пристроїв можливі лише із застосуванням мови і методів математики. Причому першим етапом при дослідженні або конструюванні системи є складання математичного опису (математичній моделі) її елементів і системи в цілому.

Складання математичного опису конструктивного елемента системи складається з наступних послідовних процедур:

• 
  прийняття вихідних припущень;
• 
  вибір вхідних і вихідних змінних;
• 
  вибір систем відліку для кожної змінної;
• 
  застосування фізичного, економічного чи іншого принципу, що відображає в математичній формі закономірності протікання процесу.

Найбільш поширеною, а також найбільш загальною і повною формою опису передавальних властивостей систем (автоматичних систем) та їх елементів є звичайні диференціальні рівняння. Для більшості реальних елементів вихідне рівняння, складене строго відповідно до законів фізики, виявляється нелінійним. Ця обставина сильно ускладнює всі наступні процедури аналізу. Тому завжди прагнуть перейти від важко розв'язні нелінійного рівняння до лінійного диференціального рівняння, зазвичай записуваного в символічній або операторній формі, виду

(A ₀ p ⁿ + a ₁ p ^n-1 +... + a _n) y (t) = (b ₀ p ^m + b ₁ p ^m-1 +... + b _m) x (t), (1.1)

де: x (t) і y (t) - відповідно вхідна і вихідна величини елемента або системи;

a _i, b _i - коефіцієнти рівняння;

p - оператор, скорочене умовне позначення операції диференціювання: d / dt = p.

Ще одним з поширених методів опису і аналізу автоматичних систем є операційний. В основі методу лежить перетворення Лапласа

X (p) = L [x (t)] = x (t) ^e-pt dt, (1.2)

яке встановлює відповідність між функціями дійсної змінної t і функціями комплексної змінної p.

Функціональні елементи, використовувані в системах управління, можуть мати саме різне конструктивне виконання і самі різні принципи дії. Однак спільність математичних виразів, що зв'язують вхідні і вихідні величини різних функціональних елементів, дозволяє виділити обмежене число так званих типових алгоритмічних ланок. Кожному такому ланці відповідає певне математичне співвідношення між вхідний і вихідний величинами. Якщо це співвідношення є елементарним (наприклад, диференціювання, множення на постійний коефіцієнт), то і ланка називається елементарним.

Алгоритмічні ланки, які описуються звичайними диференціальними рівняннями першого і другого порядку, отримали назву типових динамічних ланок. Найбільш часто зустрічаються ланки: безінерційною (пропорційне), інерційне першого порядку (аперіодичне), інерційне другого порядку (аперіодичне або коливальний), інтегруюче, дифференцирующее, изодромную (пропорційно-інтегруючий), форсує (пропорційно-дифференцирующее), інтегро-дифференцирующее (з переважанням інтегруючих або дифференцирующих властивостей), запізнюється.

Наведемо приклади реальних пристроїв, які відповідають визначенню типового динамічної ланки.

Типовий приклад безінерційного ланки, що є найпростішим серед усіх типових ланок, - редуктор. Його передавальні властивості описуються алгебраїчним рівнянням

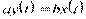(1.3)

або

, (1.4)

де k = b / a - Передавальний коефіцієнт редуктора, який залежить від співвідношення діаметрів або чисел зубів веденої і ведучої шестерень.

Реальними інтегруючими ланками є електричні виконавчі двигуни постійного і змінного струму. Диференціальне рівняння (в операторній формі) ідеального інтегруючого ланки виглядає наступним чином:

, (1.5)

де k - коефіцієнт пропорційності, що залежить від конструктивних параметрів пристрою.

Запізнілих ланка передає сигнал з входу на вихід без спотворення його форми. Однак всі миттєві значення вхідної величини вихідна величина приймає з деяким відставанням (запізненням). Здатністю затримувати сигнал у часі, не змінюючи його форми, володіють багато елементів промислових автоматичних систем. У першу очкредь до таких елементів відносяться транспортуючі пристрої - конвеєри ітрубопроводи.

Рівняння запізнілого ланки

, (1.6)

- час запізнювання.tде

В операційній формі передавальна функція запізнілих ланки виглядає наступним чином:

(1.7)

Якщо запізнюється ланка входить в контур системи управління, то характеристичне рівняння системи буде вже не простим алгебраїчним, а трансцендентним. Рішення і аналіз трансцендентних рівнянь пов'язані з великими труднощами. Тому часто в практичних розрахунках трансцендентну передатну функцію (1.7) розкладають в ряд Пада і, враховуючи тільки перші два члени ряду, наближено замінюють її дрібно-раціональної функцією:

(1.8)

Запізнілі ланки в більшості випадків погіршують стійкість систем і роблять їх важко керованими.

На закінчення необхідно відзначити, що методика аналізу, заснована на розчленовуванні системи на типові ланки, широко увійшла в практику інженерних розрахунків, виконуваних у процесі конструювання, і в даний час є домінуючою.

Дата добавления: 2013-12-13