Влияние сил инерции на движение вблизи поверхности Земли

ЛЕКЦИЯ 19 - 2011

Влияние силы инерции Кориолиса на свободное падение тел вблизи поверхности Земли. Пусть тело свободно падает в гравитационном поле Земли. Его ускорение относительно Земли, обусловленное всеми силами, равно

величина - угловая скорость суточного вращения Земли. Последнее слагаемое в правой части уравнения учитывает влияние силы Кориолиса. Поскольку эта сила перпендикулярна скорости тела, она не совершает работы, не может изменить величину скорости (и кинетической энергии), а способна только искривить траекторию движения. Покажем, что при падении тел без начальной скорости кориолисова сила проявляется в отклонении свободно падающих тел к востоку и к экватору от направления отвеса (определяемого вектором).

При расчетах, будем предполагать величину ускорения свободного падения постоянной (не зависящей от положения тела). Это предположение оправдано достаточно малым изменением расстояния тела до земли в процессе движения и, следовательно, достаточно малым временем полета (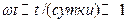). В этих условиях влияние силы Кориолиса достаточно слабое, и его можно учесть посредством метода последовательных приближений.

В выражении для ускорения член мал по сравнению с. Поэтому его можно рассматривать как малую поправку и в нулевом приближении отбросить:

Используя это приближение, можно учесть в первом приближении влияние силы Кориолиса

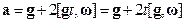
Интегрируя это уравнение при нулевой начальной скорости, получаем в этом же приближении

С помощью этого выражения снова уточняем влияние кориолисовой силы на ускорение (второе приближение теории возмущений)

Интегрируя это уравнение, получаем уточненное выражение для скорости во втором приближении теории возмущений

и т.д. Прервем процесс последовательных приближений на этом этапе, ограничившись полученным нами вторым приближением по учету кориолисовой силы. Интегрируя выражения для скорости, найдем перемещение тела из начальной точки

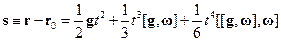
Чтобы проанализировать полученный результат введем декартову систему с полюсом в начальной точке падения тела. Ось ОХ направим по параллели на восток, ось ОY – по меридиану к экватору, ось OZ направим по направлению отвеса вниз, т.е. вдоль вектора . Разложим стоящие в формулах векторные произведения на эти координатные оси.

Проекции вектора перемещения на те же оси

где – угол географической широты рассматриваемого места. Влияние силы Кориолиса на координатную составляющую по направлению отвеса (ось Z) дает только маленькую поправку к нулевому приближению. Ее можно отбросить и найти время падения из нулевого приближения

где h – высота падения.

Однако влияние кориолисовой силы на направления, перпендикулярные отвесному, отбросить нельзя, т.к. в нулевом приближении эти проекции равны нулю. Таким образом, вращение земли сказывается в появлении двух новых эффектов: в отклонении свободно падающих тел к востоку и к экватору от направления отвеса (вдоль осей OX и OY). Величина восточного отклонения

Здесь – период суточного вращения Земли. Отклонение мало, поскольку в него входит малый множитель . Так, при =100 м =4,5c на широте 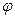≈60^о получаем 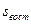=1,2 см. При падении с высоты h=500м получилось бы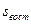=13,8 см. Несмотря на малость эффекта его с уверенностью удалось наблюдать в глубоких шахтах уже в середине XIX века.

Экваториальное отклонение связано с восточным соотношением

т.е. оно на порядок величины меньше восточного и невозможно наблюдению.

Маятник Фуко.

Более наглядным проявлением силы Кориолиса является поворот плоскости (малых) колебаний тяжелого тела, подвешенного на длинной нити – маятника Фуко. В инерциальной системе такой маятник, двигаясь под действием силы тяжести и силы натяжения нити, совершает колебания в одной плоскости. Однако в земной системе отсчета плоскость качаний маятника медленно поворачивается вокруг вертикали рассматриваемого места, причем, в том же направлении, в каком совершают суточное вращение Солнце и звезды на небесной сфере. Это является еще одним доказательством неинерциальности земной системы отсчета.

Допустим, что опыт с маятником Фуко поводится на полюсе Земли (), где направление отвеса совпадает с осью земного вращения. В любой инерциальной системе отсчета, содержащей ось вращения Земли, маятник колеблется в одной плоскости. Но Земля вращается вокруг этой плоскости с угловой скоростью . Следовательно, относительно Земли плоскость качаний маятника вращается в противоположную сторону с такой же по величине скоростью ω.

Пусть теперь опыт проводится в точке земной поверхности с географической широтой 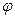. В этой точке направление отвеса (местной вертикали) составляет с осью вращения Земли угол 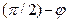. Разложим вектор угловой скорости вращения Земли на две составляющие: вертикальную(по направлению отвеса) и горизонтальную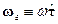 (в плоскости, ортогональной отвесу):

Покажем, что вращение плоскости качаний определяется только составляющей угловой скорости в направлении местной вертикали, в то время как горизонтальная составляющая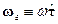не оказывает на этот эффект никакого влияния.

Динамическое уравнение движения маятника в геоцентрической системе отсчета:

Два средних члена обусловлены влиянием силы Кориолиса. Рассмотрим влияние составляющей этой силы . Разложим горизонтальную составляющую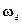на две составляющие, из которых одна лежит в плоскости качаний, а вторая– ортогональна этой плоскости: 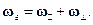Рассматриваемая составляющая силы Кориолиса разбивается при этом на две силы: Вращающий плоскость качаний эффект может создавать только та из них, которая перпендикулярна этой плоскости. Таковой является сила . Вторая составляющая силылежит в плоскости качаний и направлена вдоль линии маятника. Поэтому данная сила всего лишь слегка меняет натяжение нити, а с ней и период колебаний. Составляющая кориолисовой силыхотя и ортогональна плоскости качаний, но оказывает на нее слабое влияние. Во-первых, вектор составляет малый угол с вектором скорости. Во-вторых, при колебаниях маятника вектор периодически меняет свое направление: при движении маятника вправо или влево от положения равновесия он направлен в одну сторону, а при движении из крайних положений к центру – в противоположную. Поэтому сила не приводит к систематическому вращению плоскости колебаний, а вызывает лишь малые колебания ее относительно среднего положения. Следовательно, эту силу также можно не учитывать.

Таким образом, при исследовании эффекта вращения плоскости качаний маятника составляющую силы Кориолиса можно отбросить. Под действием оставшихся сил уравнение относительного движения принимает вид

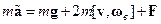
Это уравнение имеет такой же вид, что и на полюсе. Разница только в том, что вместо полной угловой скоростив нем фигурирует ее составляющая на положение отвеса. Следовательно, поведение плоскости качаний маятника будет таким же, как на полюсе, однако скорость вращения плоскости будет происходить с меньшей угловой скоростью

Полный оборот плоскость качаний совершает за время

где – период вращения земли в инерциальной системе отсчета. На полюсах период обращения плоскости качаний равен периоду обращения Земли вокруг своей оси, т.е. одним суткам. Качание маятника в экваториальной плоскостине сопровождается поворотом плоскости качаний, поскольку в этом случае направление отвеса ортогонально вектору угловой скорости вращения Земли:

Реальный опыт был произведен Фуко в Парижской обсерватории в 1850 году и повторен в 1851 году в Пантеоне. Маятник имел длину 67 м и состоял из металлического шара массой m=28 кг.

Рассмотрим более детально искривление траектории движения маятника под действием силы Кориолиса. Поскольку ось вращения Земли ориентирована с Юга на Север, действующая на Земле сила Кориолиса 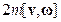является «правшой»: она отклоняет движущиеся относительно Земли тела вправо по ходу их движения. (Например, тело, движущееся по меридиану с Юга на Север, кориолисова сила отклоняет на Восток, а тело, движущееся в обратном направлении – на Запад). Повернем ось вращения Земли так, чтобы плоскость рисунка демонстрировала проекцию на землю траектории движения маятника, причем так, как она видна наблюдателю, стоящему на земле, т.е. наблюдающему эту проекцию «сверху вниз». Эта ситуация соответствует повороту полярной оси «на нас», т.е. вращению Земли на рисунке против часовой стрелки. При этом на рисунке будет отображаться линия, которую вычерчивал бы на земле заостренный выступ шарообразного маятника.

Пусть в начальном состоянии маятник был максимально отклонен от положения равновесия. Тогда при каждом периоде колебаний сила Кориолиса 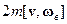загибает его траекторию вправо по ходу движения маятника. После каждого периода качаний маятник не возвращается в исходное состояние, а сдвигается по ходу часовой стрелки. В результате, отрезок, соединяющий амплитудные положения маятника, все время поворачивается по ходу часовой стрелки, т.е. в направлении, противоположном вращению земли (см. рисунк). Поворот рассматриваемого отрезка отражает поворот плоскости качаний маятника под действием силы Кориолиса.

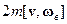Несколько иной характер траектории получается, когда маятнику сообщен толчок из положения равновесия. Траектория по-прежнему изгибается вправо по ходу маятника. Но в крайних точках (местах поворота маятника) возникают не точки заострения, а плавные закругления. Они возникают за счет того, что в точках поворота скорость маятника теперь не обращается в нуль (как это имело место в предыдущем случае), а имеет азимутальную составляющую, приобретенную под действием кориолисовой силы при движении от центра. Однако, вследствие медленности вращения Земли, наблюдатель не замечает этих нюансов в поведении маятника. В обоих случаях ему кажется, что плоскость качаний маятника вращается вокруг вертикали с угловой скоростью .

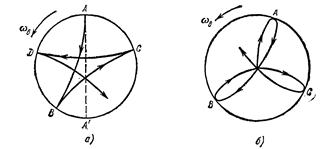
а) траектория маятника при запуске без толчка из максимально удаленного положения; б) траектория маятника при запуске толчком из положения равновесия

Дата добавления: 2013-12-13