
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства логических операций
Логические операции над высказываниями.
Логической операцией над высказываниями называется построение нового высказывания из исходных высказываний.
Основой цифровой техники служат три логические операции, лежащие в основе всех выводов компьютера: логическое отрицание НЕ, логическое умножение И, логическое сложение ИЛИ. Иногда эти операции называют "тремя китами машинной логики". С помощью этих операций можно описать все остальные. Такие операции называются функционально полным набором.
Познакомимся с ними подробнее.
1. Логически отрицанием или инверсией (NOT Х, не  ) высказывания Х называется новое высказывание
) высказывания Х называется новое высказывание  , которое является истинным, если Х ложно и ложью, если Х – истинно. Другое обозначение: ⌐Х.
, которое является истинным, если Х ложно и ложью, если Х – истинно. Другое обозначение: ⌐Х.
На структурных схемах данную логическую функцию обозначают с помощью следующего символа:
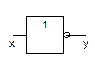
2. Логическим умножением или конъюнкцией (Х AND У, ХУ, Х&У, Х  У) двух высказываний Х и У называется новое высказывание, которое является истинной только при истинности обоих высказываний Х и У и ложью, если хотя бы одно из высказываний Х или У ложно.
У) двух высказываний Х и У называется новое высказывание, которое является истинной только при истинности обоих высказываний Х и У и ложью, если хотя бы одно из высказываний Х или У ложно.
На схемах эта функция обозначается с помощью символов: или
или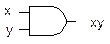
3. Логическим сложением или дизъюнкцией (Х OR У, Х+У, Х 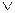 У) двух высказываний Х и У называется новое высказывание, которое является истинной если хотя бы одно из высказываний Х или У истинно, и ложью только в случае ложности как Х так и У.
У) двух высказываний Х и У называется новое высказывание, которое является истинной если хотя бы одно из высказываний Х или У истинно, и ложью только в случае ложности как Х так и У.
На схемах эта функция обозначается с помощью символов: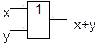 или
или
4. Импликацией (Х → У) двух высказываний Х и У называется новое высказывание, которое будет ложным только в случае, когда Х - истинно, а У - ложно, и истинным во всех остальных случаях.
В высказывании Х → У Х часто называют посылкой, а У – заключением.
5. Эквиваленицией (Х ↔ У, Х ~ У) двух высказываний Х и У называется новое высказывание, которое будет истинным только в случае, когда оба высказывания Х и У одновременно истинны или одновременно ложны, и ложным во всех остальных случаях.
6. Исключающее ИЛИ (Х ХOR У, 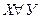 ) двух высказываний Х и У называется новое высказывание, которое будет истинным только в случае, когда высказывания Х и У имеют разное значение, и ложным во всех остальных случаях.
) двух высказываний Х и У называется новое высказывание, которое будет истинным только в случае, когда высказывания Х и У имеют разное значение, и ложным во всех остальных случаях.

 Кроме перечисленных основных логических операций имеются более редко используемые: штрих Шеффера Х|У, стрелка Пирса Х↓У и другие.
Кроме перечисленных основных логических операций имеются более редко используемые: штрих Шеффера Х|У, стрелка Пирса Х↓У и другие.
На схемах стрелка Пирса обозначается с символом:, а штрих Шеффера
Действие логических операций иллюстрируется таблицей истинности (Х, У - операнды логического типа):
| Х | У | 
| Х  У У
| Х 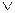 У У
| ХХOR У | Х → У | Х ↔ У | Х|У | Х↓У |
Используя основные логические операции можно построить более сложные высказывания, например: 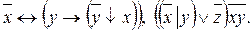
Указанные высказывания называются формулами алгебры высказываний. Эти формулы состоят из простых высказываний, знаков логических операций, а также скобок. Скобки указывают последовательность выполнения операций. Приоритет операций: первыми выполняются операции в скобках, затем отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Две формулы алгебры высказываний A и B называются равносильными, если они принимают одинаковые логические значения на любом наборе значений элементарных высказываний, входящих в формулы. Обозначение: А≡В.
Формула А называется тождественно-истинной или тавтологией, если она принимает значение «истинно» при всех значениях переменных, входящих в нее.
Формула В называется тождественно-ложной или противоречием, если она принимает значение «ложь» при всех значениях переменных, входящих в нее.
Упражнение: доказать, что
1) x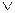 (x→(y→x)) – тавтология
(x→(y→x)) – тавтология
2) (x↔ )
)  (x
(x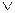 y→x) - противоречие
y→x) - противоречие
Логические операции обладают следующими свойствами:
1. Снятие двойного отрицания (отрицание противоречия): 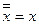 2. Коммутативность:
ху=ух
х+у=у+х
3. Ассоциативность:
(ху)z=x(yz)
(x+y)+z=x+(y+z)
4. Дистрибутивность:
x(y+z)=xy+xz
x+yz=(x+y)(x+z)
5. Идемпотентность:
x+x=x
xx=x
6. Законы де Моргана:
2. Коммутативность:
ху=ух
х+у=у+х
3. Ассоциативность:
(ху)z=x(yz)
(x+y)+z=x+(y+z)
4. Дистрибутивность:
x(y+z)=xy+xz
x+yz=(x+y)(x+z)
5. Идемпотентность:
x+x=x
xx=x
6. Законы де Моргана:

 7. Закон противоречия:
7. Закон противоречия:  8. Закон исключения третьего:
8. Закон исключения третьего: 
| 9. Законы поглощения:

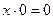

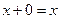
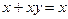
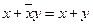

 10. Преобразование стрелки Пирса:
10. Преобразование стрелки Пирса:  11. Преобразование штриха Шеффера:
11. Преобразование штриха Шеффера: 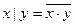 12.
12.  13. Закон контрапозиции:
13. Закон контрапозиции:


|
С помощью приведенных здесь формул можно упрощать логические выражения, т.е. уменьшать количество формул и операций в них. При этом следует стремиться к тому, чтобы результат содержал только операции отрицания, логического умножения и логического сложения. На самом деле эффективное использование указанных формул требует навыков и искусства в манипулировании ими, которые приходят только после определенного опыта подобных преобразований. В то же время существует несколько стандартных приемов, которые в большинстве случаев позволяют упростить достаточно сложные логические формулы.
Упрощение логического выражения начинают обычно с поиска следующих форм:  ,
,  ,
, 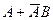 , где
, где 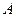 и
и 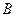 обозначают либо сами логические переменные, либо логические произведения множества переменных. Каждое из полученных выражений может быть записано в более простой форме следующим образом:
обозначают либо сами логические переменные, либо логические произведения множества переменных. Каждое из полученных выражений может быть записано в более простой форме следующим образом:
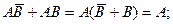
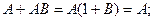

Пример 1. Возьмем, например, формулу:

и попытаемся ее упростить, используя изученные тождества. Группируя первый и четвертый термы, затем третий и пятый, получим:

Далее выражение упрощается без особой сложности:

Пример 2. Упростить логическую функцию  . Упрощенный вид должен содержать не более трех логических операций.
. Упрощенный вид должен содержать не более трех логических операций.



Имеются также и другие методы упрощения логических функций, одним из которых является метод, использующий специальные таблицы, называемые карты Карно.
|
|
Дата добавления: 2013-12-13; Просмотров: 3822; Нарушение авторских прав?; Мы поможем в написании вашей работы!