Преобразование Лапласа

Преобразованием Лапласа называют соотношение:

,

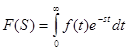ставящее функции f (t) вещественного переменного в соответствие функцию F(S) комплексного переменного S.

. При этом f (t) – оригинал, F(S) – изображение по Лапласу.

Иногда пользуются символической записью F(S)=L[ f ],

где L[ f ] – оператор Лапласа.

Предполагается, что функция f (t), которая подвергается преобразованию Лапласа, обладает следующими свойствами:

1) f (t) определена и кусочно-дифференцируема на всей положительной числовой полуоси [0, ∞];

2) f (t)=0 при t<0;

3) f (t) должна быть ограничена.

Соотношение:

называют обратным преобразованием Лапласа. Символически обратное преобразование Лапласа можно записать так:

где L^-1 - обратный оператор Лапласа.

Отметим основные свойства преобразования Лапласа:

1. Свойство линейности.

для любых и постоянных a₁ и a₂

2. Дифференцирование оригинала.

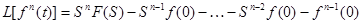
При нулевых начальных условиях, т.е.

то формула принимает вид:

3. Смещение изображения.

4. Свойство изменения масштаба (свойство подобия).

Принцип однородности, который лег в основу свойства линейности:

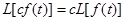
Приведем таблицу наиболее часто встречающихся функций с уже выведенными изображениями:

Таблица 1

Оригинал f (t)		sinat	cosat	e^±αt	t^n
Изображение F(S)

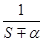
Пример. Пусть дано изображение:

Найти оригинал.

Преобразуем выражение:

Применяя свойства, описанные выше, и таблицу 1 получим оригинал:

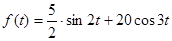
Дата добавления: 2013-12-13