Химический потенциал и давление пара у искривленных поверхностей

Рассмотрим малую сферическую каплю жидкой фазы α в фазе пара β. Используя уравнение для потенциала Гиббса для объемной фазы α при постоянных p и T, запишем:

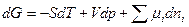. 4.4.1

, ;

, .

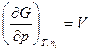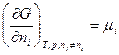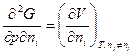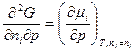Отсюда находим интересующую нас производную

, 4.4.2

где – парциальный мольный объем i -го компонента.

В процессе образования кривизны в однокомпонентной (i =1) двухфазной (α, β) системе при T, s и n_i = const получим:

4.4.3

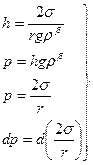4.4.4 (см.§3)

Подставляя 4.4.4 в 4.4.3, получим:

, 4.4.5

в первом приближении можно считать постоянной.

Так как для воды при r = 10^–7 м и σ = 73∙10^–3 Н/м можно найти p = 1,5 МПа (15 атм). Эта величина мала по сравнению с внутренним давлением воды (≈10³ МПа), и поэтому справедливо допущение, что в процессе искривления поверхности дополнительного сжатия жидкости не происходит.

Проинтегрируем выражение 4.4.5 в пределах от плоской поверхности (радиус r=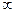) до искривленной поверхности (радиус r). вынесем за знак интегрирования, т.к. считаем ее постоянной.

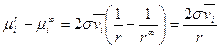, 4.4.6

где 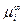– значение вещества у плоской поверхности.

Из уравнения 4.4.6 следует, чтов капле выше, чем у плоской поверхности. Но в состоянии равновесия , тогда, относя в уравнении 4.4.6 левую часть к пару, а правую – к жидкости, можно записать для идеальной системы

. 4.4.7

Над плоской поверхностью

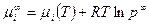. 4.4.8

Подставим 4.4.7 и 4.4.8 в выражение 4.4.6:

, 4.4.9

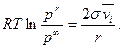4.4.10

Уравнение 4.4.10 называется уравнением Томсона (лорда Кельвина). Оно показывает, что давление насыщенного пара над каплей будет тем больше, чем больше σ и меньше радиус капли r.

Например, для воды при изменении радиуса от 10^–5 см до 10^–6 см давление увеличивается на 1 %. Это следствие уравнения Томсона (Кельвина) позволяет предсказать наблюдаемое явление изотермической перегонки, заключающееся в испарении малых капель и конденсации пара на более крупных каплях, а также на плоской поверхности.

Над вогнутым мениском жидкости В этом случае радиус кривизны меняет знак, и для сферического мениска получается аналогичное уравнение

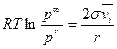. 4.4.11

Дата добавления: 2013-12-13