ЛЕКЦИЯ № 6

ЭМВ В Различных средах

Учебные вопросы:

1. Электродинамические потенциалы.

2. Распространение ЭМВ в неограниченных изотропных средах.

3. эмв в идеальном диэлектрике.

ВВЕДЕНИЕ

На основе материала предыдущей лекции рассмотрим отличия в распространении плоской ЭМВ в среде, обладающей некоторой проводимостью, а следовательно, и потерями. При этом рассмотрим изменение скорости переноса энергии волны в зависимости от частоты и явление экранирования.

1 Электродинамические потенциалы

Напомним, что в теории статических полей вводятся вспомогательные функции: скалярный потенциал электрического поля 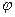и векторный потенциал магнитного поля 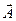таким образом, что:

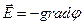, (1)

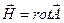, (2)

В электродинамике для описания электромагнитных полей тоже вводятся скалярный 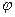и векторный 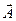электродинамические потенциалы. Введение потенциалов электромагнитного поля позволяет значительно облегчить решение ряда задач электродинамики. В начале этой главы мы уже говорили о том, что потенциалы определяют энергию заряженной частицы в электромагнитном поле, напряженность поля определяет силу, с которой поле действует на частицу. Сила, которая действует на частицу, движущуюся в электрическом и магнитном полях, определяется формулой:

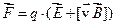(3)

где q – заряд частицы, v – её скорость.

Формула (3.3.3) носит название формулы Лоренца. Она широко используется при динамическом расчете движения заряженных частиц (электронов или ионов) в электрическом и магнитном полях. При решении задач квантовой механики силы, действующие на частицы, как правило, в расчет не принимаются. Для расчета квантовых состояний частиц в электрическом и магнитном полях в соответствующие уравнения вводятся скалярный 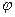и векторный 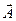электродинамические потенциалы.

Роль, которую играют потенциалы 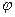и 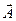в электродинамике и квантовой механике, хорошо описана в уже упомянутых Фейнмановских лекциях по физике (том 6 «Электродинамика» и том 9 «Квантовая механика» изд. «Мир», Москва 1966 и 1967 гг.).

Рассмотрим, как потенциалы 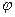и 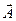связаны с векторами напряженности электрического и магнитного полей, и найдем уравнения, которым удовлетворяют эти потенциалы. Для этого будем использовать уравнения Максвелла.

Зададим векторный потенциал 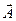так, как это делается для статических полей (2). Подстановка (2) в уравнение Максвелла:

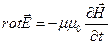
приводит к следующему равенству:

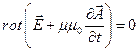. (4)

Используя тождество векторной алгебры 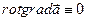, функцию, стоящую в (4) в скобках, можно приравнять градиенту некоторого скаляра.

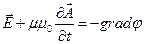. (5)

Разумно положить, что этот скаляр есть скалярный потенциал электрического поля. Тогда в статическом случае, когда производная по времени рана нулю, соотношение (5) превращается в уже принятое соотношение (1).

Таким образом, мы поучили выражение для напряженности электрического поля, изменяющегося во времени:

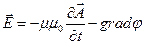(6)

Согласно выражению (3.3.6), напряженность электрического поля может быть разделена на вихревую и потенциальную части, причем вихревая часть имеет место только в случае изменяющихся во времени полей.

Таким образом, напряженности поля 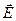и 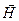выражаются через электродинамические потенциалы 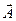и 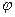с помощью соотношений (2) и (6), и для описания электромагнитных полей достаточно знать 4 потенциальные функции: три проекци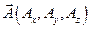и и .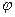

Получим дифференциальные уравнения для электродинамических потенциалов 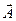и 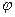. Для этого в уравнения Максвелла

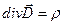
подставим выражения (2) и (6)

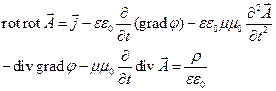(7)

Воспользуемся известным соотношением векторной алгебры: 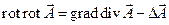. Тогда (7) можно переписать так:

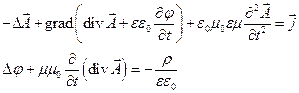(8)

Дифференциальные уравнения (8) связывают электродинамические потенциалы (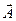и 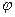) с источниками: зарядами и токам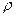и (и ).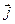

Наложим дополнительное условие, позволяющее разделить уравнения для потенциалов:

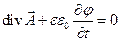(9)

Это условие (9) называется условием калибровки Лоренца. Используя калибровку Лоренца, можем систему уравнений (8) переписать в более простом виде:

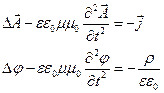(10)

Эти уравнения описывают те же физические процессы, которые описывают уравнения Максвелла. Система уравнений (10) образована двумя уравнениями. Такое разделение уравнений оправдано физически: в уравнение для 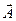входит плотность тока, (токи являются источниками магнитных полей), а в уравнение для 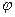входит плотность зарядов, (заряды являются источниками и стоками электрического поля). Уравнения (10) могут быть записаны как 4 скалярных дифференциальных уравнения для потенциалов с одинаковой формой для всех четырех функций 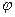,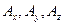. 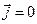При и 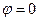уравнения (10) переходят в волновые уравнения, которые для гармонических колебаний примут вид:

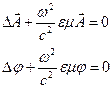(11)

В отсутствии временной зависимости 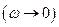уравнения (11) переходят в уравнения магнитостатики и уравнения Пуассона

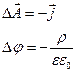(12)

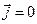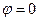При отсутствии источников (и ) уравнения Пуассона превращаются в уравнения Лапласса

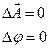(3)

В отсутствии временной зависимости 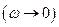калибровка Лоренца (9) принимает следующий вид:

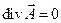(14)

и носит название «калибровка Кулона».

При решении задач техники СВЧ, как правили, бывает достаточно решить задачу относительно одной из четырех функций координат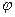,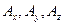. Выбранная функция является скаляром, что сильно упрощает решение используемых дифференциальных уравнений. Подчеркнём здесь, что решение дифференциальных уравнений требует формулировки граничных условий. В следующих главах нашего курса мы будем рассматривать различные волноведущие структуры и находить их свойства путем решения дифференциальных уравнений относительно одной из названных выше четырех функций координат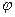,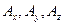. При решении этих задач мы будем формулировать необходимые граничные условия. Получив решение относительно избранного электродинамического потенциала, компоненты векторов электрического и магнитного полей можно найти с помощью приведенных выше соотношений (2) и (6).

Еще один векторный потенциал

При решении некоторых задач техники СВЧ заранее известно, что электрическое поле носит вихревой характер, то есть скалярный потенциал

j = 0. При этом из (6) и (9) получаем:

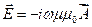(15)

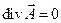(16)

Вспоминая, что div(rot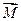) = 0, где 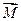произвольная векторная функция, можем заключить, что из (16) и (15) следует, что

. (17)

Здесь вектор 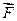представляет собой «электрический» векторный потенциал в отличие от традиционного «магнитного» векторного потенциала 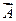. Подставляя (17) в уравнения Максвелла, найдем, что вектор 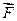, как и вектор 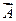, удовлетворяет волновому уравнению. Найдя решение волнового уравнения для одной из компонент F_x, F_y, F_z, находим компоненты вектора напряженности электрического поля с помощью соотношения (17) и далее компоненты вектора напряженности магнитного поля с помощью соответствующего уравнения Максвелла. В определенных случаях использование «электрического» векторного потенциала 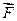облегчает решение соответствующих электродинамических задач.

2. Распространение ЭМВ в неограниченных изотропных средах

ИЗОТРОПНАЯ СРЕДА, среда, обнаруживающая во всех направлениях одинаковые физические свойства, например теплопроводность, упругость, электропроводность и др. К изотропным средам относятся аморфные тела: воздух, вода, непрессованное стекло, сплавы и др. Свойства же кристаллических тел различны в различных направлениях (см. Анизотропия). Однако кристаллы правильной системы в отношении некоторых свойств (скорости распространения света, электропроводности, теплопроводности и др.) оказываются изотропными.

Решение задачи о распределении электрического поля в однородной изотропной и безграничной среде (cм. рис.) может быть получено путем интегрирования дифференциального уравнения Лапласа

div σ (grad φ) = Δ φ = 0.

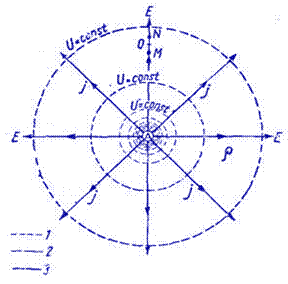
Рис. 1

В однородной среде, вследствие сферической симметрии, потенциал φ любой точки М, удаленной на расстоянии R oт начала координат, не зависит от полярного угла θ и азимутального угла φ^/. Уравнение Лапласа примет более простой следующий вид

3. эмв в идеальном диэлектрике

Найдем решение уравнений Масквелла для простейшего случая распространения электромагнитной волны в идеальном диэлектрике.

В вакууме 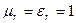, 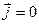. Поэтому для идеального диэлектрика уравнения Максвелла принимают вид:

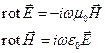(1.3.5)

Исключим 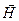из (1.3.5). Для этого применим операцию rot к обеим частям первого уравнения: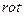 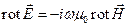. Теперь подставим значение 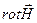из второго уравнения. В результате получим:

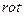
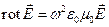(1.3.6)

Используем известное соотношение векторной алгебры

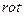
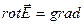
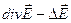(1.3.7)

Вспомним, что в соответствии с теоремой Гаусса-Остроградского

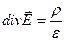(1.3.8)

и учтем, что в вакууме свободных зарядов нет (т.е. 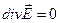). Подставим (1.3.8) и (1.3.7) в (1.3.6). В результате получаем:

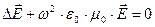(1.3.9)

Полученное уравнение носит название волновое уравнение. Аналогичным образом можно получить волновое уравнение относительно вектора магнитного поля .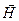

Наиболее наглядным решением волнового уравнения является сферическая волна, распространяющаяся вокруг точечного излучателя. Чтобы получить решение для сферической волны, нужно представить оператор Лапласа в уравнении (1.3.9) в сферической системе координат, что приведет к достаточно громоздким математическим выражениям. С целью упрощения математических процедур мы рассмотрим решение волнового уравнения для плоской волны, являющейся функцией одной координаты.

Рис.1.3.1. показана схема расположения силовых линий сферической электромагнитной волны. Рисунок иллюстрирует тот факт, что на больших расстояниях от излучателя электромагнитное поле можно рассматривать как плоскую волну, распространяющуюся вдоль направления, перпендикулярного плоскости постоянной фазы, причем характеристики волны зависят только от одной координаты вдоль направления распространения. Несмотря на то, что в общем случае волна имеет сферическую симметрию, в ограниченной области, обозначенной квадратом, можно говорить о плоской волне, характеристики которой зависят только от одной координаты.

Примем во внимание, что одномерный оператор Лапласа имеет следующий вид:

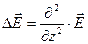(1.3.10)

и получим одномерное волновое уравнение для плоской волны:

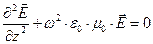(1.3.11)

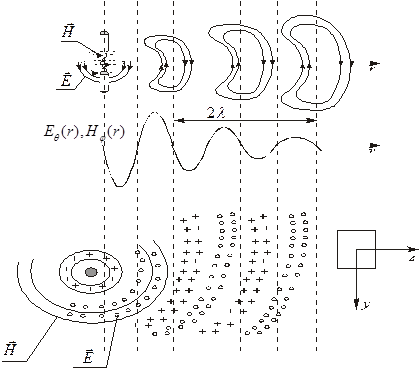
Рис.1.3.1. Схема силовых линий напряженности электрического и магнитного полей сферической электромагнитной волны.

Любое дифференциальное уравнение приобретает физический смысл, если заданы граничные условия для его решения. Решение уравнения (1.3.11) получается в виде двух волн, распространяющихся вдоль положительного и отрицательного направлений оси z. Примем в качестве граничных условий утверждение, что в рассматриваемой среде плоская волна может распространяться только в одном направлении. Итак, мы имеем решение уравнения (1.3.11) для плоской волны, распространяющейся вдоль положительного направления оси z:

(1.3.12)

Фаза волны:

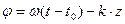, (1.3.13)

где k - волновое число (в общем случае волновой вектор).

Фиксированная ориентация вектора напряженности поля вдоль заданной координатной оси носит название поляризации волны. Соотношение (1.3.12) задает поляризацию напряженности электрического поля вдоль оси х.

На рис.1.3.2. показано положение плоскости постоянной фазы для двух моментов времени.

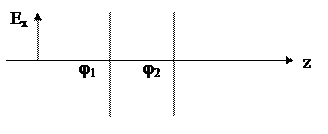
Рис.1.3.2. Движение плоскости постоянной фазы.

Для плоскости постоянной фазы(φ = const), которая движется вдоль оси z, ее производная по времени равна нулю:

;

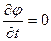в соответствии с (1.3.13) получаем: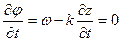

так что

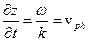, (1.3.14)

где 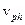— скорость движения поверхности неизменной фазы или фазовая скорость.

Подставив (1.3.12) в (1.3.11) получим

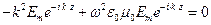, (1.3.15)

и, сократив 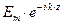, получим дисперсионное уравнение для плоской волны в свободном пространстве:

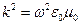, или 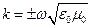(1.3.16)

Разные знаки в выражении для k соответствуют волнам, распространяющимся вдоль оси z в разных направлениях. В соответствии с (1.3.14):

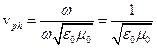(1.3.17)

В свободном пространстве 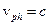, где c - скорость света.

Таким образом, из уравнений Максвелла следует, что скорость света в свободном пространстве определяется диэлектрической и магнитной проницаемостями вакуума:

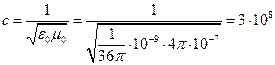м/с (1.3.18)

Диэлектрическая и магнитная проницаемость вакуума – это характеристики пространства, связанные со статическими полями. Первая из них характеризует только диэлектрические свойства среды. А вторая – только магнитные свойства. Результат решения уравнений Масквелла, представленный формулой (1.3.18), связывает воедино электростатику, магнитостатику и динамический процесс распространения света.

Действительно, диэлектрическую проницаемость можно получить экспериментально путем измерения силы взаимодействия двух известных зарядов q₁ и q₂ расположенных на расстоянии r друг от друга:

(закон Кулона).

Таким образом, из статического эксперимента можно получить численное значение .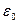

Магнитную проницаемость можно получить, измерив силу взаимодействия двух проводников длино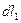й и 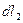с током 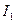и 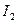соответственно, расположенных на расстоянии r друг от друга:

(закон Био-Савара-Лапласа)

Таким образом, из статического эксперимента можно получить численное значение .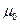

Следовательно, уравнения Максвелла позволяют выразить скорость света через характеристики, полученные с помощью статических измерений.

Уравнения Максвелла связывают воедино электрическое поле, магнитное поле и электромагнитные волны (свет). Создание концепции электромагнитного поля и формулировка уравнений, его описывающих, послужили одной из важнейших отправных точек физики XX века.

Дата добавления: 2013-12-13