
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦИЯ № 7
|
|
|
|
ЭМВ В СРЕДАХ С ПОТЕРЯМИ
Учебные вопросы:
1. Распространение плоских ЭМВ в среде с потерями.
2. Скорость распространения ЭМВ в различных средах. Дисперсия.
3. Поверхностный эффект.
ВВЕДЕНИЕ
На основе материала предыдущей лекции рассмотрим отличия в распространении плоской ЭМВ в среде, обладающей некоторой проводимостью, а следовательно, и потерями. При этом рассмотрим изменение скорости переноса энергии волны в зависимости от частоты и явление экранирования. Материал лекции имеет практическое значение и служит теоретической основой расчета потерь энергии сигнала при его распространении и построения экранов. Обратим внимание на вредное воздействие ЭМП на организм человека и способы защиты.
1. РАСПРОСТРАНЕНИЕ ПЛОСКИХ ЭМВ В СРЕДЕ С ПОТЕРЯМИ
Как ранее было отмечено, коэффициент распространения в средах с проводимостью становится комплексной величиной и может быть представлен в алгебраической 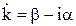
и показательной
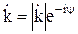 (1)
(1)
формах, причем
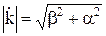 , (2)
, (2)
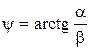 , (3)
, (3)
Среды с потерями (g¹0), в свою очередь, распределяются на диэлектрические, проводящие и среды, занимающие промежуточное положение. В диэлектрических средах 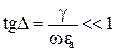 и тем более
и тем более 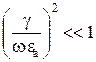 ,
,
поэтому можно пренебречь величиной 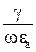 . В этом случае коэффициент фазы будет определяться выражением
. В этом случае коэффициент фазы будет определяться выражением
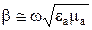 . (4)
. (4)
Однако такое же упрощение для a неприемлемо, так как обращает его в нуль, т.е. исключается возможность учета потерь на протяженных линиях радиосвязи. Из материала прошлой лекции:
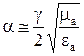 . (5)
. (5)
Величина фазового сдвига соответственно будет определяться выражением
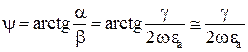 . (6)
. (6)
В проводящих средах:
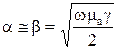 , (7)
, (7)
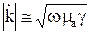 , (8)
, (8)
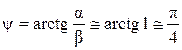 . (9)
. (9)
В средах, занимающих промежуточное положение между проводниками и диэлектриками, коэффициенты фазы и затухания определяются по полным формулам.
В средах с потерями волновое сопротивление становится комплексной величиной
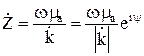 . (10)
. (10)
и для диэлектрических сред: 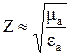 ; для проводящих сред:
; для проводящих сред: 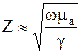 ,
,
и, соответственно, формулы поля плоской электромагнитной волны учетом выражения для волнового сопротивления могут быть представлены в виде:
в показательной форме комплексного изображения
 , (11а)
, (11а)
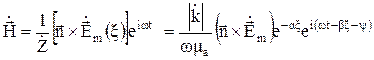 , (11б)
, (11б)
в тригонометрической форме
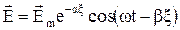 , (12а)
, (12а)
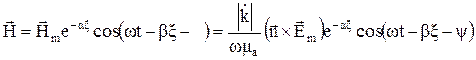 , (12б).
, (12б).
Из (11) и (12) следует, что поле плоской волны в среде с потерями обладает следующими свойствами:
1. Векторы Е и Н перпендикулярны друг другу и направлению распространения П волны, т.е. волна является поперечной, но между Е и Н появляется фазовый сдвиг 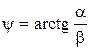 , который тем меньше, чем меньше коэффициент затухания a;
, который тем меньше, чем меньше коэффициент затухания a;
2. Амплитуды векторов Е и Н убывают по экспоненциальному закону с увеличением расстояния x;
3. Поверхности равных амплитуд совпадают с поверхностями равных фаз, поэтому они, как и волны в среде без потерь, являются однородными волнами (рис.1).
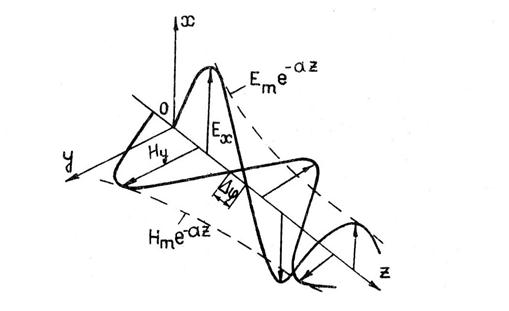
Рис.1
Вектор Пойнтинга и средний за период вектор Пойнтинга будут определятся выражениями
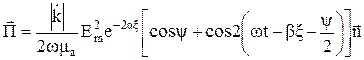 , (13а)
, (13а) 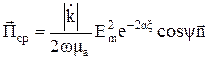 , (13б)
, (13б)
из которых видно, что в среде с потерями вектор Пойнтинга может иметь направление, противоположное направлению распространения волны, в то время как средний за период вектор Пойнтинга всегда совпадает с направлением распространения плоской волны. Ослабление или затухание плотности потока мощности как мгновенного значения П, так и среднего за период П, происходит вдвое быстрее, чем амплитуд составляющих.
Затухание измеряется в децибелах
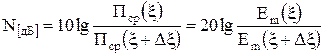 , (14)
, (14)
Подставляя, получим
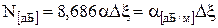 , (15)
, (15)
где 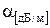 - погонное затухание (затухание на единицу длины в дБ/м).
- погонное затухание (затухание на единицу длины в дБ/м).
Из (5) погонное затухание в дБ/м определяется как
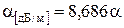 . (16)
. (16)
2. Скорость распространения ЭМВ в различных средах. Дисперсия
Фазовая скорость плоской электромагнитной волны в средах с потерями
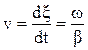 (17)
(17)
определяется коэффициентом фазы и зависит от частоты электромагнитных колебаний. Зависимость фазовой скорости гармонических волн от их частоты называется дисперсией, поэтому в средах с потерями имеет место дисперсия.
Скорость распространения энергии
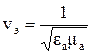 . (18)
. (18)
Таким образом, подтверждается естественный вывод о том, что энергия гармонической волны переносится полем волны и распространяется с фазовой скоростью электромагнитной волны. Этот вывод справедлив для любых однородных изотропных сред.
ГРУППОВАЯ СКОРОСТЬ
В средах с потерями или в других условиях, например, в волноводных линиях передачи, фазовая скорость зависит от частоты электромагнитных колебаний, т.е. имеет место дисперсия. Проходя один и тот же путь, гармонические волны, составляющие единый пакет волн реального сигнала, получают различные фазовые сдвиги, что ведет к искажению формы самого сигнала. Очевидно, чем уже спектр сигнала, тем меньше разница между фазовыми скоростями гармонических составляющих сигнала, тем меньше его искажение.
Для характеристики перемещения энергии какого-либо сигнала, относящегося к узкополосным сигналам, вводят понятие групповой скорости сигнала, понимаемая под этим скорость перемещения максимума огибающей этого сигнала.
В общем случае любой реальный сигнал может быть представлен в виде бесконечной суммы гармонических волн, которую на примере напряженности электрического поля электромагнитной волны сигнала можем записать в виде интеграла Фурье
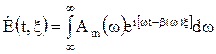 , (19)
, (19)
где  - амплитуда каждой из гармонических волн;
- амплитуда каждой из гармонических волн; 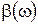 - коэффициент фазы каждой из этих волн.
- коэффициент фазы каждой из этих волн.
Если спектр сигнала достаточно узкий (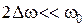 ), т.е. заключен в интервале частот -
), т.е. заключен в интервале частот -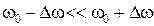 , где w0 - центральная частота спектра сигнала,
, где w0 - центральная частота спектра сигнала, 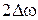 - активная ширина спектра сигнала, то вне этого интервала
- активная ширина спектра сигнала, то вне этого интервала 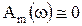 , поэтому (18) представим в виде
, поэтому (18) представим в виде
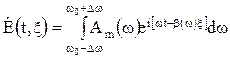 , (20)
, (20)
Коэффициент фазы можно представить рядом Тейлора в окрестности w0
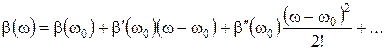 (21)
(21)
и для узкополосного сигнала ограничиться лишь первыми двумя членами. Это позволяет перейти к новой переменной 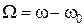 для рассмотрения сигнала в пределах спектра и получить
для рассмотрения сигнала в пределах спектра и получить
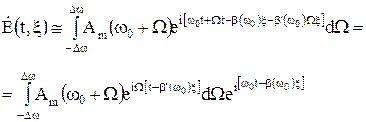 . (22)
. (22)
Теперь (22) можем представить в виде
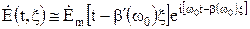 , (23)
, (23)
из которого видно, что аргумент - 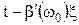 амплитудного множителя
амплитудного множителя 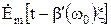 отличается от аргумента, определяющего распространение центральной части спектра. Именно аргумент амплитудного множителя характеризует распространение всех составляющих спектра в целом, т.е. распространение пакета (группы) волн сигнала, его энергии.
отличается от аргумента, определяющего распространение центральной части спектра. Именно аргумент амплитудного множителя характеризует распространение всех составляющих спектра в целом, т.е. распространение пакета (группы) волн сигнала, его энергии.
При 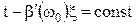 с непрерывно меняющимся временем пакет волн будет перемещаться в пространстве со скоростью
с непрерывно меняющимся временем пакет волн будет перемещаться в пространстве со скоростью
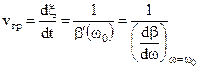 , (24)
, (24)
называемой групповой скоростью или скоростью распространения энергии сигнала. Индекс w=w0 в (24) можно опустить ввиду произвольности выбора центральной частоты.
Условием применимости (24) является малая скорость изменения коэффициента фазы вблизи частоты и узость спектра сигнала, так как в разложении (21) отброшены члены порядка выше первого. При невыполнении этих условий влияние дисперсии становится весьма заметным и сигнал в процессе распространения так сильно меняет свою форму, что само понятие групповой скорости теряет смысл.
В средах без потерь 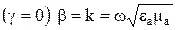 , поэтому групповая скорость совпадает с фазовой
, поэтому групповая скорость совпадает с фазовой
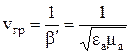 . (25)
. (25)
В средах с потерями фазовая и групповая скорости не совпадают, но связаны между собой (рис.2). Для установки этой связи продифференцируем выражение (17) по частоте
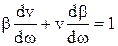 , (26)
, (26)
из которого получим
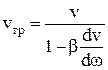 . (27)
. (27)
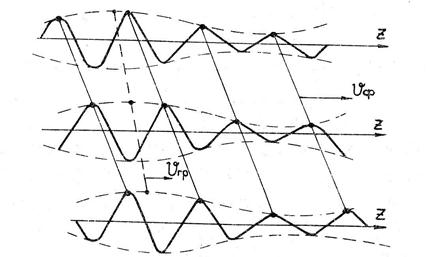
Рис.2
Соотношение (27) показывает, что в средах с аномальной дисперсией 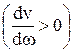 , к которым относятся однородные изотропные среды с потерями, групповая скорость больше фазовой, в то время как в средах или в условиях с нормальной дисперсией
, к которым относятся однородные изотропные среды с потерями, групповая скорость больше фазовой, в то время как в средах или в условиях с нормальной дисперсией 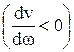 она меньше фазовой скорости электромагнитных колебаний в них.
она меньше фазовой скорости электромагнитных колебаний в них.
3. ПОВЕРХНОСТНЫИ ЭФФЕКТ
Явление концентрации электромагнитного поля и вызванного им высокочастотного тока у поверхности проводника получило название поверхностного эффекта.
Полезным проявлением этого эффекта является возможность применения проводников для экранирования различных радиоустройств и защиты человека от электромагнитных излучений. Однако поверхностный эффект приводит к возрастанию активного сопротивления проводника при протекании высокочастотного тока в нем.
При этом речь ведут о глубине проникновения d ЭМВ в материал, который определяется как глубина проводника, на которой уровень напряженности поля уменьшается в е раз от исходного, тогда
d=1/a. (28)
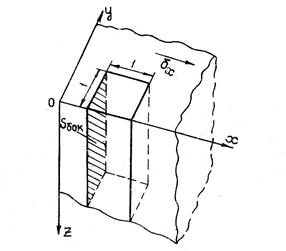 Рассмотрим явление поверхностного эффекта и учет его на примере шлифа проводника с размерами и, во много раз меньшими длины волны, падающей на поверхность шлифа (рис.3).
Рассмотрим явление поверхностного эффекта и учет его на примере шлифа проводника с размерами и, во много раз меньшими длины волны, падающей на поверхность шлифа (рис.3).
Под действием электрического поля волны в проводнике протекает ток проводимости, причем амплитуда его плотности и амплитуда электрического поля волны убывает по экспоненциальному закону с увеличением расстояния вглубь проводника, в котором 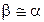 :
:
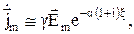 (29)
(29)
где Еm - амплитуда поля на поверхности Рис.3 шлифа.
Теоретически поле плоской электромагнитной волны проникает в проводник на бесконечно большое расстояние, поэтому комплексная амплитуда тока проводимости, вызванного электромагнитной волной в проводнике и определяемого как поток плотности тока через поверхность 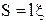 ,
,
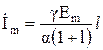 . (30)
. (30)
Ток 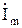 (23) можно считать током, вызванным высокочастотным напряжением с известной амплитудой
(23) можно считать током, вызванным высокочастотным напряжением с известной амплитудой 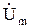 на поверхности
на поверхности 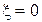 .
.
Поверхностное сопротивление
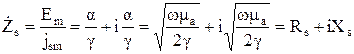 , (31)
, (31)
Понятие поверхностного сопротивления определяет волновое сопротивление электромагнитной волны в проводящей среде. Поверхностное сопротивление (31), а значит и сопротивление проводника, является активно-индуктивным, поэтому потери энергии на нагрев проводника определяются его активной частью
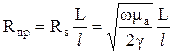 . (32)
. (32)
Очевидно, что сравнивать потери в проводнике при протекании в нем токов высокой частоты и постоянного тока можно только по величинам погонных сопротивлений для высокочастотных токов и постоянного тока.
Погонное сопротивление постоянному току определяется
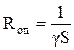 , (33)
, (33)
в которой применительно к рис.3. неизвестна только площадь поперечного сечения 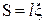 из-за неопределенности расстояния. Но эта неопределенность легко устраняется, если ограничиться слоем
из-за неопределенности расстояния. Но эта неопределенность легко устраняется, если ограничиться слоем 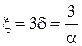 , в котором концентрируется 99% энергии волны в проводнике, поэтому
, в котором концентрируется 99% энергии волны в проводнике, поэтому
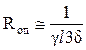 . (34)
. (34)
В то же время активное погонное сопротивление проводника при протекании в нем высокочастотных токов
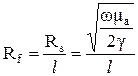 , (35)
, (35)
поэтому 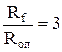 , т.е. погонное сопротивление проводника при высокочастотных токах практически в три раза превосходит погонное сопротивление того же проводника при постоянном токе.
, т.е. погонное сопротивление проводника при высокочастотных токах практически в три раза превосходит погонное сопротивление того же проводника при постоянном токе.
Для уменьшения погонного сопротивления проводников, применяемых для монтажа радиоаппаратуры, используются высоко проводящие металлы, из которых наиболее употребительна медь. Кроме того применяются все меры к увеличению поперечного размера l. Это достигается изготовлением и применением многожильных проводов, нанесением сравнительно широких, но тонких полос проводника на диэлектрическую основу плат.
Вредное воздействие электромагнитного поля оценивается энергией нагрева. Поэтому более вредное воздействие оказывают ЭМП более высоких частот. Для защиты организма от вредного воздействия такого поля применяют специальные экранирующие костюмы из медной проволоки. Необходимо помнить, что энергия ЭМП сильно убывает с расстоянием.
ЗАКЛЮЧЕНИЕ
Таким образом, рассмотрев материал лекции, изучили основные особенности распространения электромагнитных колебаний в средах с потерями. Получили выражения, описывающие скорости распространения ЭМВ в зависимости от электрических параметров среды и возможность использования поверхностного эффекта для экранирования радиоаппаратуры.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1243; Нарушение авторских прав?; Мы поможем в написании вашей работы!