Kinematics – it is a part of mechanics which study a ways of description of motion and bond between quantities of motion

Рhysics is science about the nature

Kinematics of point

A particle at time t moving along a curved path in this plane. Its position or displacement from the origin is measured by the vector; its velocity is indicated by the vector v. The acceleration is indicated by the vector a.

S v

a r

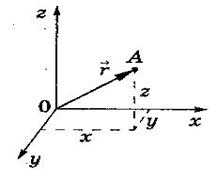
If the particle moves along the x axis from position x₁ to position x₂ its displacement is given by x₁ - x₂ (x₁ –initial and x₂- final values). We use the Greek letter delta (D) to denote the change in a quantity. Therefore, we definite the change in the position of the particle as

Uniform motion on circleit is very simple motion, because |u|= constbut direction changes. The velocity of body in any point of the curvilinear trajectory will direct on tangent to curve in this point At curvilinear motion the acceleration always direct to center of circle An angle in radians q is given by the ratio between the are length S that subtends the angle to the radius of the circle q = S/R φ = 2π, were φ is angle of turning 1 rad = 360^0/ 2π

Centripetal acceleration. As the particle proceeds along its circular orbit, R continually changes its direction even through w may be constant. As a result velocity also changes in direction.

In Fig.1 the velocity vector of such a particle is shown at two nearly points in its path. These vectors have the same magnitude, but their directions differ. The average acceleration which the particle experiences between these points is called the centripetal acceleration a_c = Du/Dt = (u₂ - u₁)/ (t₂ – t₁) The triangles bounded by R₁DR R₂, and by u₁Duu₂ are similar to one another, since R₁ ^u₂, R₂ ^u₁ Then Du/u = DR/R or Du = uDR/R DR = s, then Du = us/R a_c = Du/Dt a_c = us/R Dt s/Dt = u a_c = u²/R  

Fig 1. Computing centripetal acceleration.

Let’s the centripetal acceleration characterize across r and T – period of rotation and frequency n. The linear velocity equal to: u = 2 πR/T The angular velocity w it is ratio of the angle of turning Dφ to time interval Dt w = Dφ / Dt If at time t=T the body perfects one turning and Dφ=2π, then w = 2π/T The unit of the angular velocity is rad/s n = 1/T, then w = 2πn Most of experienced waves as children when we dropped a pebble into a pond. The disturbance created by the pebble excites ripple waves, which move outward, finally reaching the chore of the pond. The water wave (or disturbance) moves from one place to another, yet the water is not carried with it. Water waves represent only one example of a wide variety of physical phenomena that have wavelike characteristics. The world is full of waves: sound waves; mechanical waves, such as a wave on a string; earthquake waves; shock waves generated by supersonic aircraft; electromagnetic waves, such as visible light, radio waves, television signals and x-rays. Three physical characteristics are important in characterizing waves: the wavelength, the frequency and the wave velocity. One wavelength is the distance between any two pints on a wave that behave identically. For example, in the case of water waves, the wavelength is the distance between adjacent crests or between adjacent troughs. Most waves are periodic in nature. The frequency of such periodic waves is the rate at which the disturbance repeats itself. Wave travel or propagate, with a specific velocity, which depends on the properties of the medium being disturbed The shape of the harmonic wave is a sinusoidal curve, as shown in fig. 1. 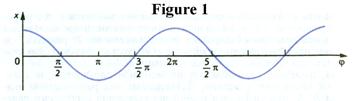  The constant A called the amplitude of the wave, represents the maximum value of the displacement. The constant l called the wavelength of the wave, equals the distance between two successive maxima, which we shall refer to as crests, or between any two adjacent points that have the same phase. The time it takes the wave to travel a distance of one wavelength is called the period, T. 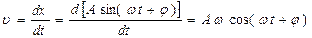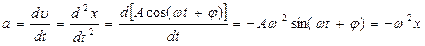Therefore, the phase velocity, wavelength and period are related by u = l/T or l = u/T Definition of amplitude and beginning conditions of harmonic waves Representation of harmonic vibration with the help of sine and cosine x = x_m sin (w₀t+φ₀) or x’ = w₀x_m cos (w₀t+φ₀) or at t=0 x₀ = x_m sin φ₀ Velocity of oscillations is _{acceleration is} Phase of oscillation At a given amplitude of harmonic vibration the coordinate of body at any moment of time is determined by the argument of cosine and sine φ = ω_ot. φ = (w₀t+φ₀) – is phase If time t =0, then φ = φ₀. In this case the means of the phase called initial phase and x = x_m sin w₀t or x = x_m cos w₀t If ω_o = 2π/T, then φ = ω_ot = 2πt/T. The relation t/T indicates what parts of period passed from moment of begin vibration. Any value of time expressed in portions [shares] of period corresponds to the value of phase expressed in radian Dictionary

disturbance	Беспокойство, волнение, нарушение порядка	Ретсіздік
excites	Вызывать интерес, возвуждать	қоздыру
ripple	журчание	сыңғырлау
earthquake	Землетресение	Жер сілкініс
adjacent	Смежный,соседний	іргелес
troughs	Подошва волны	Тоқын етегі
crests	Гребень волны, максимум	Толқын айдары
harmonic vibration	Гармонические колебания	Гармоникалық тербелістер
Frequency	частота	жиілік
amplitude	амплитуда	амплитуда
Beginning conditions	Начальные условия	Бастапқы шарттар
Free oscillations	свободные колебания	Еркін тербелістер
Forced oscillations	вынужденные колебания	Еріксіз тербелістер
phase of oscillation	фаза колебаний	Тербелістер фазасы
radian	радиан	радиан

English

Russian

Kazakh

Description

oписывать

сүреттеу

magnitude

величина, важность

мән, маңызды

path

обрывок, кусок. учсаток

қиқым

distinctly

определнный, ясный

нақты, белгіленген

proof

проверка

тексеру

Space

пространство

кеңістік

Straightforward

прямолинейное

тік сызықты

uniform

равномерное

біртекті

circle

окружность

шеңбер

curvilinear

криволтнейное

қысықсызықты

angle of turning

угол поворота

айналу бұрышы

Centripetal

центростремительное

центрге тартқыш

acceleration

ускорение

үдеу

perfects

совершать

жасау

Оның қозғалысының дифференциал теңдеуі

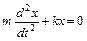
Нүктенің толық энергиясы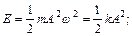

Пружинді маятник тербелісінің периоды 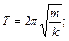m- дене массасы; к-пружинаның қатаңдығы

Математикалық маятниктің тербеліс периоды

-маятник ұзындығы

g- еркін түсу үдеуі

Математикалық маятник деп- ұзын жіпке ілінген кішкентай денені айтады.

Физикалық маятниктің тербеліс периоды ;

J- тербелмелі оське қатысты дененің инерция моменті;

а-тербелмелі осьтен маятник центіріне дейінгі қашықтық

физикалық маятниктің келтірілген ұзындығы.

Физикалық маятник деп, горизонталь оське бекітілген және өзінің масса центірінен өтпейтін оське қатысты тербелістегі денені айтады

Дата добавления: 2013-12-13