Логическая сумма и логическое произведение

Классификация

Классификация является разновидностью деления понятия, представляет собой вид последовательного деления и образует развернутую систему, в которой каждый ее член (вид) делится на подвиды и т. д. Классификация сохраняется весьма длитель­ное время, если она имеет научный характер. Например, посто­янно уточняется и дополняется классификация элементарных частиц. От обычного деления классификация отличается относи­тельно устойчивым характером. Вот три примера классифика­ции: “В организме животных и человека существуют четыре груп­пы тканей: покровная, соединительная, мышечная и нервная. Организм высших растений построен из пяти основных типов тка­ней: образовательной, покровной, основной, механической и про­водящей”; “Простейшие подразделяются на четыре группы (клас­са): жгутиковые, корненожки, споровики, инфузории”'.

Чтобы классификация была правильной, необходимо выпол­нять все правила операции деления.

Существуют классификация по видообразующему призна­ку и дихотомическая классификация. Вышеприведенные три примера представляют классификацию по видообразующему при­знаку. “Зеркала классифицируются на плоские и сферические; сферические зеркала классифицируются на вогнутые и выпуклые” - при­мер дихотомической классификации. Дихотомическое деление всегда правильное, т. е. в нём автоматически исключаются все возможные в делении ошибки, о которых речь пойдёт ниже.

Очень важен выбор основания классификации. Разные основания дают различные классификации одного и того же по­нятия, например, понятия “рефлекс”'.

Классификация может производиться по существенным признакам (естественная) и по несущественным признакам (вспомогательная).

Естественная классификация - это распределение предме­тов по группам (классам) на основании их существенных при­знаков. Зная, к какой группе принадлежит предмет, мы можем судить о его свойствах. Д. И. Менделеев, расположив химичес­кие элементы в зависимости от их атомного веса, вскрыл зако­номерности в их свойствах, создав Периодическую систему элементов, позволившую предсказать свойства не открытых еще химических элементов.

Естественная классификация животных охватывает до 1,5 млн. видов, а классификация растений включает около 500 тыс. Однако каждая классификация относительна, приблизительна, ибо суще­ствуют переходные формы. Иногда переходная форма составляет самостоятельную группу (вид). Например, при классификации наук возникают такие переходные формы, как биохимия, геохимия, фи­зическая химия, космическая медицина, астрофизика и др. Пере­ходные случаи мы встретим и при классификации частей речи.

Существует несколько логических правил деления. Нарушение хотя бы одного из них приводит к тому, что объём понятия не раскрывается и деление не достигает своей цели, являясь неверным. Рассмотрим эти правила и ошибки, возникающие при их нарушении:

1. Деление должно проводиться по одному основанию, т. е. при делении понятия следует придерживаться только одного выбранного признака. Например, в делении: «Люди бывают мужчинами, женщинами и учителями», – используются два разных основания: пол и профессия, что недопустимо. Ошибка, возникающая при нарушении этого правила, называется подменой основания.

В делении с подменой основания могут использоваться не только два разных основания, как в приведённом выше примере, но и больше. Например, в делении: «Люди бывают мужчинами, женщинами, китайцами и блондинами», – использованы три разных основания: пол, национальность и цвет волос, что, конечно же, тоже является ошибкой.

2. Деление должно быть полным, т. е. надо перечислить все возможные результаты деления: суммарный объём всех результатов деления должен быть равен объёму исходного делимого понятия.

Например, деление: «Учебные заведения бывают начальными и средними», – является неполным, т. к. не указан ещё один результат деления – «высшие учебные заведения». Но как быть, если надо перечислять не два или три, а десятки или сотни результатов деления.

В этом случае можно употреблять следующие понятия: и другие, и прочие, и так далее, и тому подобное, которые будут включать в себя не перечисленные результаты деления. Например: «Люди бывают русскими, немцами, китайцами, японцами и представителями других национальностей».

3. Результаты деления не должны пересекаться, т. е. понятия, представляющие собой результаты деления, должны быть несовместимыми, их объёмы не должны иметь общих элементов (на схеме Эйлера круги, обозначающие результаты деления, не должны соприкасаться). Например, в делении: «Страны мира делятся на северные, южные, восточные и западные», допущена ошибка – пересечение результатов деления. На первый взгляд, приведённое деление кажется безошибочным: оно проведено по одному основанию (сторона света) и является полным (все стороны света перечислены). Чтобы увидеть ошибку, надо рассуждать так. Возьмём какую-нибудь страну, например Канаду, и ответим на вопрос, является ли она северной. Конечно, является, т. к. расположена в северном полушарии Земли. А является ли Канада западной страной?

Да, потому что она расположена в западном полушарии. Таким образом, получается, что Канада – одновременно и северная, и западная страна, т. е. она является общим элементом объёмов понятий «северные страны» (С) и «западные страны» (З), а значит, эти понятия пересекаются. То же самое можно сказать и относительно понятий «южные страны» (Ю) и «восточные страны» (В). На схеме Эйлера результаты деления из нашего примера будут располагаться так (рис. 15):

Вспомним, каждая классификация построена таким образом, что любой элемент, попадающий в одну её группу (часть, вид), ни в коем случае не попадает в другие. Это и есть следствие непересечения результатов деления (их взаимоисключения).

4. Деление должно быть последовательным, т. е. не допускающим пропусков и скачков. Рассмотрим следующее деление: «Леса бывают хвойными, лиственными, смешанными и сосновыми». Явно лишним здесь выглядит понятие «сосновые леса», в силу чего допущенная в делении ошибка напоминает подмену основания (см. первое правило). Однако основание в данном случае не менялось: деление было проведено по одному и тому же основанию – тип древесных листьев. Подмена основания присутствует в таком, например, делении: «Леса бывают хвойными, лиственными, смешанными, подмосковными и таёжными». Деление проведено по двум разным основаниям: тип древесных листьев и географическое местонахождение леса. Вернёмся к нашему первому примеру. Правильно было бы разделить леса на хвойные, лиственные и смешанные, а потом произвести второе деление – разделить хвойные леса на сосновые и еловые. Таким образом, надо было совершить два последовательных деления, а в приведённом примере второе деление пропущено, через него как бы перескочили, в результате чего два деления смешались в одно. Такая ошибка называется скачком в делении. Ещё раз отметим, что скачок в делении не следует путать с подменой основания. Например, в делении: «Учебные заведения бывают начальными, средними, высшими и университетами», – присутствует скачок, а в делении: «Учебные заведения бывают начальными, средними, высшими и коммерческими», – допущена подмена основания.

Проверьте себя:

1. Что такое деление понятия?

2. Какова структура деления? Что такое основание деления?

3. Какое деление называется дихотомическим? Попробуйте отметить достоинства и недостатки дихотомического деления.

4. Какую роль в научном и повседневном мышлении играет логическая операция деления понятия?

5. Каковы основные логические правила деления понятия? Какие ошибки возникают при их нарушении? Придумайте по три примера для каждой ошибки в делении понятия.

6. Почему дихотомическое деление понятия всегда безошибочно?

Каким образом оно исключает все возможные в делении ошибки?

7. Найдите ошибки в приведённых ниже примерах деления:

1) Транспорт бывает наземным, подземным, водным, воздушным, общественным и личным.

2) По темпераменту люди делятся на сангвиников, меланхоликов, флегматиков и холериков.

3) Геометрические фигуры делятся на плоские, объёмные, треугольники и квадраты.

4) Отбор в живой природе бывает искусственным или естественным.

5) Художественные романы бывают приключенческими, детективными, фантастическими, историческими, любовными и другими.

Сложение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объёмом, охватывающим собой все элементы объёмов исходных понятий. Например, при сложении понятий «школьник» (Ш) и «спортсмен» (С) образуется новое понятие, в объём которого входят как все школьники, так и все спортсмены. Результат сложения понятий, часто называемый логической суммой, на схеме Эйлера изображается штриховкой (рис. 16).

Умножение понятий – это логическая операция объединения двух и более понятий, в результате которой образуется новое понятие с объёмом, охватывающим собой только совпадающие элементы объёмов исходных понятий. Например, при умножении понятий «школьник» (Ш) и «спортсмен» (С) образуется новое понятие, в объём которого входят только школьники, являющиеся спортсменами, и спортсмены, являющиеся школьниками. Результат умножения понятий, часто называемый логическим произведением, на схеме Эйлера изображается штриховкой (так же, как и результат сложения) (рис. 17).

Мы привели примеры сложения и умножения понятий, которые находятся между собой в отношении пересечения: «школьник» и «спортсмен».

При других отношениях между понятиями результаты сложения и умножения (логическая сумма и логическое произведение), разумеется, будут иными. В приводимой ниже табл. 3 штриховкой показаны результаты сложения и умножения понятий во всех видах отношений между ними.

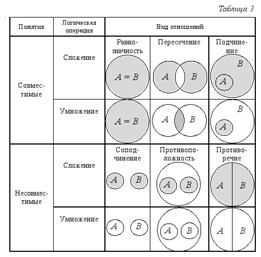
Результаты сложения понятий во всей первой строке табл. 3 (в равнозначности, пересечении и подчинении) полностью совпадают с результатами сложения во всей третьей строке табл. 3 (в соподчинении, противоположности и противоречии). А результаты умножения понятий во всей второй строке табл. 3 (в равнозначности, пересечении и подчинении), наоборот, полностью не совпадают с результатами умножения во всей четвёртой строке табл. 3 (в соподчинении, противоположности и противоречии).

Кроме того, результаты сложения понятий, при сравнении их с результатами умножения, полностью совпадают только в случае равнозначности, частично – в пересечении и совершенно не совпадают в соподчинении, противоположности и противоречии (в этих трёх случаях результатом умножения является нулевое или пустое понятие). В отношении подчинения результатом сложения является родовое понятие, а умножения – видовое.

Как правило, в естественном языке (том, на котором мы общаемся) результат сложения понятий выражается союзом «или», а умножения – союзом «и». В результате сложения понятий «школьник» и «спортсмен» образуется новое понятие, в объём которого входит любой человек, если он является или школьником, или спортсменом, а в результате умножения этих понятий в объём нового понятия входит любой человек, если он является и школьником, и спортсменом одновременно.

О возможных разночтениях при употреблении союзов «или » и «и » говорит Виталий Иванович Свинцов в уже упоминавшемся нами учебнике по логике: «Что касается союзов «или» и «и», то нужно отметить их многозначность, способную в известных ситуациях создавать достаточно неопределённое представление о характере связи между некоторыми исходными понятиями. Удачна ли, например, следующая формулировка одного из правил пользования городским транспортом: «Безбилетный проезд и бесплатный провоз багажа наказывается штрафом»? Представим себе два подмножества, которые могут быть выделены во множестве пассажиров-нарушителей. В одно из них войдут пассажиры, не взявшие билета, в другое – не оплатившие провоз багажа. Если союз «и» рассматривать как показатель логического умножения, то придётся признать, что штраф должен быть наложен только на тех пассажиров, которые совершили сразу два проступка (но не какой-то один из них). Разумеется, житейский смысл ситуации, предусмотренной данным правилом, настолько ясен, что всякие разночтения этой формулировки, вероятно, были бы признаны казуистикой, но всё же использование союза «или» здесь следует признать предпочтительным»^[3].

Проверьте себя:

1. Что такое логическая сумма и логическое произведение?

2. Возьмите три пары каких-нибудь понятий и проделайте с ними логические операции сложения и умножения, иллюстрируя их результаты с помощью круговых схем Эйлера.

3. Каковы результаты сложения и умножения понятий во всех случаях отношений между ними? Могут ли эти результаты полностью совпадать? Может ли логическая сумма или логическое произведение быть нулевым понятием?

4. Какой союз естественного языка является, как правило, выражением результата сложения понятий, какой – умножения? Проиллюстрируйте свой ответ самостоятельно подобранными примерами.

О РОЛИ ИМЕН

Слова, как и люди, могут играть разные роли. Смешение ролей, или употреблений, одного и того же слова может оказаться причиной его неясности и непонимания. На это обратили внимание еще средневековые логики, использовавшие термин "суппозиция" для обозначения разных употреблений имени.

В обычном языке одно и то же имя может относиться к предметам разных типов. В общем случае имя – это выражение языка, обозначающее отдельный предмет, совокупность сходных предметов, свойства, отношения и т.п.

Во-первых, оно может использоваться для обозначения любого отдельного предмета соответствующего класса. Употребление имени в его собственном, или обычном, смысле для обозначения произвольного объекта своего объема называется формальным (или естественным) употреблением. Например, слово, "дерево" обычно является общим именем множества деревьев. Говоря, "Дерево – это растение", мы имеем в виду: "Каждое дерево – растение".

Во-вторых, имя может обозначать себя, т.е. использоваться в качестве своего собственного имени. Примерами такого употребления имени "человек" могут служить утверждения: ""Человек" начинается с согласной буквы", ""Человек" состоит из трех слогов", ""Человек" – существительное с неправильным множественным числом". Употребление имени в качестве обозначения самого себя называется материальным употреблением.

В-третьих, имя, когда оно используется в определенном контексте, может оказаться именем единичного объекта того класса объектов, который обычно обозначается этим именем. Так, слово "человек" обозначает множество людей, но в конкретном случае оно может употребляться для обозначения отдельного человека: мы говорим "Идет человек", подразумевая: "Идет конкретный человек". Употребление общего имени для обозначения отдельного, конкретного объекта из числа всех входящих в его объем объектов называется персональным употреблением.

В-четвертых, при так называемом простом употреблении имя используется для обозначения всего соответствующего класса объектов, взятого как целое. Слово "человек" обозначает при таком употреблении всех людей, рассматриваемых как некоторое единство: "Человек является одним из видов живых существ", "Человек со временем посетит все планеты Солнечной системы" и т.п.

Изучение употреблений имен важно для предотвращения логических ошибок.

– Знаешь, – говорит один мальчик другому, – я умею говорить по-китайски, по-японски и по-арабски. – Не может быть. – Если не веришь, давай поспорим. – Давай поспорим. Ну, начинай говорить по-китайски. – Пожалуйста: "по-китайски", "по-китайски"... Хватит? – Ничего не понимаю. – Еще бы, я ведь говорю "по-китайски". А ты проиграл спор. Если хочешь, я буду говорить "по-арабски"...

В этом диалоге один из мальчиков использует имя "по-китайски" в его материальном употреблении, т.е. как имя этого же самого слова. Он обещает произносить слово, обозначаемое данным именем и совпадающее с ним. Второй мальчик имеет в виду естественное употребление слова "по-китайски" и ожидает разговора на китайском языке. Очевидно, что затеянный ими спор неразрешим. Спорившие говорили о разных вещах: один – в своей способности повторять без конца слово "по-китайски", а другой – о разговоре на китайском языке.

В рассуждении "Поскольку человек – вид живых существ, а столяр – человек, то столяр – вид живых существ" явно смешиваются простое и формальное употребления имени "человек".

В современной логике из многочисленных употреблений имен, выделявшихся средневековыми логиками, сохранило свое значение различение формального и материального употреблений. Все остальные употребления слишком неопределенны и неустойчивы, чтобы ими пользоваться. При построении искусственных (формализованных) языков логики, от которых требуется однозначность, употребление одного и того же имени в разных "ролях" способно привести к неопределенности и ошибкам.

Использование имени или иного выражения в материальном употреблении, т.е. в качестве имени самого себя, получило название автонимного употребления выражений. Оно широко распространено в логике и математике. Сохранение в одном языке двух "ролей" одних и тех же слов – их формального и материального употреблений – двусмысленно. Но эта двусмысленность часто бывает удобной. Например, вместо того, чтобы писать слова "знак сложения", мы можем писать "+", и этот крестик является именем самого себя.

В обычном языке возможность разных употреблений одних и тех же имен сохраняется. Однако не всегда ясно, какое именно употребление, скажем, имени "человек" имеется в виду в выражениях типа "Человек – это звучит гордо", "Человек человеку всегда придет на помощь" и т.п.

Двусмысленностей и непонимания, связанных с путаницей между естественным употреблением имени и его употреблением как своего собственного имени, можно всегда избежать. Для этого используются либо дополнительные слова в формулировке утверждения, либо кавычки, либо курсив. Скажем, кто-то может написать: "Человек состоит из трех слогов". Но чтобы не возникло недоразумения, надо употребить какую-либо из следующих форм: "Слово "человек" состоит из трех слогов". ""Человек" состоит из трех слогов" или " Человек состоит из трех слогов".

Дата добавления: 2013-12-13