Уравновешенные системы счисления

Способы выполнения операции округления числа в позиционных СС. Погрешность округления. Округление числа в ЭВМ. Простейшая процедура округления с наименьшей ошибкой. Уравновешенные системы счисления.

Округление числа в позиционных системах счисления. Поскольку все числа в ЭВМ записываются в конечную разрядную сетку, очень актуальна процедура округления числа до требуемого количества разрядов.

Округлением числа x до s разрядов в заданной системе счисления называется операция замены его таким числом x_s, все разряды которого, начиная с (s – 1) -го и младше, равны нулю.

Простейшая процедура округления заключается в "отбрасывании" разрядов, начиная с (s – 1)-го. Таким образом, если число x имеет вид

то

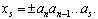
Разность между округлённым и округляемым значениями называется ошибкой (погрешностью) округления:

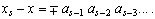
Очевидно, что при таком способе округления (назовём его первым) ошибка всегда будет иметь знак, противоположный знаку округляемого числа. Это может приводить к быстрому накоплению ошибки в вычислениях.

Давайте оценим ошибку по величине. Абсолютная погрешность округления 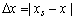имеет наибольшее значение, когда числа 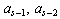и т. д. принимают наибольшее значение, равное максимальному базисному числу в рассматриваемой системе счисления с основанием p:

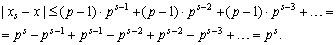
Итак, верхняя оценка для абсолютной погрешности получилась равной

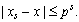
Сравним её с погрешностью общепринятого (второго) способа округления в 10-ичной СС. Для этого рассмотрим таблицу 1 0.1.

Таблица 10.1

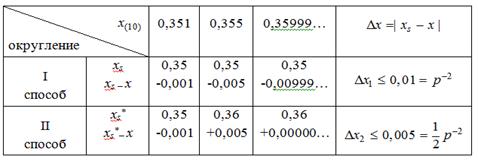
Из таблицы видно, что наибольшая абсолютная погрешность округления во втором случае равна p^s:

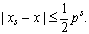
Кроме того, знак ошибки округления будет меняться, т.к. в половине случаев округление идет с недостатком, а в половине - с избытком. Поэтому накопление ошибки в арифметических действиях не будет происходить заведомо быстро.

Итак, мы видим, что процесс округления, выполняемый по аналогии с принятым в 10-ичной системе счисления, является лучшим, так как он обеспечивает наименьшую погрешность округления.

Выразим данную процедуру округления формально. Числа, имеющие нулевые разряды, начиная с (s – 1)-го, образуют на вещественной оси равномерную сетку с шагом p^s. Среди них есть число 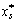, наиболее близкое к x. Ясно, что

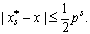
Из геометрических соображений следует, что наилучшее приближение 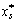к x будет единственным, если имеет место строгое неравенство. Учитывая возможность равенства, запишем

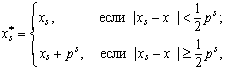(10.1)

где x_s – округление отбрасыванием разрядов;

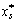– наилучшее округление;

p^s – единица s –го разряда.

Этот способ округления идентичен принятому в 10-ичной системе счисления. В машинах он реализуется в два этапа: 1) к старшему из отбрасываемых разрядов, (s – 1)-му, прибавляем p^s; 2) разряды с (s – 1)-го отбрасываются.

Округление числа до верной цифры. Числа, представляющие собой результат вычислений или измерений, как правило, содержат ошибку и в общем случае их принято записывать в виде

,

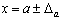где 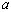– приближенное значение числа x;

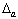– абсолютная погрешность этого приближения.

В соответствии с требованиями теории погрешностей все цифры числа 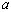должны быть верными. Приведем определение.

Цифра a_i в записи p -ичной дроби приближенного числа a называется верной, если погрешность приближения не превышает единицы i -го разряда.

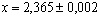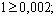
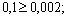
Например, рассмотрим запись . Цифры 2, 3, 6 являются верными, так как выполняются неравенства 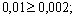а цифра 5 является сомнительной, поскольку единица разряда, в котором она записана, меньше погрешности .

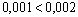В подобных случаях требуется округление числа a до верной s -й цифры a_s. При этом ошибка округления суммируется с исходной абсолютной погрешностью числа 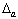. Пусть, начиная с (s – 1)-го разряда, все цифры числа a являются сомнительными. Обозначим сомнительную часть числа . Тогда алгоритм округления до верной s -й цифры имеет вид

где 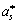– это число a, округленное в соответствии с (10.1).

Так, рассмотренное нами число 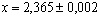после процедуры округления его до верной цифры правильнее будет записать как .

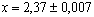Уравновешенные системы счисления. Зададимся вопросом: можно ли добиться того, чтобы достоинства рассмотренных нами двух способов округления присутствовали? Чтобы процедура округления была проста как в первом случае, а погрешность округления мала, как во втором? Оказывается, можно – путём использования систем счисления с соответствующим выбором базисных чисел.

Требуется, чтобы погрешность округления была

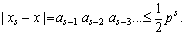
Это означает, что все числа вида 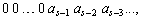являющиеся отбрасываемой частью числа, в искомой системе счисления не должны превосходить по модулю p^s. Для выполнения этого условия, в свою очередь, необходимо и достаточно, чтобы имело место неравенство

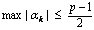(10.2)

для всех k от 0 до p – 1, где α _k – базисные числа искомой СС.

Неравенство (10.2) имеет p целых различных решений только при условии, что p – нечётное. Тогда решения имеют вид

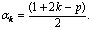
Вычислим их:

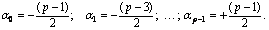
Таким образом, чтобы округление по простейшему способу давало наименьшую ошибку, необходимо, чтобы система счисления имела нечётное основание и базисные числа, расположенные симметрично относительно нуля:

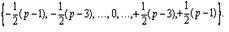
Такие системы счисления называются уравновешенными. Рассмотрим простейшую из них – троичную.

Троичная уравновешенная система счисления

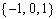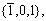Дано основание p = 3, базисные числа образуют совокупность или где 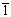означает минус 1. Рассмотрим значение следующих чисел в данной и в 10-ичной системах счисления:

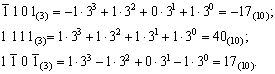
Видно, что знак числа совпадает со знаком первой цифры числа. Это означает, что не требуется указывать отдельно знак числа. Кроме того, важным достоинством является простота получения числа, противоположного данному по значению (см. первое и третье числа, равные – 17 и 17 в 10-ичном представлении). Для этого достаточно все цифры «1» заменить на «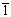» и наоборот в записи числа. Это, как мы далее убедимся, значительно упрощает выполнение операции вычитания, которое есть сложение с числом, противоположным вычитаемому.

Арифметические действия над числами в троичной уравновешенной системе счисления можно задать с помощью таблиц.

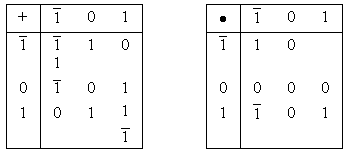
В 1958 году в Советском Союзе была построена экспериментальная модель ЭВМ, арифметика которой базировалась на правилах, приведённых в таблицах, и обладала следующими преимуществами по сравнению с двоичной:

– простота операции округления при наименьшей ошибке;

– знак числа не требует отдельного представления, поскольку совпадает со знаком первой значащей цифры в записи числа;

– простота операции вычитания, поскольку легко получить число, обратное по значению.

Дальнейшего развития идея использования такой СС не получила, хотя в целом вопрос о предпочтительности двоичной или троичной уравновешенной систем счисления по совокупности показателей до сих пор является дискуссионным.

Дата добавления: 2013-12-13