Исследование кулачковых механизмов методом замены высшей КП низшими парами

Кинематическое исследование кулачковых механизмов

Кулачковым называется механизм, в составе которого кроме низших кинематических пар входят и высшие кинематические пары.

Синтез кулачковых механизмов

Кинематический анализ кулачковых механизмов.

ЛЕКЦИЯ 11

Тема: АНАЛИЗ И СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ

Кулачковые механизмы нашли широкое применение в технике (газораспределительные механизмы, командо-аппараты и т.д.) благодаря своей простоте (всего 2-3 звена) и возможностью выполнить практически любой закон движения.

Рассмотрим несколько методов исследования кулачковых механизмов.

Вначале рассмотрим специальный кулачковый механизм, в котором звенья, связанные с элементами высшей КП представляют собой правильные круги (основной случай). Степень подвижности этого механизма

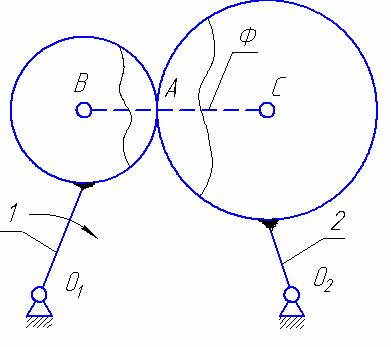W = 3_n - 2P₅ - P₄ = 3 · 2 - 2 · 2 - 1 = 1

Если двигать первое звено, второе также будет двигаться, но расстояние между центрами кругов В и С в любом случае будет постоянно. Следовательно, если образовать в точках В и С вращательные кинематические пары и соединить их звеном, то оно мешать движению не будет. Это условное звено обычно называют фиктивным звеном. Если выбросить части звеньев в окрестности КП А (на рисунке ограничено плавными тонкими линиями), то, с учетом фиктивного звена, движение первого и второго звена не изменится.

Что мы сделали? Мы образовали вращательные КП в центрах окружностей. Один элемент каждой пары соединили с фиктивным звеном, а второй элемент этих вращательных пар соединили со звеном, в центре кривизны которого образовали КП. Полученный механизм называется заменяющим.

W = 3_n - 2P₅ - P₄ = 3 · 3 - 2 · 4 = 1

Его степень подвижности не изменилась и в кинематическом смысле он эквивалентен действительному механизму.

Рассмотрим механизм с произвольной высшей КП (общий случай).

Любую кривую в какой-то точке можно заменить другой кривой с разной степенью точности. Если касательной в точке, то ошибка будет первого порядка. Если кругом кривизны, то ошибка будет третьего и более высоких порядков малости. Следовательно, кривая окружности в точке касания эквивалентна самой кривой до производных второго порядка включительно. И этой ошибкой можно пренебречь.

Таким образом, заменяющий механизм будет эквивалентен в кинематическом смысле механизму с высшими парами до производных второго порядка включительно.

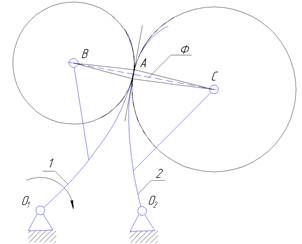
Как построить эти круги? Для этого необходимо найти центры кривизны звеньев в точке контакта любым методом (в данном случае определены методом хорд), которые и будут являться центрами кругов. Далее все делается, как и в основном случае.

Полученный заменяющий механизм будет эквивалентен только для данного положения действительного механизма, так как в общем случае длина фиктивного звена, как и первого и второго звена будут изменяться. Теперь можно проводить кинематическое исследование шарнирно-рычажного механизма известными методами.

Частные случаи замены высшей пары на низшие рассмотрены в литературе [1, 2, …].

1.2. Метод кинематических диаграмм.

Рассмотрим конкретный кулачковый механизм.

Ведущее звено кулачкового механизма, имеющее криволинейный контур называется кулачком (1). Сопряженное с ним звено называется толкателем (2). Толкатели могут двигаться поступательно или качаться относительно неподвижной точки.

Дата добавления: 2013-12-13