Коллоидных систем

Молекулярно-кинетические и оптические свойства

Броуновское движение.

Молекулярно – кинетические свойства коллоидных систем, как и обычных растворов, обнаруживаются в таких явлениях как броуновское движение, диффузия, осмотическое давление. Частицы коллоидных систем (золей, аэрозолей) участвуют в тепловом движении и подчиняются всем молекулярно-кинетическим законам

Броуновское движение проявляется в хаотическом и непрерывном движении частиц дисперсной фазы под действием ударов молекул растворителя (дисперсионной среды), находящихся в состоянии интенсивного молекулярно–теплового движения. В зависимости от размера частиц их движение может принимать различные формы. Траектория движения таких частиц представляет собой ломаную линию совершенно неопределенной конфигурации.

Количественной мерой перемещения частицы при броуновском движении является величина среднего смещения (или сдвига) частицы 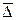за некоторый промежуток времени τ. Смещением или сдвигом частицы называют расстояние между проекциями начальной 1 и конечной 2 точек траектории на ось смещений (на ось x). Смещения одинаково вероятны как слева направо, так и в противоположном направлении. Поэтому при вычислении среднего смещения за большой промежуток времени 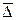может быть равно нулю. В связи с этим вычисляют среднюю квадратичную величину всех смещений без учета направления движения:

,

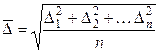где п — число смещений (число отрезков ломаной линии); ∆ _i — отдельные проекции смещения частицы на ось x. А. Эйнштейном и М. Смолуховским было показано, что среднее значение квадрата смещения частицы за время τ равно

,

где D – коэффициент диффузии, t ‑ время.

Эйнштейн нашел, что коэффициент диффузии связан с размерами диффундирующих частиц уравнением

,

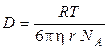где h ‑ вязкость среды, N_A – число Авогадро, r — радиус сферических частиц, размер которых много больше размера молекул растворителя.

Уравнение Эйнштейна для коэффициента диффузии является одним из основных в коллоидной химии, с его помощью можно определить размер частиц коллоидных растворов и молекулярную массу полимеров. Для этого надо лишь экспериментальным путем найти значение коэффициента диффузии D. Для определения величины D необходимо измерить скорость изменения концентрации в слое раствора, в котором происходит диффузия. Концентрацию чаще всего определяют оптическими методами, измеряя показатель преломления, оптическую плотность раствора и т. п.

Из уравнения Эйнштейна-Смолуховского следует, что величина обратно пропорциональна радиусу частицы r. Это означает, что чем крупнее частица, тем меньше величина ее смещения. С увеличением размера частиц прежде всего прекращается поступательное броуновское движение, затем исчезает вращательное движение и остается только колебательное.

Осмотическое давление коллоидных растворов.

Осмос – процесс односторонней диффузии растворителя через полупроницаемую перегородку от раствора с меньшей концентрацией растворенного вещества к раствору с большей концентрацией. Давление, которое нужно приложить в процессе осмоса к раствору, чтобы привести его уровень к уровню чистого растворителя, называют осмотическим давлением.

Осмотическое давление является коллигативным свойством раствора, т. е. его величина определяется числом частиц растворенного вещества (ионов, молекул, атомов, коллоидных частиц и даже более крупных частиц) в единице объёма.

Осмотическое давление разбавленных истинных растворов в соответствии с уравнением Вант – Гоффа равно

,

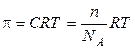где С — молярная концентрация раствора, то есть число моль вещества в 1 л раствора; n – число молекул, атомов или ионов в 1 л раствора; N_A – число Авогадро.

В коллоидных растворах роль отдельной «молекулы» играет коллоидная частица, состоящая из множества молекул. Поэтому для них в уравнении Вант – Гоффа нельзя применять молярную концентрацию в обычном понимании этого термина. Вместо нее мы должны взять частичную концентрацию, которя выражается числом коллоидных частиц в единице объема и обозначается n.

,

где k = R / N_A = 1,38·10^-23 Дж·К^-1 – константа Больцмана.

Из уравнения Вант – Гоффа следует, что осмотическое давление пропорционально числу частиц растворенного или диспергированного вещества в единице объема раствора и не зависит от природы и массы частиц.

Осмотическое давление коллоидных растворов намного меньше, чем для истинных растворов такой же массовой концентрации, так как из–за больших размеров число коллоидных частиц в единице объема намного меньше числа молекул в истинном растворе.

Седиментация в дисперсных системах.

Седиментационно – диффузионное равновесие.

Седиментацией называют процесс оседания частиц дисперсной фазы в жидкой или газообразной среде под действием силы тяжести. Всплывание частиц (например, капель в эмульсиях) носит название обратной седиментации.

Скорость оседания частиц не зависит от их природы, а определяется размером частиц, разностью плотностей частиц ρ и среды ρ₀ и вязкостью среды. Скорость оседания шарообразных частиц с радиусом r равна

,

где g — ускорение силы тяжести.

Если частицы легче среды (например, капли масла в эмульсиях), то разность (ρ – ρ₀) имеет знак минус и, согласно тому же закону, частицы всплывают, а не оседают. Измерив скорость оседания частиц, можно из предыдущего уравнения вычислить радиус частиц. На этом основан седиментационный анализ размеров грубодисперсных частиц в порошках, суспензиях, эмульсиях и взвесях.

Для частиц произвольной формы уравнение для скорости седиментации дает эквивалентный радиус r (радиус сферической частицы, оседающей с той же скоростью). Из уравнения следует, что на скорость оседания частиц можно влиять, изменяя плотность и вязкость среды. Способность к седиментации часто выражают через константу седиментации, величина которой определяется как отношение скорости седиментации кускорению свободного падения g:

.

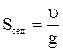Единицей константы седиментации является сведберг (1 Сб = 10^–13 с) или просто секунда. Константа седиментации, как и скорость оседания, зависит от размеров частиц, их плотности и плотности среды, температуры. Величина, обратная константе седиментации, является мерой кинетической устойчивости дисперсной системы:

.

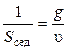Процесс седиментации постепенно приводит дисперсную систему к упорядоченному состоянию, так как оседающие частицы располагаются в соответствии с их размерами (в нижних слоях преобладают крупные, затем более мелкие). Через какой-то промежуток времени все частицы могли бы осесть, как бы малы они ни были. Однако этому противодействуют броуновское движение и диффузия, стремящиеся распределить частицы равномерно по всему объему дисперсионной среды. Между процессами седиментации и диффузии устанавливается равновесие, характеризуемое неоднородным распределением частиц по высоте столба суспензии. Мелкие частицы сильнее испытывают влияние диффузии и располагаются в основном в верхних слоях, более крупные частицы под действием силы тяжести располагаются в нижних слоях. Установившееся состояние системы называют седиментационно-диффузионным равновесием. Путем подсчета частиц на двух уровнях можно определить массу и радиус частиц.

Если при установившемся седиментационно-диффузионном равновесии основная масса частиц дисперсной фазы за сравнительно короткое время окажется в осадке, систему считают кинетически (седиментационно) неустойчивой. Такая ситуация характерна для микрогетерогенных систем (суспензий, эмульсий). Если же частицы в основном остаются во взвешенном состоянии, система является кинетически (седиментационно) устойчивой. К таким системам относятся коллоидные растворы.

В реальных системах частицы обычно неоднородны по размерам, и в задачу седиментационного анализа входит опредение распределения частиц по размерам, т.е. относительного содержания различных фракций частиц (фракцией называют совокупность частиц, имеющих размеры, лежащие в определенных пределах) в полидисперсной системе.

Для проведения седиментационнго анализа кинетически устойчивых систем с целью определения размеров и массы их частиц недостаточно силы земного тяготения. Последнюю обычно заменяют более значительной центробежной силой, используя центрифуги или ультрацентрифуги.

Пример 13.2. Найти средний сдвиг 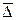при броуновском движении шарообразных частиц табачного дыма радиусом r = 10^-6 м при температуре 293 К за время 10 с. Вязкость воздуха 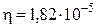Па с.

Решение. По уравнению Стокса – Энштейна находим коэффициент диффузии

.

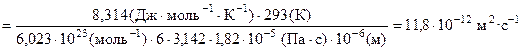По уравнению Эйнштейна – Смолуховского определяем средний сдвиг частиц

Пример 13.3. Найти скорость оседания космических частиц радиусом 4 10^-5 м на поверхности Луны. Ускорение свободного падения на Луне g _л = 1.608 м/c²; вязкость среды 10^-7 (Па с), плотность вещества частиц 3000 кг/м³.

Решение. Скорость оседания частиц находим по уравнению

Оптические свойства коллоидных растворов.

Так как частицы коллоидных систем имеют размеры не более 10^-7 м, а длина лучей видимого света находится в пределах от 4·10^-7 м (фиолетовая область) до 7 10^-7м (красная область), то в коллоидных системах наблюдается только светорассеяние, а не отражение световых лучей (как в грубодисперсных системах).

Сущность процесса светорассеяния состоит в том, что световой луч, встречая на своем пути частицу как бы огибает ее и несколько изменяет свое направление. В коллоидных растворах светорассеяние проявляется в виде опалесценции – матового свечения чаще всего голубоватых оттенков.

Теория светорассеяния была разработана Д. Рэлеем. Уравнение Рэлея для интенсивности рассеянного света I _p имеет вид:

,

где К – константа, зависящая от интенсивности падающего света и разности показателей преломления дисперсной фазы и дисперсионной среды, ν – число частиц в единице объема, V – объем частицы дисперсной, l – длина волны падающего света. На явлении светорассеяния основаны следующие методы изучения коллоидных систем:

Ультрамикроскопия: при наблюдении в микроскоп коллоидные частицы видны на темном фоне как световые точки, находящиеся в броуновском движении. Этот метод исследования коллоидных систем позволяет определить средний размер частиц и получить представление об их форме.

Нефелометрия: определяя интенсивность светорассеяния данной коллоидной системой, можно определять размер частиц и (или) концентрацию дисперсной фазы, а также изучать явления коагуляции.

Дата добавления: 2013-12-13