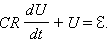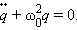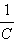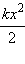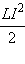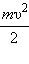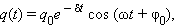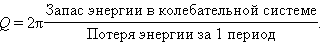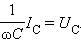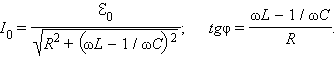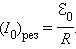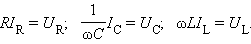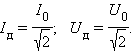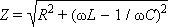Лекция 15

Глава 2. Электромагнитные колебания и волны

Глава 2. Электромагнитные колебания и волны

Глава 2. Электромагнитные колебания и волны

Глава 2. Электромагнитные колебания и волны

Колебательные и волновые процессы, изучаемые в различных разделах физики, проявляют удивительную общность закономерностей. Колебания груза на пружине и процессы в электрическом колебательном контуре, колебания столба воздуха в органной трубе и ход механических часов, распространение света и звуковых волн и т. д. – все эти явления протекают очень похожим образом. Однако, они имеют различную физическую природу. Чтобы сформулировать, например, задачу о колебаниях груза на пружине, нужно знать законы Ньютона, задача о колебаниях в электрическом контуре требует знания законов электродинамики. Но математические уравнения, описывающие процессы в этих двух системах, оказываются одинаковыми. Аналогично обстоит дело и с волновыми процессами.

Общность колебательных и волновых закономерностей проявляется в общности математических уравнений, описывающих процессы различной физической природы.

Поэтому при изучении электромагнитных колебаний и волн мы будем обращаться за аналогиями к главе «Механические колебания и волны» (часть I, гл. II).

C:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Fwd_h.gifC:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Bwd_h.gif2.1. Квазистационарные процессы. RC- и RL-цепи window.top.document.title = "2.1. Квазистационарные процессы. RC- и RL-цепи";

В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Электромагнитное поле в таких цепях состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Эти поля существуют независимо друг от друга.

Если на каком-то участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через некоторое время, которое по порядку величины равно времени τ распространения электромагнитного возмущения от одной точки цепи к другой. Так как электромагнитные возмущения распространяются с конечной скоростью, равной скорости света c, то 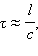где l – расстояние между наиболее удаленными точками цепи. Если это время τ много меньше длительности процессов, происходящих в цепи, то можно считать, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях называются квазистационарными.

Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи.

Из-за огромного значения скорости света время установления электрического равновесия в цепи оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные.

Простыми примерами квазистационарных процессов могут служить процессы, происходящие в RC- и RL-цепях при подключении и отключении источника постоянного тока.

На рис. 2.1.1 изображена электрическая цепь, состоящая из конденсатора с емкостью C, резистора с сопротивлением R и источника тока с ЭДС, равной .

Рисунок 2.1.1. Цепи зарядки и разрядки конденсатора через резистор.

Если замкнуть ключ K в положение 1, то начинается процесс зарядки конденсатора через резистор. По закону Ома для квазистационарной цепи можно записать:

RJ + U = ,

где J – мгновенное значение силы тока в цепи, U – мгновенное значение напряжения на конденсаторе. Сила тока I в цепи равна изменению заряда q конденсатора в единицу времени: 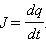Напряжение U на конденсаторе в любой момент времени равно q / C. Из этих соотношений следует

Мы получили дифференциальное уравнение, описывающее процесс зарядки конденсатора. Если конденсатор вначале не был заряжен, то решение этого уравнения имеет вид

где τ = RC – так называемая постоянная времени цепи, состоящей из резистора и конденсатора. Величина τ является характеристикой скорости процесса. При t → ∞, U(t) → . Процесс зарядки конденсатора через резистор изображен на рис. 2.1.2(I).

Рисунок 2.1.2. Зарядка (I) и разрядка (II) конденсатора через резистор.

Если после того, как конденсатор полностью зарядился до напряжения , ключ K перебросить в положение 2, то начнется процесс разрядки. Внешний источник тока в цепи разрядки отсутствует ( = 0). Процесс разрядки описывается выражением

U(t) = exp (–t / τ).

Зависимость U(t) в процессе разрядки изображена на рис. 2.1.2(II). При t = τ напряжение на конденсаторе уменьшается в e ≈ 2,7 раза.

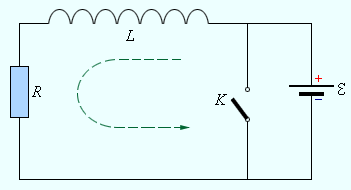
Аналогично протекают процессы в цепи, содержащей катушку с индуктивностью L и резистор с сопротивлением R (рис. 2.1.3).

Рисунок 2.1.3. Цепь, содержащая катушку с индуктивностью L, резистор с сопротивлением R и источник тока с ЭДС, равной .

Если в цепи, изображенной на рис. 2.1.3, ключ K сначала был замкнут, а затем внезапно разомкнут, то начнется процесс установления тока. Этот процесс описывается уравнением

Это уравнение по виду совпадает с уравнением, описывающим зарядку конденсатора, только теперь переменной величиной является сила тока J. Решение этого уравнения имеет вид

где постоянная времени τ = L / R. Аналогичным образом можно получить закон убывания тока в RL-цепи после замыкания ключа K:

Следует отметить, что процессы в RC- и RL-цепях аналогичны механическим процессам при движении тела в вязкой жидкости.

C:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Fwd_h.gifC:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Bwd_h.gif2.2. RLC-контур. Свободные колебания window.top.document.title = "2.2. RLC-контур. Свободные колебания";

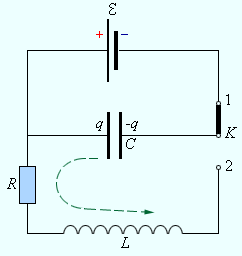
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 2.2.1).

Рисунок 2.2.1. Последовательный RLC-контур.

Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.

Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде

где 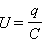– напряжение на конденсаторе, q – заряд конденсатора, 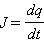– ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки. Уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду, если в качестве переменной величины выбрать заряд конденсатора q(t):

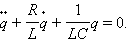
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда

(*)

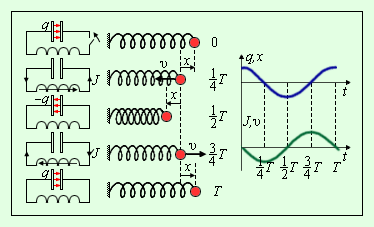
Здесь принято обозначение: 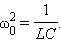Уравнение (*) описывает свободные колебания в LC-контуре в отсутствие затухания. Оно в точности совпадает по виду с уравнением свободных колебаний груза на пружине в отсутствие сил трения (ч. I, § 2.2). Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q(t) конденсатора и смещения x(t) груза от положения равновесия, а также графики тока J(t) и скорости груза υ(t) за один период 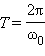колебаний.

Рисунок 2.2.2. Аналогия процессов свободных электрических и механических колебаний.

Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 1.

Электрические величины	Механические величины
Заряд конденсатора	q(t)	Координата	x(t)
Ток в цепи		Скорость
Индуктивность	L	Масса	m
Величина, обратная электроемкости		Жесткость	k
Напряжение на конденсаторе		Упругая сила	kx
Энергия электрического поля конденсатора		Потенциальная энергия пружины
Магнитная энергия катушки		Кинетическая энергия
Магнитный поток	LI	Импульс	mυ

Таблица 1.

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

q(t) = q0cos(ωt + φ0).

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний

Амплитуда q₀ и начальная фаза φ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переброса ключа K в положение 2, q₀ = Cε, φ₀ = 0.

При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:

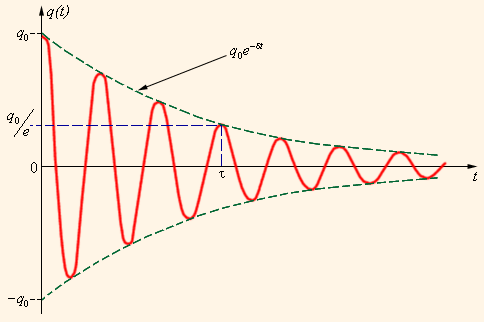
Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 2.2.3).

Рисунок 2.2.3. Затухающие колебания в контуре.

Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: F_тр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R в электрическом контуре. Уравнение свободных колебаний в контуре при наличии затухания имеет вид

(**)

Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция

которая содержит множитель exp (–δt), описывающий затухание колебаний. Скорость затухания зависит от электрического сопротивления R контура. Интервал времени в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.

В § 2.4 части 1 было введено понятие добротности Q колебательной системы:

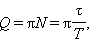
где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:

Для RLC-контура добротность Q выражается формулой

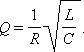
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.

Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω₀ идеального контура с теми же значениями L и C. Но при Q ≥ (5 – 10) этим различием можно пренебречь.

C:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Fwd_h.gifC:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Bwd_h.gif2.3. Вынужденные колебания. Переменный ток window.top.document.title = "2.3. Вынужденные колебания. Переменный ток";

Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями.

Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω₀.

Если частота ω₀ свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника.

Для установления стационарных вынужденных колебаний необходимо некоторое время Δt после включения в цепь внешнего источника. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи.

Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока.

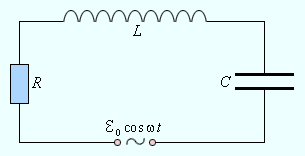
Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1):

e(t) = 0 cos ωt,

где ₀ – амплитуда, ω – круговая частота.

Рисунок 2.3.1. Вынужденные колебания в контуре.

Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому закон Ома можно записать для мгновенных значений токов и напряжений:

Величина – это перенесенная с изменением знака из правой части уравнения в левую ЭДС самоиндукции катушки. Эту величину принято называть напряжением на катушке индуктивности.

Уравнение вынужденных колебаний можно записать в виде

uR + uC + uL = e(t) = 0 cos ωt,

где u_R(t), u_C(t) и u_L(t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U_R, U_C и U_L. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм.

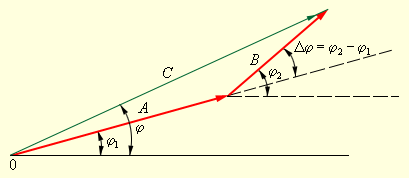
На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов (рис. 2.3.2).

Рисунок 2.3.2. Изображение гармонических колебаний A cos (ωt + φ₁), B cos (ωt + φ₂) и их суммы C cos (ωt + φ) с помощью векторов на векторной диаграмме.

Длины векторов на диаграмме равны амплитудам колебаний A и B, а наклон к горизонтальной оси определяется фазами колебаний φ₁ и φ₂. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ₁ – φ₂. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов: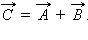

Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи.

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору емкости C и катушки индуктивности L. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.

1. Резистор в цепи переменного тока

Здесь через I_R обозначена амплитуда тока, протекающего через резистор. Связь между амплитудами тока и напряжения на резисторе выражается соотношением

RIR = UR.

Фазовый сдвиг между током и напряжением на резисторе равен нулю.

2. Конденсатор в цепи переменного тока

Соотношение между амплитудами тока I_C и напряжения U_C:

Ток опережает по фазе напряжение на угол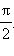

3. Катушка в цепи переменного тока

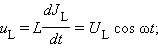
Соотношение между амплитудами тока I_L и напряжения U_L:

ωLIL = UL.

Ток отстает по фазе от напряжения на угол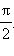

Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I₀. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги. Векторная диаграмма для последовательного RLC-контура изображена на рис. 2.3.2.

Рисунок 2.3.3. Векторная диаграмма для последовательной RLC-цепи.

Векторная диаграмма на рис. 2.3.2 построена для случая, когда 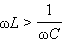или 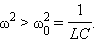В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.

Из рисунка видно, что

откуда следует

Из выражения для I₀ видно, что амплитуда тока принимает максимальное значение при условии

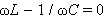
или

Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω₀ электрической цепи называется электрическим резонансом. При резонансе

Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).

При последовательном резонансе (ω = ω₀) амплитуды U_C и U_L напряжений на конденсаторе и катушке резко возрастают:

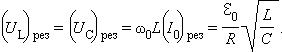
В § 2.2 было введено понятие добротности RLC-контура:

Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника.

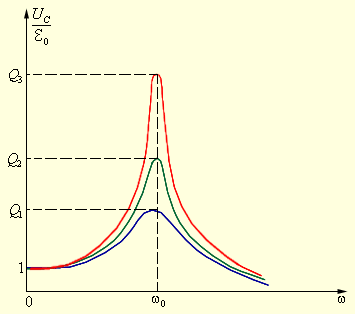
Рисунок 2.3.4. Резонансные кривые для контуров с различными значениями добротности Q.

Рис. 2.3.4 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды U_C напряжения на конденсаторе к амплитуде ₀ напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 2.3.3 называются резонансными кривыми.

Можно показать, что максимум резонансных кривых для контуров с низкой добротностью несколько сдвинуты в область низких частот.

C:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Fwd_h.gifC:\Program Files\Physicon\Open Physics 2.5 part 2\design\images\Bwd_h.gif2.4. Закон Ома для цепи переменного тока. Мощность. window.top.document.title = "2.4. Закон Ома для цепи переменного тока. Мощность.";

В § 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности:

(*)

Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений.

Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C. Физические величины R, 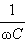и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.

При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J · u. Практический интерес представляет среднее за период переменного тока значение мощности

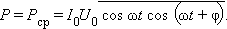
Здесь I₀ и U₀ – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0:

Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения:

Средняя мощность переменного тока на участке цепи, содержащем резистор, равна

Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением 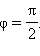Поэтому

Аналогично можно показать, что P_L = 0.

Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.

Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e(t) и током J(t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать

J(t) = I0 cos ωt; e(t) = 0 cos (ωt + φ).

Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна

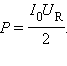Как видно из векторной диаграммы, U_R = ₀ · cos φ, поэтому Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.

В § 2.3 было выведено соотношение между амплитудами тока I₀ и напряжения ₀ для последовательной RLC-цепи:

Величину

называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде

ZI0 = 0.

(**)

Это соотношение называют законом Ома для цепи переменного тока. Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**).

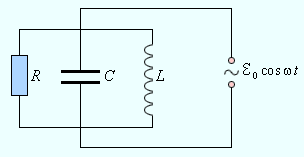
Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 2.4.1).

Рисунок 2.4.1. Параллельный RLC-контур.

При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2.

Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контура.

Из диаграммы следует:

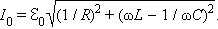
Поэтому полное сопротивление параллельного RLC-контура выражается соотношением

При параллельном резонансе (ω² = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора:

Z = Zmax = R.

Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю.

Дата добавления: 2013-12-13