Циклы напряжений. Характеристики цикла

Предисловие

Раздел 11. Усталость материалов и конструкций

Рис. 5.39

Рис. 5.38

Расчет винтовых пружин с малым шагом витков

Винтовая пружина представляет собой тонкий стержень, чаще всего круглого сечения, ось которого является винтовой линией. Винтовые пружины применяются в вагонных рессорах и различных деталях машин и механизмов. Для пружин с малым шагом витков (рис.5.38, а) соблюдается условие

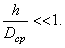(5.38)

Здесь - средний диаметр пружины, т.е. диаметр цилиндра, на котором лежит винтовая ось пружины. Таким образом, в этом случае, можно приближенно считать, что плоскость витка горизонтальна. Несмотря на сравнительную сложность формы оси, нетрудно вывести формулы для приближенного расчета пружин с малым шагом. При действии сил, направленных по оси пружины и растягивающих или сжимающих ее, стержень пружины в основном испытывает кручение.

Проведем в каком-либо месте разрез стержня пружины вертикальной плоскостью, проходящей через ось пружины (рис.5.38, б) и отбросим нижнюю часть. При условии (5.38) сечение приближенно можно считать не эллипсом, а кругом.

Действие отброшенной части на верхнюю сводится к силе Р, направленной вверх по оси пружины. При параллельном переносе силы Р в центр сечения стержня (рис.5.38, б) присоединится крутящая пара 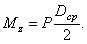Таким образом, в сечении пружины возникают два внутренних силовых фактора: поперечная сила Q=Р и крутящий момент 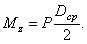Оба эти фактора вызывают в сечении касательные напряжения. Наибольшие напряжения от кручения (у контура сечения) будут равны (рис.5.38, г)

(5.39)

где d – диаметр стержня пружины.

Напряжения от поперечной силы имеют наибольшую величину вдоль горизонтального диаметра АВ сечения, где они направлены вертикально. По формуле Журавского (рис.5.38, в)

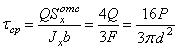. (5.40)

Внутренняя точка А диаметра является опасной точкой сечения, так как здесь напряжения 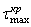и совпадают по направлению и складываются. Расчетное напряжение будет

(5.41)

При малом отношении 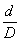можно вторым членом в скобках пренебречь по сравнению с единицей, т.е. рассчитывать пружину на одно кручение.

Если же отношение 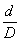не мало (например, в вагонных рессорах и других тяжелых пружинах), то влияние поперечной силы на напряжения значительно и должно учитываться. Кроме того, в этом случае существенно сказывается влияние кривизны стержня пружины, вследствие которой напряжение от кручения у внутренней точки А сечения оказывается больше, чем у наружной точки В. Ввиду этого в правую часть формулы (5.41) вместо выражения, стоящего в скобках, лучше ввести коэффициент К, учитывающий одновременно влияние поперечной силы и кривизны стержня:

(5.42)

Этот коэффициент можно вычислять по формуле

(5.43)

где - геометрический параметр пружины.

На практике нужно уметь вычислять удлинение или осадку пружины от растягивающих или сжимающих ее сил. Влияние поперечной силы на удлинение невелико, поэтому обычно принимается в расчет влияние кручения витков.

На рис.5.39 показан бесконечно малый элемент проволоки пружины , находящейся в условиях кручения. Правое сечение поворачивается на угол

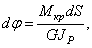
а все точки на оси перемещаются на величину

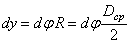. (5.44)

Суммируя эти перемещения за счет закручивания длины проволоки, получим полное сокращение расстояния между торцами пружины

(5.45)

Условие прочности пружины

(5.46)

Так как пружины должны давать достаточно большие упругие удлинения, то они изготовляются из закаленной стали с очень высоким пределом пропорциональности. Допускаемое касательное напряжение 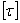колеблется при статической нагрузке от 350 МПа до 500 МПа, а для особо прочных специальных сталей – и выше. При переменной нагрузке допускаемое напряжение значительно снижается (на 30-65%).

Первые наблюдения усталостного разрушения относятся к концу XVIII века, когда у длительно эксплуатируемых дилижансов в Англии и почтовых карет во Франции неожиданно для инженерного мира стали хрупко ломаться оси, изготовленные из кованого железа, обладающего высокой пластичностью. Специалисты того времени объясняли это явление перерождением материала за счет его усталости в процессе длительной эксплуатации под действием переменных напряжений, возникающих из-за неровностей дороги. С тех пор термин "Усталость материалов", хотя не отражающий полностью сложные процессы, протекающих в металле под воздействием напряжений, переменных во времени, нашёл высокое распространение в инженерных методах расчёта надёжности элементов конструкций.

Первые систематические экспериментальные исследования сопротивления усталостному разрушению стальных образцов при действии переменных нагрузок были проведены немецким ученым А. Велером, который опубликовал результаты исследований в виде итоговых таблиц в 1870 г. Графическое представление этих результатов в виде кривых усталости впервые было осуществлено Л. Шпангенбергом в 1875 г., хотя в мировой практике эти кривые связываются только с именем А. Велера.

Усталость материалов и в настоящее время является одной из основных причин отказа деталей машин и элементов конструкции, подверженных действию напряжений, циклически изменяющихся во времени. В связи с этим для повышения ресурса и надежности подобных конструкций важное значение приобретают вопросы выбора материала, обоснования режимов технологии производства полуфабрикатов и деталей и организации контроля технологического процесса, обеспечивающие стабильное и высокое сопротивление элементов конструкций усталостному разрушению.

Решения проблемы повышения ресурса и надёжности машин обусловливает разработку и внедрение вероятностных методов расчёта на прочность при переменных напряжениях, учитывающих случайный характер действующих нагрузок и вариацию характеристик сопротивления усталости материалов и деталей.

Характеристики сопротивления усталостному разрушению материала и изделий определяются в результате испытаний на усталость образцов, моделей, натурных деталей и конструкций в целом, что требует больших материальных затрат и весьма длительного времени, которого, как правило, не хватает конструктору на стадии проектирования и доводки конструкции. В связи с этим ученые многих стран ведут поиски расчётных (косвенных) методов оценки характеристик сопротивления усталостному разрушению и методов ускоренных и форсированных испытаний на усталость.

1. Характеристики сопротивления усталости конструкционных материалов, используемые в расчётах на прочность при многоцикловом нагружении

В данном разделе рассматриваются основные характеристики сопротивления усталости материалов и деталей, термины, определения и обозначения, применяемые в науке и технике, в соответствии с ГОСТ 23207—78.

Совокупность последовательных значений напряжений за один период их изменения при регулярном нагружении (рис.1.1) называется циклом напряжений.

Характеристики цикла напряжений.

Частота циклов f — отношение числа циклов напряжений к интервалу времени их действия.

Период цикла Т – продолжительность одного цикла напряжений, T= 1 /f (рис.1.1.)

Максимальное напряжение цикла 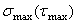— наибольшее по алгебраическому значению напряжение цикла (рис. 1.1., рис. 1.2.)

Минимальное напряжение цикла — наименьшее по алгебраическому значению напряжение цикла (рис.1.1, 1.2).

Среднее напряжение цикла — постоянная (положительная или отрицательная) составляющая цикла напряжений (рис.1.1, 1.2), равная алгебраической полусумме максимального и минимального напряжения цикла,

;

Амплитуда напряжений цикла 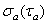— наибольшее числовое положительное значение переменной составляющей цикла напряжений (рис.1.1., рис.1.2.), равная алгебраической полуразности максимального и минимального напряжения цикла

;

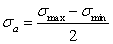Размах напряжений цикла 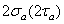— алгебраическая разность максимального и минимального напряжения цикла, , .

Коэффициент асимметрии цикла напряжений , отношение минимального напряжения цикла к максимальному,

;

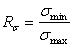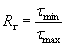
Дата добавления: 2013-12-13