Эмпирический метод

Эмпирический метод оценки коэффициента чувствительности материала к асимметрии цикла напряжений заключается в статистическом обобщении накопленных в отечественной и зарубежной практике результатов экспериментов по отдельным близким группам конструкционных материалов.

Так, например, в ныне действующем стандарте [14] и работе [8] рекомендуется формула для расчетов 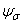применительно к сталям

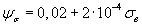, (2.65)

где 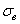в МПа.

Следует отметить, что формула (2.65) противоречит опытным данным и, как будет показано ниже (формула (2.76)), теоретическим расчетам. Корреляционный и регрессионный анализ опытных данных отечественных и зарубежных исследователей (рис. 2.8) указывает на убывание величины коэффициента чувствительности асимметрии цикла с ростом статической прочности сталей. Коэффициент корреляции между наблюдаемыми в экспериментах значениям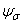и и 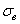оказался отрицательным и равным r = -0.28, что говорит о снижении чувствительности асимметрии цикла напряжений с ростом статической прочности сталей [15].

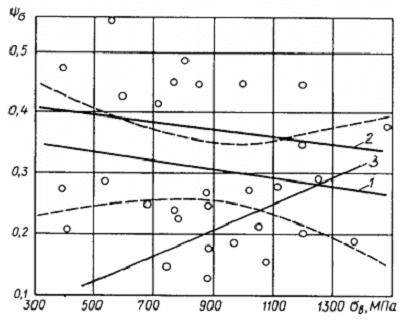
Рис. 2.8. Зависимости коэффициента 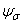сталей от предела прочности:
1- линия регрессии [уравнение (2.66)]; 2- расчет по формуле (2.76); 3- расчет по формуле (2.65); o — экспериментальные значения; штриховые линии – границы 95% -ой доверительной области.

Уравнение эмпирической линии регрессии для сталей по результатам, представленным на рис. 2.8, имеет вид

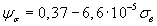. (2.66)

Статистическому анализу было подвержено 30 вариантов марок сталей и их состояний.

Большой разброс экспериментальных значений 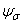, связанный с упомянутым ранее малым объемом испытаний на каждую кривую усталости (8...10 образцов), при сравнительно ограниченным объеме выборке (30 вариантов сталей) определили высокую меру индивидуального рассеяния вокруг линии регрессии 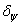= 0.11 и весьма широкую 95%-ную доверительную область линии регрессии.

В связи с этим формулой (2.66) можно пользоваться только для приблизительной оценки 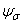. Для повышения точности этой формулы следует привлечь к статистическому анализу дополнительные экспериментальные данные, доведя объем выборки до 100...150 вариантов сталей и их состояний, что в настоящее время представляется трудно выполнимой задачей.

Экспериментальные данные для 30 вариантов алюминиевых сплавов, представлены на рис. 2.9. Коэффициент корреляции между коэффициентов чувствительности к асимметрии 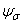для базы N = 10⁷ циклов и пределом прочности тоже оказался отрицательным и равным r = - 0.23. Индивидуальная мера рассеяния вокруг линии регрессии достигает 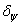= 0,14, что соответствует средней квадратической ошибке оценки по корреляционному уравнению (40...60%).

Однако, осреднение 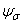по ряду баз испытания позволяет снизить указанную ошибку в 2 раза. В этом случаи, корреляционное уравнение имеет вид [1, 10, 11]

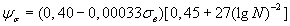, (2.67)

где N — база испытания.

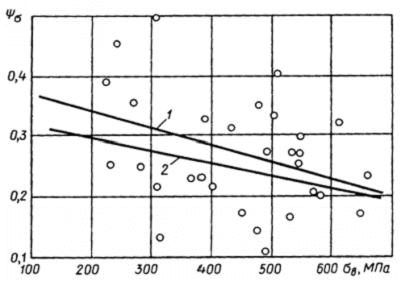
Рис.2.9. Зависимости коэффициента 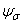алюминиевых сплавов от предела прочности: 1 - линия регрессии [уравнение (2.67)]; 2 - расчет по формуле (2.78); o - экспериментальные значения

Таким образом, экспериментальный и эмпирический подходы к оценке величины коэффициента чувствительности материала к асимметрии нагружения не являются надежными.

Дата добавления: 2013-12-13