
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ускоренный метод оценки дисперсии предела выносливости
|
|
|
|
Другую возможность оценки характеристик рассеяния усталостных свойств материалов и элементов конструкций дают результаты испытаний на усталость с возрастающей амплитудой цикла напряжений. Для этой цели при постоянной скорости возрастания амплитуды испытывают серию из n образцов и вычисляют выборочное значение среднего и дисперсию разрушающей амплитуды цикла напряжений по формулам
 (4.21)
(4.21)
и
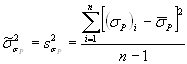 (4.22)
(4.22)
Проведенный автором [1, 25] статистический анализ результатов массовых испытаний на усталость литейных и деформируемых магниевых и алюминиевых сплавов (таблица 4.4) показал, что дисперсия разрушающих амплитуд не зависит скорости нагружения.
Уровни значимости критерия Бартлета [4] о равенстве генеральных дисперсий разрушающих амплитуд для всех рассмотренных скоростей нагружения не опускаются ниже 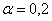 . Впоследствии эта закономерность была подтверждена [21] и для сплавов на железной основе.
. Впоследствии эта закономерность была подтверждена [21] и для сплавов на железной основе.
Уровень начального значения амплитуды цикла напряжения также не оказывает заметного влияния на дисперсию разрушающих напряжений. Так, применение критерия Фишера [4] о равенстве генеральных дисперсий разрушающих амплитуд цикла напряжений для двух значений уровней начальной амплитуды (таблица 4.4) показывает, что отношение выборочных дисперсий незначимо отличается от единицы. Например, для сплава АД35 - F = 1.26, в то время как для уровня значимости 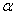 =0.05 критическое значение критерия
=0.05 критическое значение критерия 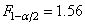 ; для сплава типа АВ с 0,6% Mn и 0,01% Cu - F = 1,10 при
; для сплава типа АВ с 0,6% Mn и 0,01% Cu - F = 1,10 при  и для сплава типа АВ с 0.12% Mn и 0.04% Cu - F = 1,02 при
и для сплава типа АВ с 0.12% Mn и 0.04% Cu - F = 1,02 при 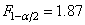 .
.
Независимость дисперсии разрушающих амплитуд цикла напряжений от уровня начальной амплитуды и скорости возрастания напряжений дает возможность оценки обобщенной дисперсии путем объединения дисперсий для различных скоростей и уровней начальной амплитуды
 , (4.23)
, (4.23)
где 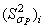 — дисперсия разрушающих амплитуд цикла напряжений при скорости αi возрастания амплитуды, подсчитывается по формуле (4.22); m — число вариантов скоростей возрастания амплитуды для всех значений уровней начального напряжения; ni — число испытанных образцов при скорости αi.
— дисперсия разрушающих амплитуд цикла напряжений при скорости αi возрастания амплитуды, подсчитывается по формуле (4.22); m — число вариантов скоростей возрастания амплитуды для всех значений уровней начального напряжения; ni — число испытанных образцов при скорости αi.
Анализ и сопоставление результатов обычных испытаний на усталость и испытаний с возрастающей амплитудой цикла напряжений, а также структура уравнения (3.1), дают основания считать, что дисперсия предела выносливости 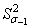 равна дисперсии разрушающих амплитуд цикла напряжений
равна дисперсии разрушающих амплитуд цикла напряжений  , то есть
, то есть
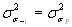 (4.24)
(4.24)
Таблица 4.4. Результаты ускоренных испытаний с возрастающей амплитудой цикла напряжений образцов из легких сплавов
| Сплав | 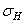 , МПа , МПа
| 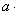 104, МПа/цикл 104, МПа/цикл
| n |  , МПа , МПа
|  , (МПа)2 , (МПа)2
| Обобщенная (осредненная) дисперсия, 
| ||||
по скорости 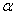
| по скорости 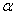 и уровню начального напряжения и уровню начального напряжения 
| |||||||||
| Магниевый сплав МЛ5 | 0,4 2,0 6,0 | 20 20 15 | 81,8 99,9 115,5 | 133,0 143,2 129,3 | 135,6 | 135,6 | ||||
| Алюминиевый сплав АД35 | 0,34 0,87 1,70 2,56 3,34 6,68 | 20 20 20 20 20 10 | 178,1 194,7 204,0 218,2 227,9 247,6 | 108,2 41,5 58,2 95.0 129,5 85,0 | 86,3 | 90,9 | ||||
| 0,34 1,70 3,34 | 10 10 10 | 168,1 193,9 211,3 | 102,1 46,3 169,2 | 108,6 | ||||||
| Алюминиевый сплав типа АВ (Cu – 0,46%, Mn – 0,25%) | 0,332 1,66 3,32 6,64 | 25 20 20 10 | 184,8 217,2 238,5 258,6 | 115,6 87,5 100,0 144,0 | 107,9 | 107,9 | ||||
| Алюминиевый сплав типа АВ (Cu – 0,01%, Mn – 0,6%) | 0,332 0,87 1,66 3,32 6,64 | 10 10 10 10 10 | 172,1 181,1 194,4 210,4 225,4 | 36,6 40,1 42,3 55,3 55,0 | 45,4 | 47,5 | ||||
| 0,332 0,87 1,70 3,32 6,64 | 5 10 5 10 10 | 161,8 176,1 185,6 208,2 216,7 | 24,7 53,7 51,1 47,3 60,0 | 50,1 | ||||||
| Алюминиевый сплав типа АВ (Cu – 0,095%, Mn – 0,28%) | 0,332 0,87 1,70 3,32 6,64 | 10 10 10 10 10 | 167,8 180,8 192,3 207,2 225,0 | 50,0 31,4 35,1 31,8 35,8 | 36,9 | 36,9 | ||||
| Алюминиевый сплав типа АВ (Cu – 0,04%, Mn – 0,12%) | 0,332 1,83 6,64 | 10 10 10 | 165,0 194,4 231,8 | 54,0 65,4 43,8 | 54,3 | 54,7 | ||||
| 0,332 1,83 6,64 | 10 10 10 | 161,2 191,0 227,5 | 52,1 53,6 59,6 | 55,1 | ||||||
Условные обозначения:
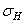 - начальный уровень амплитуды цикла напряжений;
- начальный уровень амплитуды цикла напряжений; 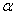 - скорость возрастания амплитуды; n — число испытанных образцов;
- скорость возрастания амплитуды; n — число испытанных образцов; 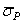 - выборочное среднее значение амплитуды разрушающих напряжений;
- выборочное среднее значение амплитуды разрушающих напряжений;  - выборочная дисперсия амплитуды разрушающих напряжений;
- выборочная дисперсия амплитуды разрушающих напряжений; 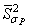 - обобщенная (осредненная) дисперсия амплитуды разрушающих напряжений.
- обобщенная (осредненная) дисперсия амплитуды разрушающих напряжений.
Для легких сплавов эта дисперсия соответствует базе N = 107 циклов. Для других баз испытания дисперсию предела выносливости алюминиевых сплавов с учетом инвариантности его коэффициента вариации к базе и уравнения (2.38) подсчитывают по формуле
 , (4.25)
, (4.25)
а для титановых сплавов с учетом (2.43)
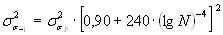 . (4.26)
. (4.26)
Изложенная методика ускоренной оценки дисперсии предела выносливости и рассмотренный ранее способ расчета медианы или среднего значения предела выносливости позволяют оценить коэффициент вариации этой характеристики сопротивления усталости
 , (4.27)
, (4.27)
который (на основании уравнений (4.17)...(4.20)) открывает возможность расчета среднего квадратического отклонения логарифма долговечности на любом участке кривой усталости.
Представление о точности оценки характеристик рассеяния усталостных свойств на основании результатов ускоренных испытаний с возрастающей амплитудой цикла напряжений дает таблица 4.5, где сопоставлены итоги использования ускоренного и обычного методов испытаний на усталость для литейного магниевого сплава МЛ5 и деформируемого алюминиевого сплава АВ.
Таблица 4.5. Сопоставление характеристик рассеяния предела выносливости образцов из легких сплавов МЛ5 и АВ, определенных по результатам ускоренного и обычного методов испытаний
| Характеристика | Метод определения | Сплав АВ | Сплав МЛ5 | ||
| N =107 | N =5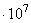
| N =108 | N =107 | ||
| Медиана предела выносливости в МПа | Ускоренный | ||||
| Обычный | |||||
| Расхождение в % | +4,4 | +4,2 | +6,2 | -6,0 | |
| Среднее квадратическое отклонение предела выносливости в МПа | Ускоренный | 10,4 | 9,2 | 8,8 | 11,6 |
| Обычный | 10,7 | 9,4 | 8,9 | 10,5 | |
| Расхождение в % | -2,8 | -2,1 | -1,1 | +10,5 | |
| Коэффициент вариации предела выносливости | Ускоренный | 0,074 | 0,074 | 0,073 | 0,184 |
| Обычный | 0,079 | 0,079 | 0,079 | 0,157 | |
| Расхождение в % | -6,3 | -6,3 | -7,6 | +17,2 |
Анализ результатов, приведенных в таблице 4.5, показал, что рассмотренная методика ускоренной оценки дисперсии предела выносливости дает вполне удовлетворительные результаты. Аналогичные результаты были получены и для других сплавов, а также для натурных элементов конструкций [20].
Вопросам планирования испытаний на усталость, в том числе и ускоренных, посвящены работы Агамирова Л.В. [23, 26, 27 и др.], в которых даны оценки погрешностей определения усталостных характеристик в зависимости от объема и методики испытаний. Применительно к испытаниям, рассмотренным в настоящем разделе, показано, что относительная средняя квадратическая ошибка оценки среднего квадратического отклонения предела выносливости в долях этого отклонения определяется из приближенного асимптотического уравнения
 , (4.28)
, (4.28)
которое может быть использовано для определения необходимого объема ускоренных испытаний на усталость с целью оценки среднего квадратического отклонения предела выносливости с погрешностью, не превышающей 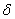 , то есть
, то есть
 . (4.29)
. (4.29)
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 292; Нарушение авторских прав?; Мы поможем в написании вашей работы!