Центр тяжести маятника совпадает с его центром масс

Точка подвеса маятника - точка О пересечения оси качания маятника и перпендикулярной оси качания.

Уравнение его движения запишем в виде:

.

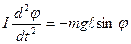В случае малых колебани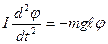й , или 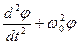=0, где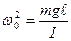

Это уравнение движения тела, совершающего гармонические колебания.

Частота колебаний физического маятника зависит от его массы, длины и момента инерции относительно оси, проходящей через точку подвеса.

Обозначим .

Величина называется приведённой длинной физического маятника - это длина математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведённой длины от оси вращения, называется центром качания физического маятника (О’).

Если маятник подвесить в центре качания, то приведённая длина и период колебаний будут теми же, что и в точке О.

Таким образом, точка подвеса и центр качания обладают свойствами взаимности: при переносе точки подвеса в центр качения прежняя точка подвеса становится новым центром качения.

Период колебания:

Математический маятник, который качается с таким же периодом, как и рассматриваемый физический, называется изохронным данному физическому маятнику.

Общие выводы. Рассмотренные примеры

· относятся к свободным колебаниям без трения, которые происходят в системе, предоставленной самой себе после того, как она была тем илииным способом выведена из состояния равновесия.

· свободные колебания любого осциллятора в отсутствие трения будут гармоническими, если действующая внем сила (или момент силы) является квазиупругой, т. е. силой, направленной к положению равновесия и зависящей от смещения из этого положения линейно.

· квазиупругий характер силы (или момента силы)служит и критерием малых колебаний.

· частота и период свободных колебаний без трения зависят только от свойств самого осциллятора.

· Амплитуда колебаний и начальная фаза определяются начальными условиями.

Рассмотрим еще один пример на малые колебания.

Пример. Частица массы т совершает колебания в силовом поле, где ее потенциальная энергия зависит от координаты х как где U₀ и α — постоянные. Найдем частоту ω₀ малых колебаний частицы около положения равновесия х = 0.

Согласно основному уравнению динамики,

/

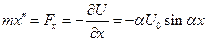Так как колебания малые, то 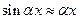и предыдущее уравнение можно привести к виду

/

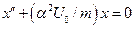Отсюда следует, что .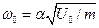

Дата добавления: 2013-12-13